Calculadora de Cotangente (Graus e Radianos)
Resultado:
Gráfico de cotangente
Com esta calculadora, você pode obter a cotangente de qualquer ângulo inserido. Você pode usar graus, radianos e π radianos. Ao inserir um ângulo, a calculadora exibirá sua cotangente imediatamente.
Abaixo você pode encontrar informações adicionais sobre como usar a calculadora cotangente. Além disso, você também pode aprender sobre a definição, gráfico e valores importantes da cotangente.
Como usar a calculadora de cotangente?
Passo 1: Comece selecionando o tipo de ângulo que deseja usar. Ao clicar no botão azul, você poderá selecionar entre graus, radianos e π radianos.
Passo 2: Insira o ângulo na caixa correspondente. É possível usar ângulos positivos e negativos.
Passo 3: A cotangente do ângulo inserido será exibida no painel direito.
Diferença entre usar graus, radianos e π radianos na calculadora
Para encontrar a relação entre graus e radianos, podemos lembrar que uma revolução completa tem um total de 360° ou 2π radianos. Isso significa que 180° é equivalente a π radianos.
A diferença entre π radianos e radianos, por outro lado, é simplesmente que, usando “π radianos” na calculadora, estaremos multiplicando qualquer valor inserido por π. Por exemplo, se inserirmos 1,5, estaremos calculando a cotangente de 1,5π radianos.
Assim, podemos inserir 0,5π na calculadora, selecionando a opção “π radianos” e simplesmente inserindo 0,5. No entanto, também podemos selecionar a opção “radianos” e inserir 1,571, que equivale a 0,5π, pois π tem um valor de aproximadamente 3,1415…
O que é cotangente de um ângulo?
A cossecante é a função recíproca da cotangente. Isso significa que a cotangente é igual a 1 sobre a tangente de um ângulo. Considerando que a tangente é igual a seno sobre cosseno, a cotangente é igual a cosseno sobre seno.
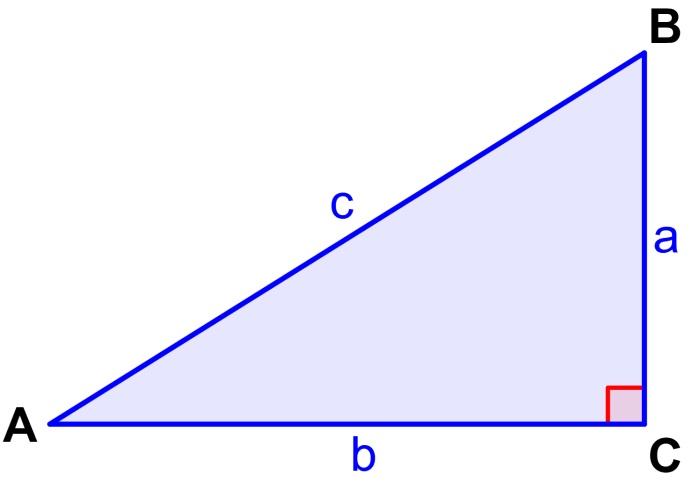
Além disso, também podemos definir a cotangente em relação aos lados de um triângulo retângulo. Fazendo isso, temos que a cotangente de um ângulo é igual ao comprimento do lado adjacente ao ângulo dividido pelo comprimento do lado oposto ao ângulo.
Por exemplo, no triângulo retângulo a seguir, podemos definir a cotangente do ângulo A como o comprimento do lado b (lado adjacente ao ângulo A) dividido pelo comprimento do lado a (lado oposto ao ângulo A).
Da mesma forma, podemos definir a cotangente do ângulo B como o comprimento do lado a (lado adjacente ao ângulo B) dividido pelo comprimento do lado b (lado oposto ao ângulo B).
Se você quiser saber mais sobre a cotangente de um ângulo, acesse nosso artigo Cotangente de um ângulo – Fórmulas e exercícios.
Por que a Cotangente de 0° e 180° é indefinida?
A função cotangente é a recíproca da tangente e será indefinida quando a tangente de um ângulo for igual a 0. Isso porque não podemos ter denominadores iguais a 0.
Como a cotangente pode ser definida como cosseno sobre o seno do ângulo, ela será indefinida sempre que o seno do ângulo for igual a 0. Isso acontece quando temos um ângulo de 0.
Além disso, como a função seno é periódica, esse valor se repete toda vez que adicionamos 180°n, onde n é qualquer número inteiro positivo ou negativo.
Por exemplo, o seno de 0°+180°(2)=360°, também é igual a 0, então a cotangente de 360° é indefinida.
Gráfico da cotangente de um ângulo
A cotangente pode ser representada graficamente considerando os ângulos que estão fora de um triângulo retângulo. Ou seja, podemos usar ângulos positivos e negativos maiores que 180°.
A função cotangente é periódica. Isso significa que seu gráfico se repete após um intervalo fixo. O período da função cotangente é igual a 180° ou π radianos.
Domínio da cotangente de um ângulo
Podemos usar o gráfico da cotangente para encontrar seu domínio. A partir do gráfico, podemos deduzir que a função se estende do infinito negativo ao infinito positivo.
No entanto, a função cotangente tem assíntotas, nas quais a função se aproxima do infinito e se torna indefinida. As assíntotas estão localizadas a cada 180° a partir de 0. Assim, o domínio da cotangente são todos os números reais, exceto 180°n ou πn, onde n é um inteiro positivo ou negativo.
Imagem da cotangente de um ângulo
No gráfico da cotangente, podemos ver que a função pode resultar em qualquer valor, tanto positivo quanto negativo. Não temos restrições na imagem.
Portanto, a imagem da cotangente é igual a todos os números reais.
Tabela da cotangente de ângulos comuns
| Graus | Radianos | Cotangente |
| 90° | 0 | |
| 60° | ||
| 45° | 1 | |
| 30° | ||
| 0° | 0 | Indefinido |
Calculadoras relacionadas:
- Calculadora de Cosseno (Graus e Radianos)
- Calculadora de Seno (Graus e Radianos)
- Calculadora de Tangente (Graus e Radianos)
- Calculadora de Secante (Graus e Radianos)
- Calculadora de Cossecante (Graus e Radianos)
Você pode explorar outras calculadoras aqui.