Calculadora de Cosseno (Graus e Radianos)

Resultado:

–

Gráfico de cosseno

Esta calculadora permite encontrar o cosseno de um ângulo inserido. Ao inserir um ângulo, a calculadora exibirá imediatamente o valor de seu cosseno. Você pode usar graus e radianos.

Abaixo você pode encontrar informações importantes relacionadas ao cosseno. Você encontrará a definição de cosseno, seu gráfico com as características mais fundamentais e os valores de cosseno de ângulos importantes.

Como usar a calculadora de cosseno?

Passo 1: Selecione o tipo de ângulo que deseja inserir. Clique no botão azul para selecionar entre usar graus, radianos ou π radianos.

Passo 2: Insira o ângulo na caixa correspondente. Você pode usar números positivos e negativos.

Passo 3: O cosseno do ângulo inserido será exibido no painel direito.

Qual é a diferença entre graus, radianos e π radianos na calculadora?

Uma revolução completa é igual a 360° ou 2π radianos. Isso significa que 180° é equivalente a π radianos.

Além disso, π é uma constante que indica a razão entre o diâmetro e a circunferência de um círculo. Seu valor aproximado é 3,1415… Assim, π radianos é aproximadamente 3,1415 radianos.

Suponha que queremos inserir o ângulo de 45°. Na calculadora, temos as seguintes opções:

Podemos selecionar “graus” e inserir 45.
Podemos selecionar “π radianos” e inserir 0,25 (180° é igual a π radianos, então 45° é igual a 1/4 π radianos).
Podemos selecionar “radianos” e inserir 0,7854 (0,25π radianos é igual a 0,7854 radianos).

O que é cosseno de um ângulo?

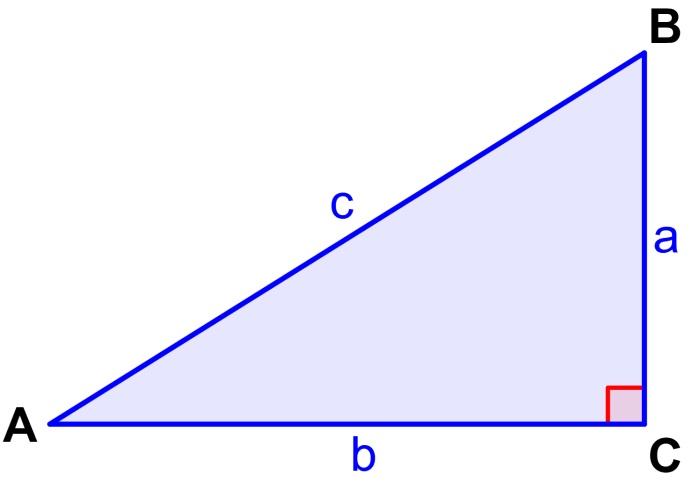
O cosseno de um ângulo pode ser definido referindo-se a um triângulo retângulo. Assim, o cosseno é igual ao comprimento do lado adjacente ao ângulo dividido pelo comprimento da hipotenusa do triângulo.

Por exemplo, no triângulo retângulo a seguir, o cosseno do ângulo A é igual ao comprimento do lado b (lado adjacente a A) dividido pelo comprimento do lado c (hipotenusa e oposto ao ângulo reto).

Da mesma forma, o cosseno do ângulo B é igual ao comprimento do lado a (lado adjacente a B) dividido pelo comprimento do lado c (hipotenusa).

Se você quiser saber mais sobre o cosseno de um ângulo, acesse nosso artigo Cosseno de um ângulo – Fórmulas e exercícios.

Gráfico do cosseno de um ângulo

Embora o cosseno seja definido usando um triângulo retângulo, sua definição pode ser estendida para abranger ângulos que vão além dos ângulos encontrados em um triângulo.

O cosseno é uma função periódica, o que significa que se repete após um intervalo fixo. Neste caso, a função cosseno se repete a cada 360° ou 2π.

Domínio do cosseno de um ângulo

Usando o gráfico de cosseno, podemos facilmente deduzir que a função cosseno pode receber qualquer valor de entrada (geralmente valores x) tanto positivos quanto negativos. Portanto, o domínio do cosseno é igual a todos os números reais.

Imagem do cosseno de um ângulo

Usando o gráfico de cosseno, podemos ver que os valores de saída da função variam de -1 a 1. Isso significa que a imagem da função cosseno é igual a -1 ≤ cos(α) ≤ 1.

Tabela de cossenos de ângulos comuns

Graus	Radianos	Cosseno
180°	π	-1
150°	5π/6	-√3/2
135°	3π/4	-√2/2
120°	2π/3	-1/2
90°	π/2	0
60°	π/3	1/2
45°	π/4	√2/2
30°	π/6	√3/2
0°	0	1

Calculadoras relacionadas:

Você pode explorar outras calculadoras aqui.