Sistemas de equações são equações simultâneas que compartilham as mesmas soluções. Podemos resolver sistemas de duas equações com duas incógnitas usando o método de substituição. Este método consiste em isolar uma das variáveis em uma das equações. Depois, precisamos substituir essa expressão na segunda equação para formar uma única equação com uma incógnita.
A seguir, aprenderemos como resolver sistemas de equações usando o método da substituição. Vamos resolver vários exercícios para entender o processo utilizado.
ÁLGEBRA
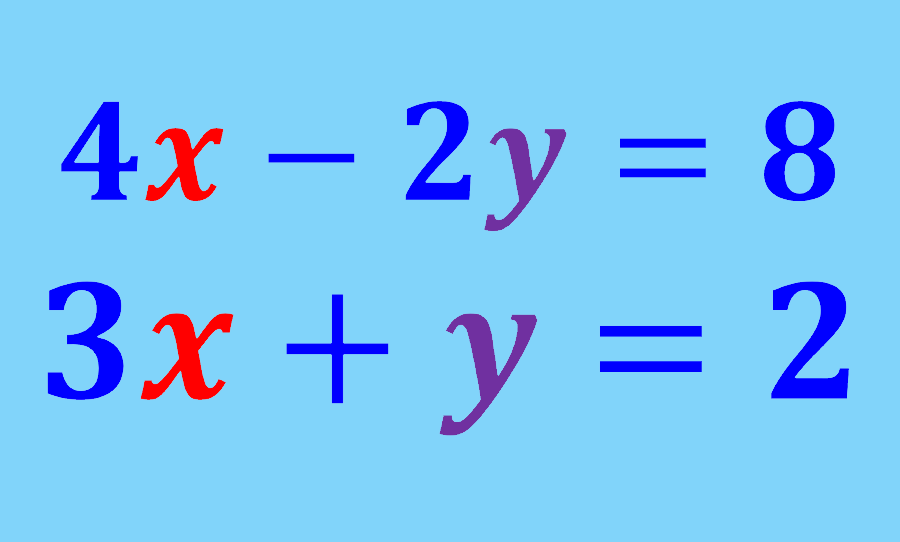
Relevante para…
Aprender a resolver sistemas de equações com o método da substituição.
ÁLGEBRA
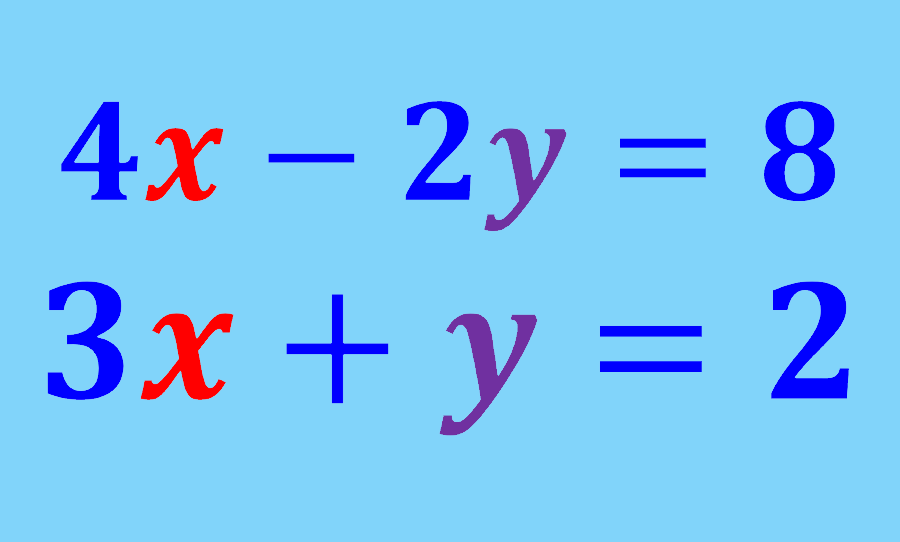
Relevante para…
Aprender a resolver sistemas de equações com o método da substituição.
Passos para resolver sistemas de equações por substituição
O método da substituição para resolver sistemas de equações consiste em resolver uma das equações para uma das variáveis. Em seguida, substituímos a expressão obtida na segunda equação e obteremos uma equação com uma única variável, que pode ser facilmente resolvida.
Em detalhes, podemos seguir os seguintes passos para resolver sistemas de equações por substituição:
1. Simplifique ambas as equações, se possível.
Isso inclui remover parênteses, combinar termos semelhantes e eliminar frações.
2. Resolva uma equação para uma variável.
Podemos escolher qualquer uma das equações e resolver qualquer uma das variáveis.
3. Substitua a expressão obtida no passo 2 na outra equação.
Ao fazer isso, obteremos uma equação com apenas uma incógnita.
4. Resolva a equação do passo 3.
Fazendo isso, obteremos o valor de uma das variáveis. Se você precisar revisar, pode dar uma olhada em nosso artigo sobre como resolver equações com uma incógnita.
5. Encontre o valor da outra variável.
Substituímos o valor da variável obtida no passo 4 em qualquer uma das duas equações e resolvemos.
Sistemas de equações por substituição – Exercícios resolvidos
EXERCÍCIO 1
Encontre as soluções para o sistema de equações usando o método da substituição: $latex \begin{cases}x+2y=10 \\ 2x-y=5 \end{cases}$
Solução
Passo 1: As equações já estão simplificadas.
Passo 2: Resolvendo a primeira equação para x, temos:
$latex x+2y=10$
$latex x=10-2y$
Passo 3: Substituindo $latex por x=10-2y$ na segunda equação, temos:
$latex 2x-y=5$
$latex 2(10-2y)-y=5$
$latex 20-4y-y=5$
Passo 4: Resolvendo para y, temos:
$latex 20-4y-y=5$
$latex -5y=-15$
$latex y=3$
Passo 5: Substituindo o valor $latex y=3$ na primeira equação, temos:
$latex x+2y=10$
$latex x+2(3)=10$
$latex x=4$
A solução para o sistema é $latex x=4,~~y=3$.
EXERCÍCIO 2
Resolva o seguinte sistema de equações usando o método da substituição: $latex \begin{cases}-2x-y=1 \\ 3x+4y=6 \end{cases}$
Solução
Passo 1: As equações já estão simplificadas.
Passo 2: Resolvendo a primeira equação para y, temos:
$latex -2x-y=1$
$latex -y=1+2x$
$latex y=-1-2x$
Passo 3: Substituindo $latex y=-1-2x$ na segunda equação, temos:
$latex 3x+4y=6$
$latex 3x+4(-1-2x)=6$
$latex 3x-4-8x=6$
Passo 4: Resolvendo para x, temos:
$latex 3x-4-8x=6$
$latex -5x=10$
$latex x=-2$
Passo 5: Substituindo $latex x=-2$ na primeira equação, temos:
$latex -2x-y=1$
$latex -2(-2)-y=1$
$latex 4-y=1$
$latex -y=-3$
$latex y=3$
A solução do sistema é $latex x=-2, ~~y=3$.
EXERCÍCIO 3
Encontre a solução para o sistema de equações usando o método da substituição: $latex \begin{cases}2(2x-4)+y=3 \\ -x+2y=4 \end{cases}$
Solução
Passo 1: Podemos simplificar a primeira equação:
$latex \begin{cases}4x-8+y=3 \\ -x+2y=4 \end{cases}$
Passo 2: Resolvendo a primeira equação para y, temos:
$latex 4x-8+y=3$
$latex y=-4x+11$
Passo 3: Substituindo $latex y=-4x+11$ na segunda equação, temos:
$latex -x+2y=4$
$latex -x+2(-4x+11)=4$
$latex -x-8x+22=4$
Passo 4: Resolvendo para x, temos:
$latex -x-8x+22=4$
$latex -9x=-18$
$latex x=2$
Passo 5: Substituindo $latex x=2$ na segunda equação, temos:
$latex -x+2y=4$
$latex -2+2y=4$
$latex 2y=6$
$latex y=3$
A solução do sistema é $latex x=2,~~y=3$.
EXERCÍCIO 4
Resolva o sistema de equações: $latex \begin{cases}3x+4y-27=0 \\ 5x+y-11=0 \end{cases}$
Solução
Passo 1: As equações já estão simplificadas.
Passo 2: Podemos resolver a segunda equação para y:
$latex 5x+y-11=0$
$latex y=-5x+11$
Passo 3: Substituindo $latex y=-5x+11$ na primeira equação, temos:
$latex 3x+4y-27=0$
$latex 3x+4(-5x+11)-27=0$
$latex 3x-20x+44-27=0$
$latex -17x+17=0$
Passo 4: Resolvendo para x, temos:
$latex -17x+17=0$
$latex -17x=-17$
$latex x=1$
Passo 5: Substituindo $latex x=1$ na segunda equação, temos:
$latex 5x+y-11=0$
$latex 5(1)+y-11=0$
$latex y-6=0$
$latex y=6$
A solução do sistema é $latex x=1,~~y=6$.
EXERCÍCIO 5
Encontre a solução para o sistema de equações: $latex \begin{cases}2(-x+y)=-3x+y+9 \\ 2x+y=13 \end{cases}$
Solução
Passo 1: Simplificando a primeira equação, temos:
$latex \begin{cases}x+y=9 \\ 2x+y=13 \end{cases}$
Passo 2: Resolvendo a primeira equação para y, temos:
$latex x+y=9$
$latex y=9-x$
Passo 3: Substituindo $latex y=9-x$ na segunda equação, temos:
$latex 2x+y=13$
$latex 2x+9-x=13$
Passo 4: Resolvendo para x, temos:
$latex 2x+9-x=13$
$latex x=4$
Passo 5: Substituindo $latex x=4$ na primeira equação, temos:
$latex x+y=9$
$latex 4+y=9$
$latex y=5$
A solução do sistema é $latex x=4,~~y=5$.
EXERCÍCIO 6
Encontre a solução para o sistema de equações: $latex \begin{cases}2x-3y=7 \\ 2x+3y=1 \end{cases}$
Solução
Passo 1: As equações já estão simplificadas.
Passo 2: Resolvendo a primeira equação para x, temos:
$latex 2x-3y=7$
$latex 2x=3y+7$
$latex x=\frac{3y+7}{2}$
Passo 3: Substituindo $latex x=\frac{3y+7}{2}$ na segunda equação, temos:
$latex 2x+3y=1$
$latex 2\left(\frac{3y+7}{2}\right)+3y=1$
$latex 3y+7+3y=1$
Passo 4: Resolvendo para y, temos:
$latex 3y+7+3y=1$
$latex 6y=-6$
$latex y=-1$
Passo 5: Substituindo $latex y=-1$ na segunda equação, temos:
$latex 2x+3y=1$
$latex 2x+3(-1)=1$
$latex 2x-3=1$
$latex 2x=4$
$latex x=2$
A solução do sistema é $latex x=2,~~y=-1$.
EXERCÍCIO 7
Resolva o sistema de equações usando o método de substituição: $latex \begin{cases}3x-4y=5 \\ 6x-4y=2 \end{cases}$
Solução
Passo 1: Podemos simplificar a segunda equação dividindo-a por 2:
$latex \begin{cases}3x-4y=5 \\ 3x-2y=1 \end{cases}$
Passo 2: Resolvendo a segunda equação para x, temos:
$latex 3x-2y=1$
$latex 3x=2y+1$
$latex x=\frac{2y+1}{3}$
Passo 3: Substituindo $latex x=\frac{2y+1}{3}$ na primeira equação, temos:
$latex 3x-4y=5$
$latex 3\left(\frac{2y+1}{3}\right)-4y=5$
$latex 2y+1-4y=5$
Passo 4: Resolvendo para y, temos:
$latex 2y+1-4y=5$
$latex -2y=4$
$latex y=-2$
Passo 5: Substituindo $latex y=-2$ na segunda equação, temos:
$latex 3x-2y=1$
$latex 3x-2(-2)=1$
$latex 3x+4=1$
$latex 3x=-3$
$latex x=-1$
A solução do sistema é $latex x=-1,~~y=-2$.
Sistemas de equações por substituição – Exercícios para resolver
Resolva o sistema de equações: $latex \begin{cases}x-2y=5 \\ 3x+y=8 \end{cases}$
Escreva a resposta na forma x=?, y=?.
Veja também
Interessado em aprender mais sobre sistemas de equações? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
