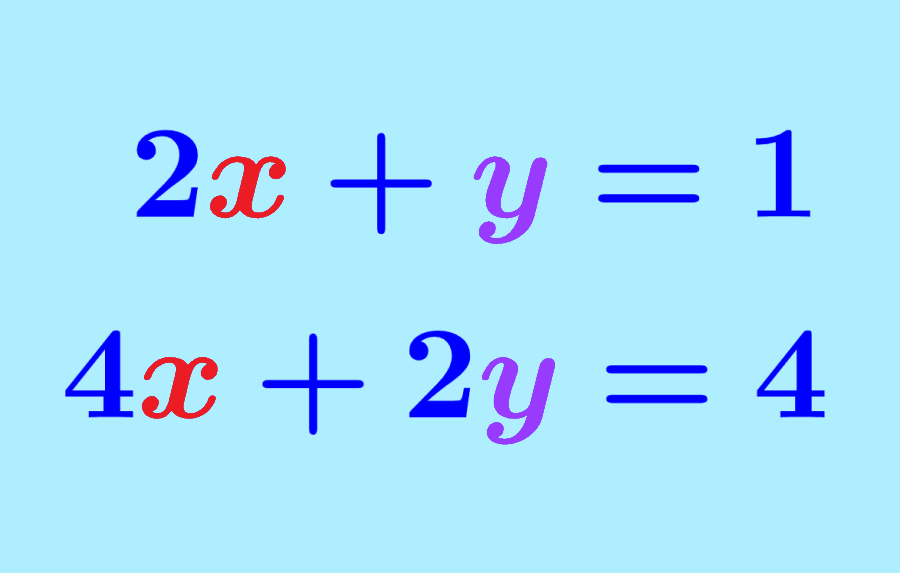Sistemas de equações sem solução, com infinitas soluções

Sistemas de equações e suas soluções

Sistemas de equações são conjuntos de duas ou mais equações que devem ser resolvidas simultaneamente. Uma solução para o sistema de equações deve satisfazer todas as equações do sistema ao mesmo tempo.

No caso de sistemas de equações 2×2, uma solução para o sistema é um par ordenado $latex (x,~y)$ que torna ambas as equações verdadeiras. Uma solução é o que as equações têm em comum, é o lugar onde suas retas se cruzam.

Se um par ordenado satisfaz apenas uma das equações do sistema, mas não a outra, então não é uma solução para o sistema de equações.

Dependendo se o sistema de equações tem soluções ou não, podemos ter dois tipos de sistemas de equações, sistemas consistentes e sistemas inconsistentes.

• Um sistema consistente é um sistema que tem pelo menos uma solução.
• Um sistema inconsistente é um sistema que não tem soluções.

Existem três resultados possíveis que podemos encontrar ao trabalhar com sistemas de equações lineares:

1. Uma solução

2. Sem solução

3. Soluções infinitas.

Sistemas de equações com apenas uma solução

Para sistemas de duas equações em duas variáveis, um par ordenado $latex (x,~y)$ é uma solução para o sistema somente se satisfizer ambas as equações. Ou seja, usando o par ordenado em cada uma das equações, ambas as equações devem ser verdadeiras.

Um sistema de equações lineares de duas ou mais equações com duas ou mais variáveis ​​terá apenas uma solução quando as equações do sistema forem diferentes umas das outras e não forem paralelas. Os detalhes desses casos são mostrados a seguir.

Quando obtemos uma solução única para o sistema de equações como resposta final, o sistema é consistente. O gráfico a seguir mostra um sistema de duas equações com duas incógnitas com uma solução:

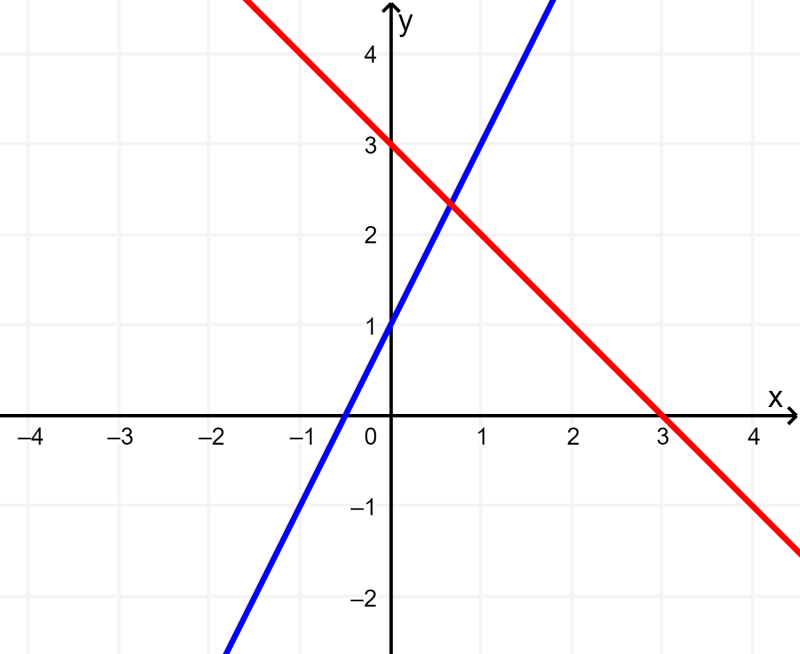
Podemos ver que os gráficos das equações do sistema se interceptam em apenas um ponto.

Assim, no caso de sistemas de equações lineares, uma maneira de determinar se o sistema terá uma solução única é desenhar gráficos simples das equações e ver se as linhas se cruzam em um único ponto.

Sistemas de equações sem solução

Sistemas de equações lineares podem não ter solução quando os gráficos de suas equações são paralelos. Se as retas nas equações forem paralelas, as retas nunca se cruzarão.

Nesses casos, as equações do sistema não têm nenhum ponto em comum, portanto, não há solução que satisfaça todas as equações do sistema. Esses tipos de sistemas de equações são inconsistentes.

No gráfico a seguir, podemos ver um sistema de duas equações com duas incógnitas que não têm solução:

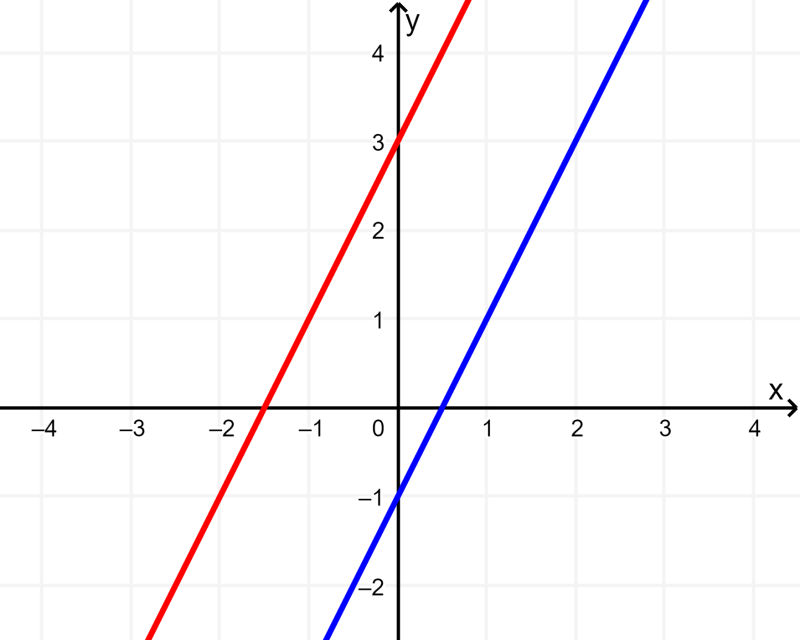
Podemos ver que os gráficos das equações são paralelos e não se cruzam, portanto não possuem pontos em comum.

Então, quando temos sistemas de equações lineares, podemos desenhar gráficos simples das equações para determinar se o sistema não tem soluções. Se pelo menos duas das retas são paralelas, o sistema não tem solução.

Algebricamente, podemos determinar se um sistema de equações lineares não tem solução comparando suas inclinações. Se as equações tiverem a mesma inclinação, as retas serão paralelas.

Sistemas de equações com soluções infinitas

Um sistema de equações lineares tem infinitas soluções quando os gráficos das equações são sobrepostos uns aos outros. Isso acontece quando temos versões equivalentes da mesma equação.

Nesse caso, teremos duas ou mais equações lineares equivalentes, portanto, qualquer solução que funcione para a primeira equação também funcionará para a segunda.

Sistemas de equações que possuem um número infinito de soluções são consistentes, pois possuem pelo menos uma solução.

No gráfico a seguir, podemos observar um sistema de duas equações com duas incógnitas que tem um número infinito de soluções:

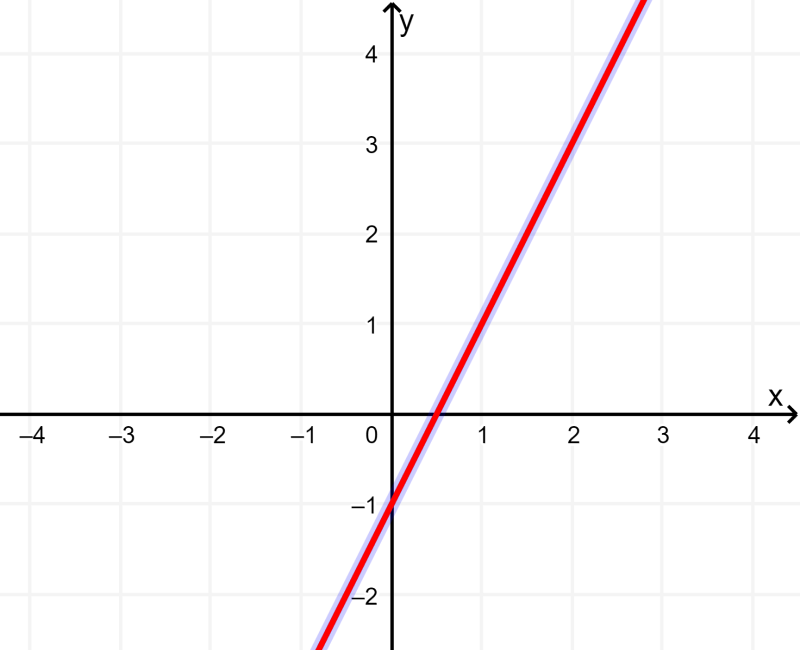
Podemos ver que as retas estão sobrepostas. Basicamente, isso significa que as equações dadas resultam na mesma reta quando representadas graficamente.

Assim, para determinar se um sistema de equações tem soluções infinitas, podemos desenhar gráficos básicos das equações e ver se as equações se sobrepõem.

Algebricamente, podemos determinar se as equações do sistema são equivalentes simplificando e manipulando-as. Por exemplo, podemos ter uma das equações igual a outra multiplicada por 2.

Veja também

Interessado em aprender mais sobre sistemas de equações? Veja estas páginas:

• Sistemas de Equações pelo Método de Eliminação
• Sistemas de Equações pelo Método da Substituição
• 10 Exercícios com Sistemas de Equações 2×2