Quando não é uma Função e Quando é?

Definições

Relações

Uma relação é um conjunto de entradas e saídas, geralmente escritos como pares ordenados (entradas, saídas). O conjunto dos primeiros componentes de cada par ordenado é denominado domínio e o conjunto dos segundos componentes de cada par ordenado é denominado imagem. Por exemplo, nos seguintes conjuntos de pares ordenados, os primeiros números em cada par são os primeiros quatro números naturais e os segundos números são o triplo do primeiro:

{(1, 3), (2, 6), (3, 9), (4, 12)}

O domínio é {1, 2, 3, 4} e a imagem é {3, 6, 9, 12}.

Cada valor no domínio também é conhecido como uma entrada ou como uma variável independente e geralmente é representado pela letra x. Cada valor na imagem também é conhecido como uma saída ou uma variável dependente e geralmente é representado pela letra y.

Funções

Uma função é um relacionamento que atribui um único valor na imagem a cada valor no domínio. Isso significa que os valores de x não se repetem. No exemplo que temos acima, relacionamos os primeiros quatro números naturais para triplicar esses números. Essa relação é de fato uma função, uma vez que cada elemento no domínio, {1, 2, 3, 4}, está emparelhado com exatamente um elemento no intervalo {3, 6, 9, 12}.

Agora, vejamos outro exemplo. Considere os seguintes pares ordenados, onde relacionamos letras a números:

{(A, 1), (B, 2), (A, 3), (B, 4)}

Observe que cada elemento no domínio {A, B} não está emparelhado com exatamente um elemento na imagem {1, 2, 3, 4}. Por exemplo, a letra A corresponde a dois valores da imagem {1, 3} e a letra B corresponde a dois valores da imagem {2, 4}. Isso significa que esse relacionamento não é uma função.

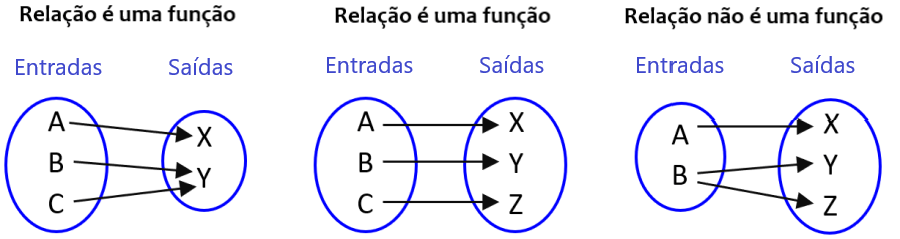
Na imagem a seguir, podemos comparar relações que são funções e não funções:

Como determinar quando é uma função e quando não é?

Para determinar se é uma função ou não, podemos usar o seguinte:

1. Identifique os valores de entrada.

2. Identifique os valores de saída.

3. Se cada valor de entrada produz apenas um valor de saída, a relação é uma função. Se cada valor de entrada produz dois ou mais valores de saída, o relacionamento não é uma função.

Também podemos resolver graficamente usando o teste de linha em diagramas de mapeamento ou o teste de linha vertical para gráficos.

Testando a linha em diagramas de mapeamento

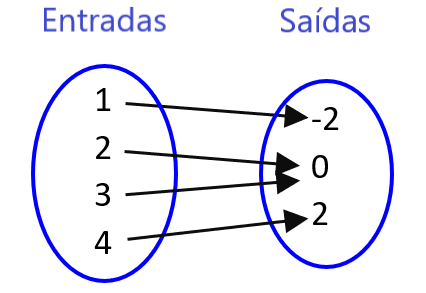
Para verificar se uma relação é uma função usando diagramas de mapeamento, usamos os seguintes critérios: se cada entrada tem apenas uma linha conectada, então as saídas representam uma função.

Por exemplo, no diagrama de mapeamento a seguir, y é uma função de x, mas x não é uma função de y.

Teste de linha vertical para gráficos

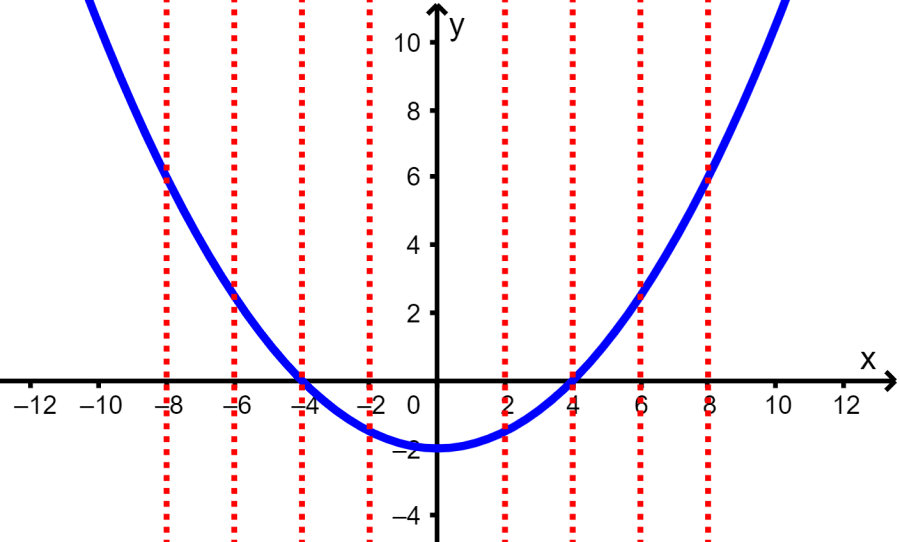
Para determinar se y é uma função de x dado um gráfico da relação, podemos usar os seguintes critérios: se todas as linhas verticais que podem ser traçadas passarem por um único ponto no gráfico, a relação é uma função. Se for possível traçar uma linha vertical que passe por pelo menos dois pontos no gráfico, então a relação não é uma função.

Por exemplo, no gráfico a seguir, podemos ver que y é uma função de x:

Exemplos com resposta

EXEMPLO 1

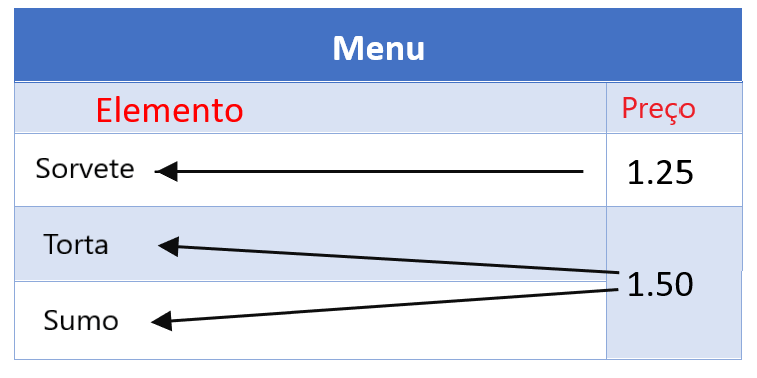
Determine se as listas de preços de um menu são funções.

Temos o menu mostrado na imagem, que consiste nos itens e seus preços.

1. O preço é uma função do item?

2. O item é função do preço?

Solução:

1. Vamos considerar os elementos como entradas. Portanto, os preços são os valores iniciais. Cada item no menu tem apenas um preço, então o preço é uma função do item.

2. Agora vamos considerar os preços como entradas. Vemos que dois itens de menu têm o mesmo preço. Isso significa que as entradas possuem mais de um valor de saída atribuído, portanto não representa uma função. Os itens não são função do preço.

EXEMPLO 2

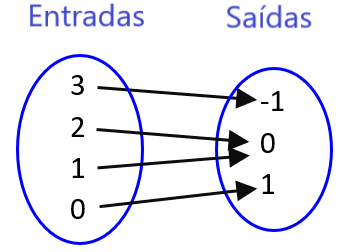
Determine se o diagrama de mapeamento a seguir representa uma função.

Solução:

Podemos ver facilmente que cada valor de entrada corresponde a um único valor de saída, portanto, o diagrama de mapeamento representa uma função.

EXEMPLO 3

Determine se o gráfico a seguir representa uma função.

Solução: podemos usar o teste da linha vertical para determinar se é uma função ou não:

Vemos que as linhas verticais desenhadas cruzam a função em um único ponto, então o gráfico representa uma função.

EXEMPLO 4

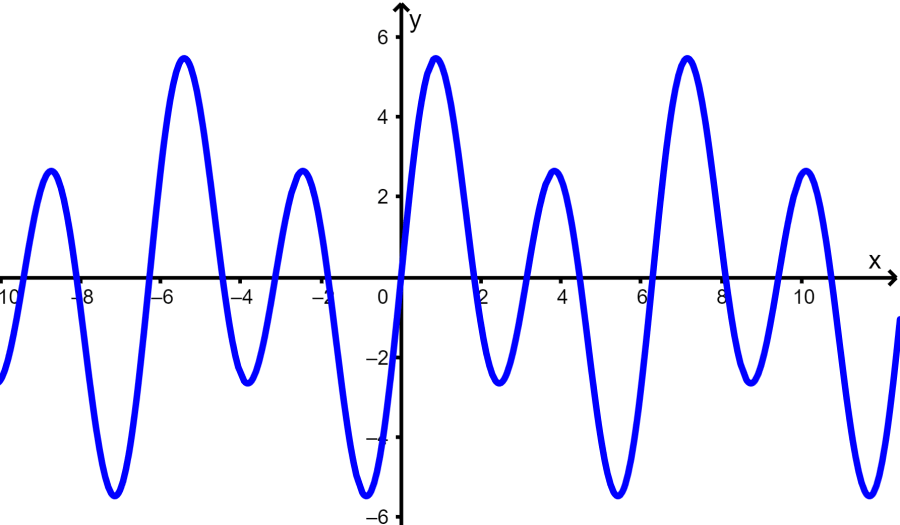
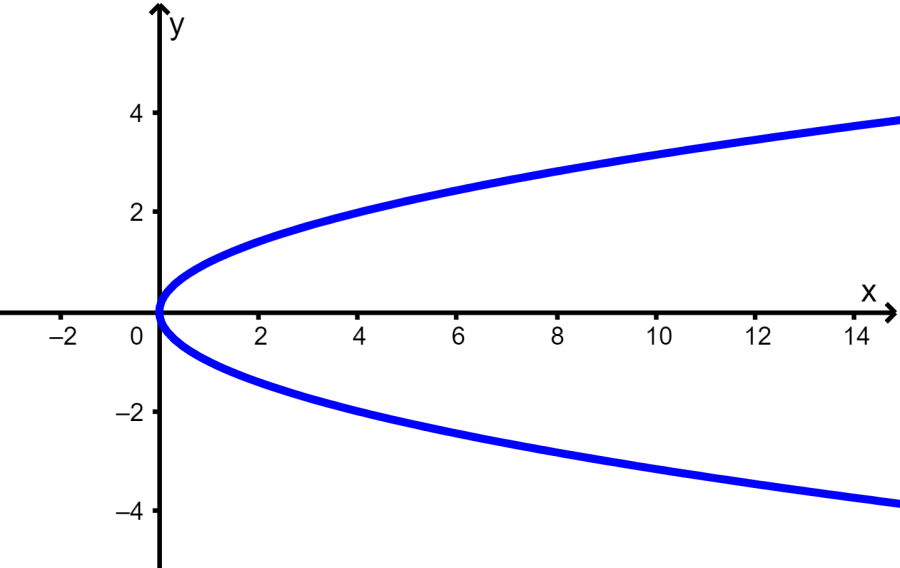
Determine se o gráfico a seguir representa uma função.

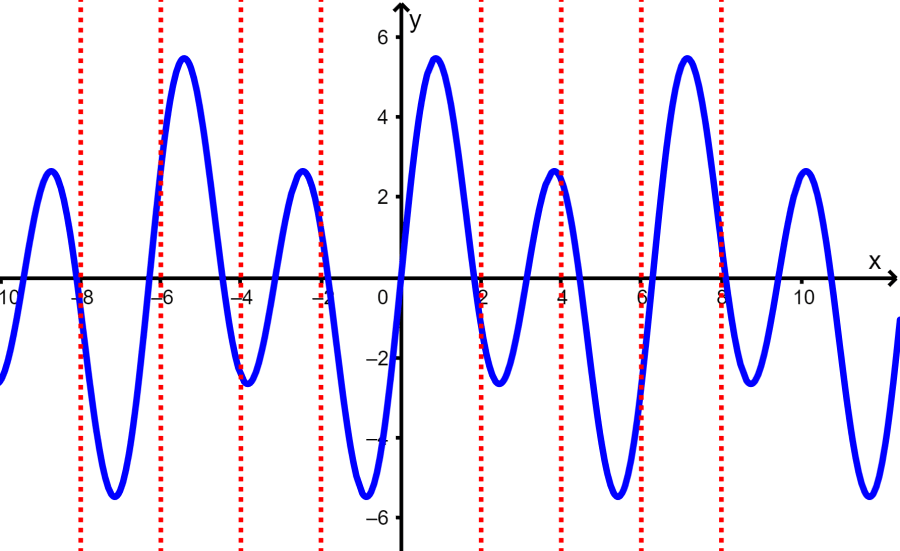
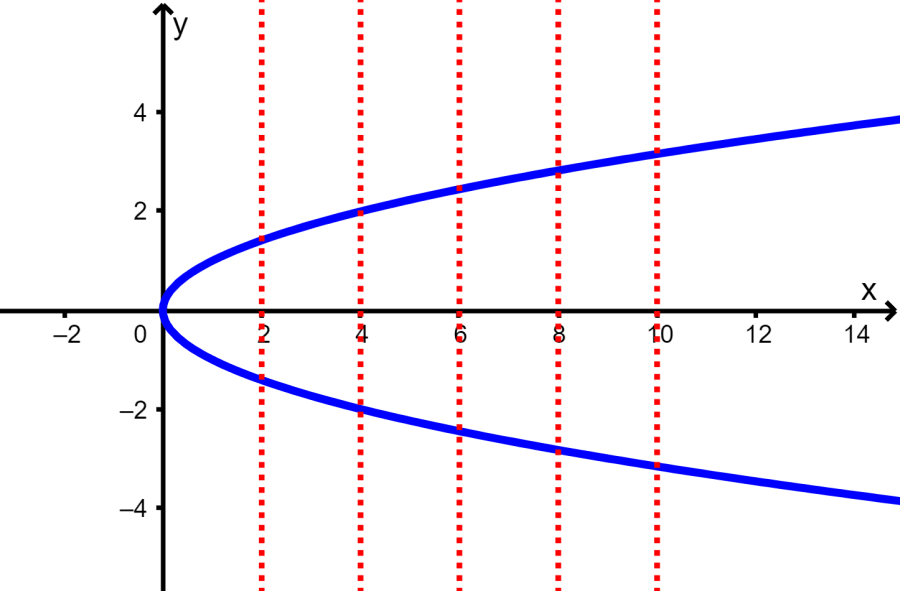
Solução: Novamente, usamos o teste da linha vertical para determinar se o gráfico é uma função ou não:

Desenhando várias linhas verticais, vemos que é possível que uma linha vertical cruze o gráfico em mais de um ponto. Isso significa que o gráfico não representa uma função.

Veja também

Você quer aprender mais sobre funções? Olha para estas páginas:

• Notação de Função Exercícios
• Parâmetros de Funções Polinomiais
• Domínio e Imagem – Definições e Exercícios