Números complexos na forma polar

Interpretação geométrica

Para entender melhor as versões alternativas dos números complexos, precisamos nos familiarizar com a interpretação geométrica desses números, pois ela nos levará diretamente à sua forma polar.

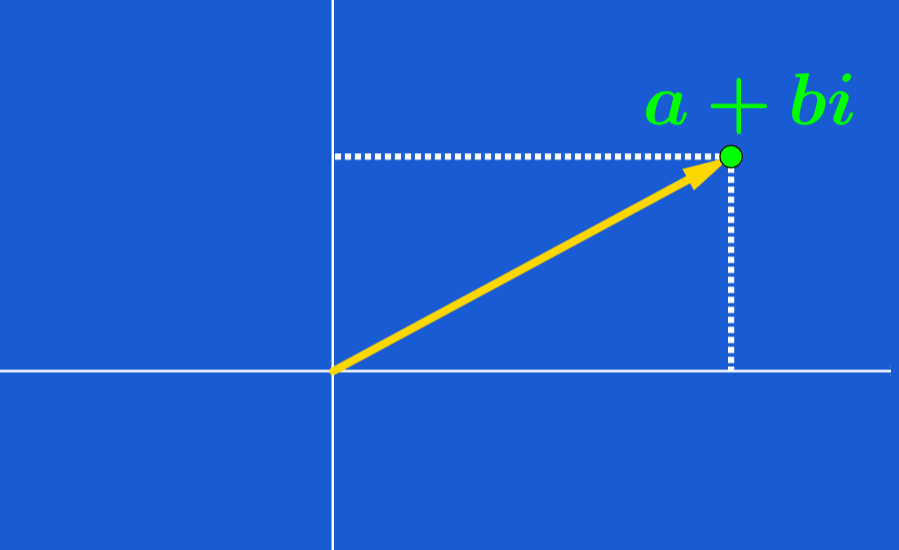
Considere o número complexo $latex z=a+bi$. Podemos pensar nesse número como o ponto $latex (a, b)$ no sistema de coordenadas cartesianas, ou como o vetor que começa na origem e termina no ponto $latex (a, b)$. O gráfico a seguir representa isso:

Nesta interpretação, o eixo x representa números reais e o eixo y representa números imaginários. Este plano é muitas vezes referido como o plano complexo.

Usando este plano, podemos obter uma interpretação geométrica do módulo ou magnitude. Podemos ver que $latex |z|=\sqrt{{{a}^2}+{{b}^2}}$ é simplesmente o comprimento do vetor usado para representar o número $latex z=a+bi $.

Forma polar

A forma polar é uma forma alternativa de escrever números complexos. Se pensarmos no número complexo $latex z=a+bi$ como o ponto $latex (a, b)$ no plano complexo, sabemos que podemos representar este ponto usando as coordenadas polares $latex (r, \theta )$, onde r é a distância do ponto à origem e θ é o ângulo, geralmente em radianos, do eixo x positivo ao vetor que liga o ponto à origem.

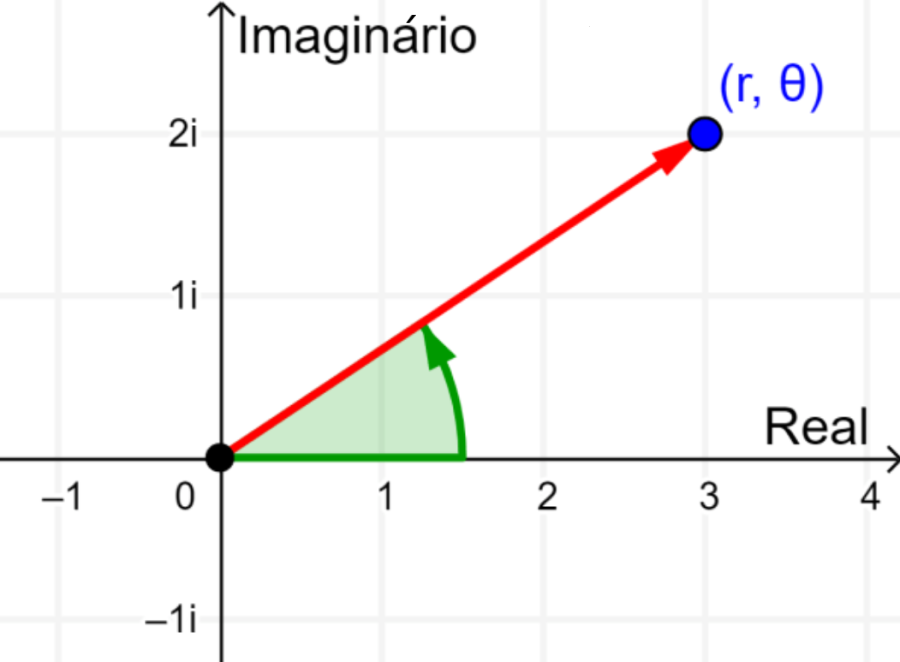
Ao trabalhar com números complexos, assumimos que r é positivo e que θ pode ser qualquer ângulo positivo ou negativo possível que termine no vetor. Consideramos apenas a forma polar dos números complexos não nulos, pois o ângulo θ não está definido para o ponto (0, 0).

Podemos converter as coordenadas polares $latex (r, \theta)$ para as coordenadas cartesianas correspondentes do ponto $latex (a, b)$ usando as seguintes fórmulas:

$latex a=r~\cos(\theta)$       $latex b=r ~\sin(\theta)$

Da mesma forma, também temos a seguinte fórmula para obter r usando as coordenadas cartesianas a e b:

$latex r=\sqrt{{{a}^2}+{{b}^2}}$

O lado direito desta fórmula é a definição da magnitude do número complexo, então temos:

$latex r=|z|$

Usando isso, podemos escrever números complexos em sua forma polar:

$latex z=r(\cos(\theta)+i~\sin(\theta)$ $latex z=|z|(\cos(\theta)+i~\sin(\theta)$

O ângulo $latex \theta $ é chamado de argumento de z e é denotado por:

$latex \theta=arg(z)$

O argumento de z pode ser qualquer um dos infinitos valores possíveis de $latex \theta$, que podem ser encontrados resolvendo:

$latex \tan(\theta)=\frac{b}{a}$

e precisamos ter certeza de que $latex \theta$ está no quadrante correto.

Suponha que temos um número complexo z com um argumento $latex \theta$. Se aumentarmos o valor de $latex \theta$, estamos girando o ponto em torno da origem no sentido anti-horário.

Como $latex 2\pi$ representa uma revolução completa, estaríamos de volta ao ponto de partida quando chegarmos a $latex \theta +2\pi$. Isso significa que $latex \theta $ e $latex \theta+2\pi$ são equivalentes.

Continuando com essa ideia, toda vez que somamos múltiplos de $latex 2\pi$, obtemos um ângulo equivalente ao ângulo original.

Operações de números complexos na forma polar

A forma polar dos números complexos pode facilitar algumas operações.

Números iguais na forma polar

Para que dois números complexos sejam iguais, seus módulos devem ser os mesmos e seus argumentos devem diferir em 2kπ, onde k é qualquer número inteiro.

Por exemplo, se temos $$r(\cos (t)+i\sin (t))=R(\cos (T)+i\sin (T))$$, então devemos ter $latex r = R$ e $latex T=t+2k\pi$.

Conjugado de um número complexo na forma polar

O número conjugado do número $latex a+bi$ é $latex a-bi$. Na forma polar, o conjugado do número polar $latex r(\cos (t)+i\sin (t))$ é $latex r(\cos (-t)+i\sin (-t))$.

Produto de números complexos na forma polar

Para multiplicar dois números complexos na forma polar, temos que multiplicar seus módulos e somar seus argumentos. Então nós temos:

$$ r(\cos (t)+i\sin (t))\times R(\cos (T)+i\sin (T))$$

$latex =rR(\cos (t+T)+i\sin (t+T))$

Divisão de números complexos na forma polar

Para dividir dois números complexos na forma polar, temos que dividir seus módulos e subtrair seus argumentos. Então nós temos:

$$\frac{r(\cos (t)+i\sin (t))}{R(\cos (T)+i\sin (T))}$$

$latex =\frac{r}{R}(\cos (t-T)+i\sin (t-T))$

Exercícios de números complexos na forma polar

Os exercícios a seguir são alguns exemplos de operações com números complexos na forma polar.

Veja também

Interessado em aprender mais sobre números complexos? Veja estas páginas:

• Magnitude de um Número Complexo com Exemplos
• Operações com Números Complexos
• Aplicações de Números Complexos