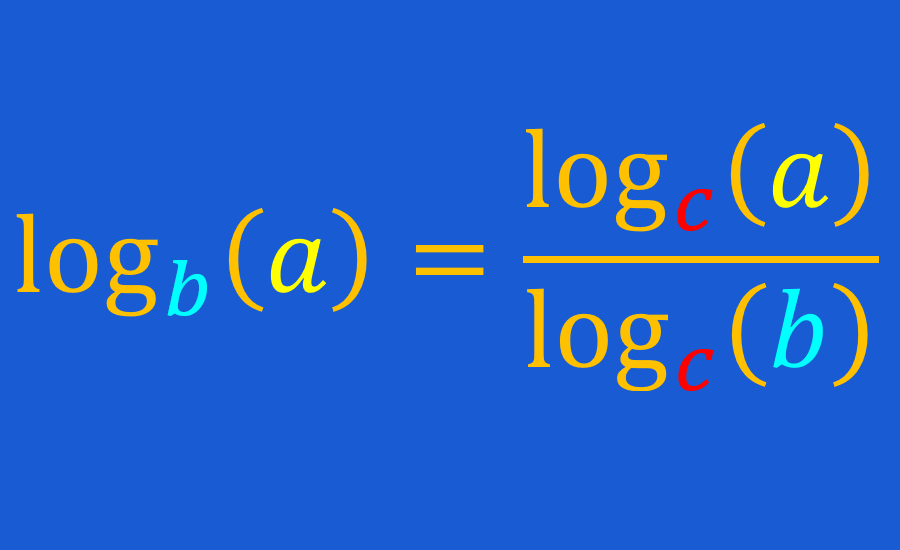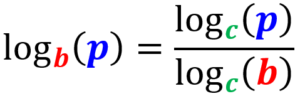A fórmula para mudança de bases de logaritmos pode ser útil quando não temos calculadoras que nos permitem inserir logaritmos de nenhuma base. Usando esta fórmula, podemos reescrever os logaritmos como uma divisão de logaritmos com a mesma base.
A seguir, conheceremos a fórmula para a mudança das bases dos logaritmos. Além disso, aprenderemos a aplicar esta fórmula usando vários exercícios resolvidos.
Fórmula de mudança de bases de logaritmos
Você deve ter notado que muitas calculadoras permitem apenas aplicar logaritmos comuns (base 10) e logaritmos naturais (base e). Podemos usar a fórmula de mudança de bases para reescrever logaritmos como o quociente de logaritmos de qualquer outra base; quando usamos uma calculadora, podemos alterá-los para logaritmos comuns ou naturais.
De acordo com a fórmula de mudança de base do logaritmo, podemos reescrever qualquer logaritmo como o quociente de dois logaritmos com uma nova base:
Teste de fórmula de mudança de base
Podemos verificar se a fórmula para a mudança de bases é verdadeira começando com o logaritmo $latex x = \log_{b}(p)$. Sabemos que logaritmos e exponenciais são funções inversas, então podemos escrever o logaritmo em sua forma exponencial:
⇒ $latex {{b}^x}=p$
Agora, podemos aplicar um logaritmo com base “c” em ambos os lados da expressão e temos:
$latex \log_{c}({{b}^{x}})=\log_{c}(p)$
Podemos usar a regra de potência para logaritmos, o que nos diz que podemos reescrever da seguinte maneira:
$latex (x)\log_{c}(b)=\log_{c}(p)$
Podemos dividir os dois lados por $latex \log_{c}(b)$ para isolarx:
$latex x=\frac{\log_{c}(p)}{\log_{c}(b)}$
Agora, substituímos o valor original de x, $latex x=\log_{b}(p)$:
| $latex \log_{b}(p)=\frac{\log_{c}(p)}{\log_{c}(b)}$ |
Em termos práticos, esta fórmula nos diz que podemos avaliar um logaritmo com uma base não padrão, convertendo-o em uma fração da forma “(logaritmo com base padrão de argumento) dividido por (logaritmo com a mesma base padrão de não base padrão) “.
Exercícios de mudança de bases de logaritmos resolvidos
Os exercícios a seguir praticam o uso da fórmula para a mudança das bases do logaritmo. Cada exercício tem sua respectiva solução, mas é recomendável que você tente resolver os exercícios antes de olhar a resposta.
EXERCÍCIO 1
Escreva $latex \log_{3}(7)$ como um quociente de logaritmos naturais.
Solução
Como vamos expressar o logaritmo como um quociente de logaritmos naturais, a nova base é e.
Reescrevemos o logaritmo como um quociente de logaritmos naturais usando a fórmula de mudança de bases. O numerador do quociente será o logaritmo natural com o argumento 7. O denominador do quociente será o logaritmo natural com o argumento 3:
$latex \log_{3}(7)=\frac{\log_{e}(7)}{\log_{e}(3)}$
$latex =\frac{\ln(7)}{\ln(3)}$
EXERCÍCIO 2
Avalie $latex \log_{2}(10)$ usando a fórmula de mudança de bases com uma calculadora.
Solução
De acordo com a fórmula para mudança de bases, podemos escrever o logaritmo da base 2 como um logaritmo de qualquer outra base. Como as calculadoras contêm o log natural, podemos usar o logaritmo natural:
$latex \log_{2}(10)=\frac{\ln(10)}{\ln(2)}$
$latex \approx 3.3219$
EXERCÍCIO 3
Converta $latex \log_{2}(7)$ como um logaritmo com base 5.
Solução
Embora a transformação para um logaritmo com base 5 não seja muito útil para a resolução de problemas, esses exercícios têm o objetivo de praticar o uso da fórmula de mudança de bases. Então, temos:
$latex \log_{2}(7)=\frac{\log_{5}(7)}{\log_{5}(2)}$
EXERCÍCIO 4
Encontre o logaritmo $latex \log_{3} (6)$.
Solução
O argumento é 6 e a base é 3. Podemos usar a fórmula para mudança de bases e escrever como um quociente de logaritmos naturais:
$latex \log_{3}(6)=\frac{\ln(6)}{\ln(3)}$
$latex =\frac{1.7916}{1.6309}$
Se arredondarmos para três casas decimais, a resposta final é:
$latex \log_{3}(6)=1.631$
Também podemos usar o logaritmo comum:
$latex \log_{3}(6)=\frac{\log(6)}{\log(3)}$
$latex =\frac{0.7782}{0.4771}$
$latex =1.631$
Podemos ver que não importa qual base usamos na fórmula de mudança de bases. A única coisa importante é que mantenhamos a mesma base tanto no numerador quanto no denominador.
EXERCÍCIO 5
Simplifique a expressão $latex \frac{\log(625)}{\log(25)}$ para obter um único número real.
Solução
Nesse caso, podemos usar a fórmula de mudança de base reversa, ou seja, começamos com o quociente e obtemos o seguinte logaritmo:
$latex \frac{\log(625)}{\log(25)}=\log_{25}(625)$
Agora, podemos reescrever esse logaritmo como uma potência para uma resolução mais fácil. Dizemos que o resultado deste logaritmo é dado pela letra x:
$latex {{25}^x}=625$
Podemos reescrever isso como potências com a mesma base:
$latex {{({{5}^2})}^x}={{5}^4}$
$latex {{5}^{2x}}={{5}^4}$
Como as bases são equivalentes, isso significa que os expoentes também devem ser equivalentes para que a equação seja verdadeira. Então, temos :
$latex 2x=4$
$latex x=2$
Portanto, o valor da expressão original é 2.
Exercícios de mudança de bases de logaritmos para resolver
Pratique o que aprendeu sobre a fórmula de mudança de bases com os exercícios a seguir. Resolva os exercícios e selecione sua resposta. Verifique para ter certeza de que selecionou a correta.
Veja também
Você quer aprender mais sobre logaritmos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
