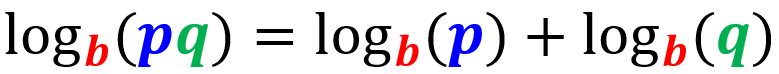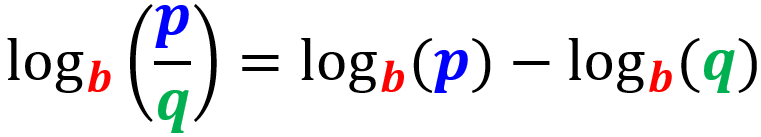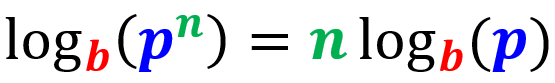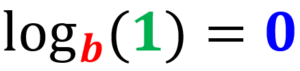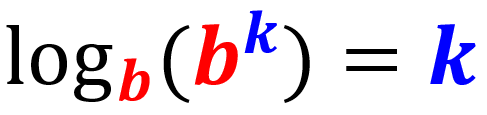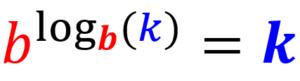Expressões logarítmicas podem ser simplificadas, expandidas e resolvidas usando as regras de logaritmos. As regras dos logaritmos nos mostram diferentes maneiras em que uma expressão logarítmica pode ser escrita.
A seguir, veremos um resumo das principais regras dos logaritmos. Além disso, veremos vários exercícios resolvidos com logaritmos para aprender como aplicar as regras dos logaritmos para resolver exercícios algébricos.
Resumo de regras dos logaritmos
O logaritmo de um número é a potência à qual o número deve ser elevado para obter um valor específico. Por exemplo, o logaritmo de base 2 de 8 é 3, já que 2 elevado à potência de 3 é igual a 8:
$latex \log_{2}(8)=3$
já que:
$latex {{2}^3}=8$
A seguir temos as regras logarítmicas mais importantes que podem nos ajudar a simplificar ou reescrever expressões logarítmicas complexas.
Regra do produto
O logaritmo de um produto pode ser escrito como a soma dos logaritmos dos fatores individuais:
Regra do quociente
O logaritmo de um quociente pode ser reescrito como o logaritmo do numerador menos o logaritmo do denominador:
Regra de potência
O logaritmo de uma expressão exponencial pode ser reescrito como o expoente multiplicado pelo logaritmo da base (sem o expoente):
Regra de zero
O logaritmo de 1, onde a base é $latex b> 0$, mas $latex b \neq 0$, é igual a zero:
Regra de identidade
O logaritmo de um número igual à base é igual a 1. Temos que o argumento é igual à base, então b deve ser maior que zero, mas não pode ser igual a 1:
Regra do logaritmo do expoente
Ao aplicar o logaritmo de um número exponencial com a mesma base do logaritmo, o resultado é o expoente:
Regra do expoente de um logaritmo
Tendo um número elevado a um logaritmo, onde a base do logaritmo é igual à base do número, o resultado é o argumento do logaritmo:
Exercícios sobre logaritmos resolvidos
Os exercícios de logaritmo a seguir são resolvidos usando as regras dos logaritmos resumidas acima. Cada exercício tem sua respectiva solução, mas é recomendável que você mesmo resolva os exercícios antes de olhar a resposta.
EXERCÍCIO 1
Resolva o seguinte: $latex \log_{4}(8)+\log_{4}(8)$.
Solução
Usando a regra do produto dos logaritmos, temos:
$latex \log_{4}(8)+\log_{4}(8)=\log_{4}(8\times 8)$
$latex =\log_{4}(64)$
Agora, podemos escrever o logaritmo em sua forma exponencial para obter o expoente:
$latex 64={{4}^3}$
Portanto, a resposta é 3.
EXERCÍCIO 2
Resolva a seguinte expressão: $latex \log_{5}(100)-\log_{5}(4)$.
Solução
Podemos aplicar a regra do quociente de logaritmos para formar uma única expressão com a subtração de logaritmos:
$latex \log_{5}(100)-\log_{5}(4)=\log_{5}(\frac{100}{4})$
$latex =\log_{5}(25)$
Reescrevendo a expressão em sua forma exponencial, podemos encontrar o expoente:
$latex 25={{5}^2}$
Portanto, a resposta é 2.
EXERCÍCIO 3
Qual é o valor de $latex \log_{\sqrt{2}}(64)$?
Solução
Começamos escrevendo 64 como um exponencial e então aplicamos a regra de potência:
$latex \log_{\sqrt{2}}(64)=\log_{\sqrt{2}}{{(2)}^6}$
$latex =6\log_{\sqrt{2}}(2)$
Podemos escrever 2 como exponencial e reutilizar a regra de potência:
$latex =6\log_{\sqrt{2}}{{(\sqrt{2})}^2}$
$latex =6\times 2\log_{\sqrt{2}}(\sqrt{2})$
$latex =6\times 2(1)$
$latex =12$
EXERCÍCIO 4
Simplifique a seguinte expressão $$\log_{3}(108)-2\log_{3}(2)+\log_{5}(12.5)+\log_{5}(10)$$
Solução
Podemos simplificar essa expressão separando-a em duas partes. Vamos simplificar os logaritmos para a base 3 e os logaritmos para a base 5 separadamente.
Então, vamos usar a regra do quociente para simplificar os logaritmos da base 3 e usaremos a regra do produto para simplificar os logaritmos da base 5.
No entanto, temos que começar aplicando a regra da potência ao logaritmo da base 3:
$$\log_{3}(108)-2\log_{3}(2)+\log_{5}(12.5)+\log_{5}(10)$$
$$=\log_{3}(108)-\log_{3}{{(2)}^2}+\log_{5}(12.5)+\log_{5}(10)$$
$$=\log_{3}(108)-\log_{3}(4)+\log_{5}(12.5)+\log_{5}(10)$$
$latex =\log_{3}(\frac{108}{4})+\log_{5}(12.5\times 10)$
$latex =\log_{3}(27)+\log_{5}(125)$
Se escrevermos os argumentos como potências, podemos aplicar a regra de potência dos logaritmos:
$latex =\log_{3}({{3}^3})+\log_{5}({{5}^3})$
$latex =3\log_{3}(3)+3\log_{5}(5)$
$latex =3(1)+3(1)$
$latex =6$
EXERCÍCIO 5
Simplifique a seguinte expressão $latex \log_{5}(500)-2\log_{5}(2)+\log_{6}(216)$.
Solução
Podemos aplicar a regra do produto aos logaritmos com base 5 e podemos aplicar a regra da potência ao logaritmo com base 6:
$latex \log_{5}(500)-2\log_{5}(2)+\log_{6}(216)$
$latex =\log_{5}(500)-\log_{5}({{2}^2})+\log_{6}(216)$
$latex =\log_{5}(500)-\log_{5}(4)+\log_{6}(216)$
$latex =\log_{5}(\frac{500}{4})+\log_{6}(216)$
$latex =\log_{5}(125)+\log_{6}(216)$
Agora, podemos reescrever os argumentos como potências e aplicar a lei de potência dos logaritmos:
$latex =\log_{5}({{5}^3})+\log_{6}({{6}^3})$
$latex =3\log_{5}(5)+3\log_{6}(1)$
$latex =3(1)+3(1)$
$latex =6$
EXERCÍCIO 6
Simplifique a expressão logarítmica: $latex 2\log_{3}(5)+\log_{3}(40)-3\log_{3}(10)$.
Solução
Começamos usando a regra de potência para reescrever logaritmos. Em seguida, usaremos a regra do produto e a regra do quociente para formar um único logaritmo, uma vez que todas as bases são as mesmas:
$latex 2\log_{3}(5)+\log_{3}(40)-3\log_{3}(10)$
$latex =\log_{3}({{5}^2})+\log_{3}(40)-\log_{3}({{10}^3})$
$latex =\log_{3}(25)+\log_{3}(40)-\log_{3}(1000)$
$latex =\log_{3}(\frac{25\times 40}{1000})$
$latex =\log_{3}(1)$
Agora, resolvemos aplicando a regra do zero:
$latex \log_{3}(1)=0$
EXERCÍCIO 7
Qual é a versão expandida da expressão: $latex \log_{3}(27{{x}^2}{{y}^5})$?
Solução
Temos um logaritmo de um produto de fatores, portanto, podemos usar a regra do produto para separar os fatores:
$$\log_{3}(27{{x}^2}{{y}^5})=\log_{3}(27)+\log_{3}({{x}^2})+\log_{3}({{y}^5})$$
Agora, podemos reescrever 27 como uma potência e aplicar a regra de potência a todos os logaritmos:
$latex =\log_{3}({{3}^3})+\log_{3}({{x}^2})+\log_{3}({{y}^5})$
$latex =3\log_{3}(3)+2\log_{3}(x)+5\log_{3}(y)$
$latex =3(1)+2\log_{3}(x)+5\log_{3}(y)$
$latex =3+2\log_{3}(x)+5\log_{3}(y)$
Exercícios sobre logaritmos para resolver
Teste seus conhecimentos sobre logaritmos e as regras dos logaritmos para resolver os exercícios a seguir. Se precisar de ajuda com esses problemas, você pode consultar as regras dos logaritmos ou os exercícios resolvidos acima.
Veja também
Você quer aprender mais sobre logaritmos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
