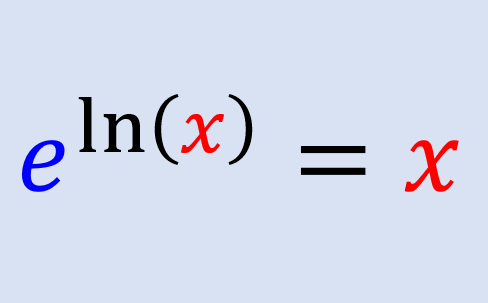Para resolver equações logarítmicas, temos que usar as regras dos logaritmos para reescrever as expressões de uma maneira mais conveniente. Depois de simplificar e reduzir as expressões logarítmicas, geralmente obteremos um dos dois tipos de equações logarítmicas. Dependendo do tipo de equação obtida, podemos obter a resposta simplesmente comparando os argumentos dos logaritmos ou podemos reescrever o logaritmo em sua forma exponencial para resolver.
A seguir, veremos um resumo das regras dos logaritmos. Além disso, veremos os dois tipos de equações logarítmicas que podemos obter. Finalmente, aprenderemos como resolver equações logarítmicas com exemplos resolvidos.
Tipos de equações logarítmicas
Geralmente, temos dois tipos de equações logarítmicas. Precisamos reconhecer esses dois casos para que seja mais fácil resolver equações logarítmicas.
- O primeiro tipo é assim:

Se tivermos apenas um logaritmo em cada lado da equação que tem a mesma base, podemos equalizar os argumentos dos logaritmos e resolver. Nesse caso, os argumentos são as expressões algébricas representadas por P e Q.
- O segundo tipo é assim:
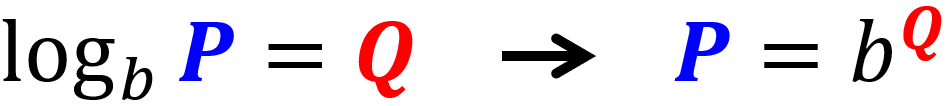
Se tivermos apenas um logaritmo em apenas um lado da equação, podemos expressá-lo como uma expressão exponencial e resolver dessa forma.
Resumo das regras dos logaritmos
Quando temos um logaritmo de um produto, podemos escrevê-lo como a soma dos logaritmos individuais dos fatores:
Regra do produto
Quando temos um logaritmo de um produto, podemos escrevê-lo como a soma dos logaritmos individuais dos fatores:
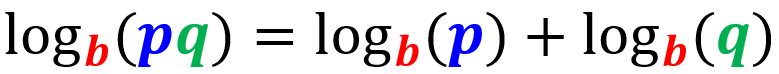
Regra do quociente
Quando temos um logaritmo de um quociente, podemos escrevê-lo como o logaritmo do numerador menos o logaritmo do denominador:
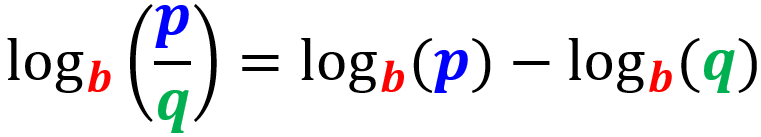
Regra de potência
O logaritmo de um valor exponencial pode ser reescrito como o expoente multiplicado pelo logaritmo da base (sem o expoente):
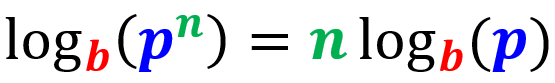
Regra de zero
O logaritmo de 1 onde a base é diferente de zero e maior que zero é igual a zero:
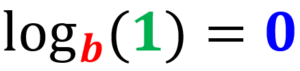
Regra de identidade
O logaritmo de um valor igual à base é igual a 1. A base, b deve ser maior que zero, mas não pode ser igual a 1:

Regra do logaritmo do expoente
O logaritmo de um valor exponencial, onde a base da potência é igual à base do logaritmo, é igual ao expoente:
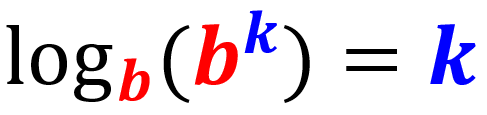
Regra do expoente de um logaritmo
Se temos um número elevado ao logaritmo com base igual ao número, isso é equivalente ao argumento do logaritmo:
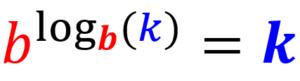
Aprender a resolver equações logarítmicas com exemplos resolvidos
EXEMPLO 1
- Resolva a equação logarítmica: $$\log_{3}(x+2)+\log_{3}(2)=\log_{3}(14)$$
Solução: Podemos usar a regra do produto para formar uma única expressão logarítmica no lado esquerdo. Então, temos:
$latex \log_{3}(x+2)+\log_{3}(2)=\log_{3}(14)$
$latex \log_{3}[(x+2)2]=\log_{3}(14)$
Usando a propriedade distributiva de multiplicação, temos:
$latex \log_{3}(2x+4)=\log_{3}(14)$
Temos um logaritmo com a mesma base em cada lado, então podemos formar uma equação com os argumentos:
$latex 2x+4=14$
Agora temos uma equação linear, então podemos resolver facilmente:
$latex 2x+4=14$
$latex 2x=10$
$latex x=5$
EXEMPLO 2
- Resolva a equação logarítmica: $$\log_{2}(x)+\log_{2}(x+2)=\log_{2}(x+12)$$
Solução: Semelhante ao exemplo anterior, podemos usar a regra do produto para formar um único logaritmo no lado esquerdo da equação:
$$\log_{2}(x)+\log_{2}(x+2)=\log_{2}(x+12)$$
$latex \log_{2}[x(x+2)]=\log_{2}(x+12)$
Usando a propriedade distributiva para distribuir o x e obter:
$latex \log_{2}({{x}^2}+2x)=\log_{2}(x+12)$
O logaritmo em ambos os lados da equação tem a mesma base, então podemos eliminá-lo e formar uma equação com os argumentos:
$latex {{x}^2}+2x=x+12$
Nesse caso, temos uma equação quadrática. Podemos mover todos os termos para um lado da equação e usar a fatoração para resolver:
$latex {{x}^2}+2x=x+12$
$latex {{x}^2}+2x-x-12=0$
$latex {{x}^2}+x-12=0$
$latex (x+4)(x-3)=0$
Tornamos cada fator igual a zero e resolvemos:
⇒ $latex x=-4$
⇒ $latex x=3$
Portanto, temos duas respostas, $latex x=-4$ e $latex x=3$.
EXEMPLO 3
- Resolva a equação logarítmica: $$\log_{2}(x+4)-\log_{2}(3)=\log_{2}(x-2)-\log_{2}(5)$$
Solução: Aqui, temos uma subtração logarítmica em cada lado da equação. Podemos usar a regra do quociente para obter um único logaritmo em cada lado:
$$\log_{2}(x+4)-\log_{2}(3)=\log_{2}(x-2)-\log_{2}(5)$$
$latex \log_{2}(\frac{x+4}{3})=\log_{2}(\frac{x-2}{5})$
Não podemos reduzir as expressões dentro de logaritmos. No entanto, como os dois logaritmos têm a mesma base, podemos eliminá-los e formar uma equação com os argumentos:
$latex \frac{x+4}{3}=\frac{x-2}{5}$
Podemos simplificar esta expressão por meio da multiplicação cruzada:
$latex 5(x+4)=3(x-2)$
Aplicamos a propriedade distributiva da multiplicação para simplificar:
$latex 5x+20=3x-6$
Temos uma equação linear, então podemos resolver facilmente:
$latex 5x+20=3x-6$
$latex 2x=-26$
$latex x=-13$
EXEMPLO 4
- Resolva a equação logarítmica: $latex \ln({{x}^2})+\frac{1}{2}\ln(4)=\ln({{x}^2}+16)$.
Solução: Aqui, temos logaritmos naturais, ou seja, logaritmos com base e. Esses logaritmos são denotados com ln. Embora sejam escritos de forma um pouco diferente, todas as regras dos logaritmos normalmente se aplicam aos logaritmos naturais..
Podemos usar a regra de potência para reescrever o logaritmo que tem uma fração na frente:
$latex \ln({{x}^2})+\frac{1}{2}\ln(4)=\ln({{x}^2}+16)$
$latex \ln({{x}^2})+\ln({{4}^{\frac{1}{2}}})=\ln({{x}^2}+16)$
$latex \ln({{x}^2})+\ln(2)=\ln({{x}^2}+16)$
Agora, podemos usar a regra do produto dos logaritmos para simplificar a parte esquerda da equação:
$latex \ln(2{{x}^2})=\ln({{x}^2}+16)$
Temos um logaritmo natural em cada lado, então podemos eliminá-lo e escrever uma equação com os argumentos:
$latex 2{{x}^2}={{x}^2}+16$
Podemos resolver essa equação quadrática facilmente:
$latex 2{{x}^2}={{x}^2}+16$
$latex 2{{x}^2}-{{x}^2}=16$
$latex {{x}^2}=16$
Tirando a raiz quadrada de ambos os lados, temos:
$latex x=\sqrt{16}$
$latex x=\pm 4$
Portanto, temos duas respostas, $latex x=4$ e $latex x=-4$.
EXEMPLO 5
- Resolva a equação logarítmica: $latex \log(5x+40)=2$.
Solução: Vemos que temos o logaritmo sem nenhuma base escrita. Quando temos isso, assumimos que o logaritmo tem base 10. Na verdade, o logaritmo com base 10 é chamado de logaritmo comum.
Nesse caso, temos apenas um logaritmo unilateral. Consideramos este como o segundo caso mencionado acima:
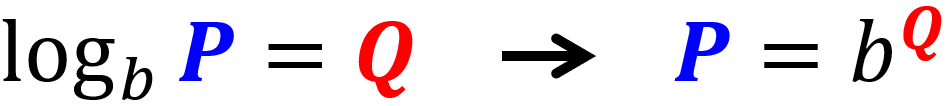
Vamos transformar a equação da forma logarítmica para a exponencial para resolver. Portanto, o argumento do logaritmo permanece no lugar e removemos o logaritmo. O número à direita se torna o expoente da base do logaritmo, que é 10:
$latex \log(5x+40)=2$
$latex 5x+40={{10}^2}$
Simplificamos o expoente e resolvemos a equação:
$latex 5x+40=100$
$latex 5x=60$
$latex x=12$
EXEMPLO 6
- Resolva a equação logarítmica: $latex \log_{2}(5x)-2=\log_{2}(2x-2)$.
Solução: Podemos mover todos os logaritmos para um lado da equação e os termos constantes para o outro lado:
$latex \log_{2}(5x)-2=\log_{2}(2x-2)$
$latex \log_{2}(5x)-\log_{2}(2x-2)=2$
Agora, podemos usar a regra do quociente para formar um único logaritmo no lado esquerdo:
$latex \log_{2}(\frac{5x}{2x-2})=2$
Agora, vamos escrever a expressão em sua forma exponencial. O argumento permanece no mesmo lugar e eliminamos o logaritmo. O 2 se torna o expoente de base:
$latex \frac{5x}{2x-2}={{2}^2}$
$latex \frac{5x}{2x-2}=4$
Podemos multiplicar en cruz para simplificar:
$latex 5x=4(2x-2)$
Simplificamos com a propriedade distributiva da multiplicação :
$latex 5x=8x-8$
Podemos facilmente resolver a equação linear:
$latex 5x-8x=-8$
$latex -3x=-8$
$latex x=\frac{8}{3}$
Veja também
Você quer aprender mais sobre logaritmos? Olha para estas páginas: