A soma de uma progressão aritmética pode ser encontrada usando duas fórmulas diferentes, dependendo da informação disponível para nós. Geralmente, a informação essencial é o valor do primeiro termo, o número de termos e o último termo ou a diferença comum.
A seguir, resolveremos vários exercícios de soma de progressões aritméticas. Além disso, veremos alguns exercícios práticos nos quais você poderá aplicar o que aprendeu.
ÁLGEBRA
Relevante para…
Resolver alguns exercícios da soma de progressões aritméticas.
ÁLGEBRA
Relevante para…
Resolver alguns exercícios da soma de progressões aritméticas.
Fórmulas para a soma de uma progressão aritmética
Progressões aritméticas são progressões em que seus termos são formados a partir do termo anterior pela adição de um certo número chamado diferença comum.
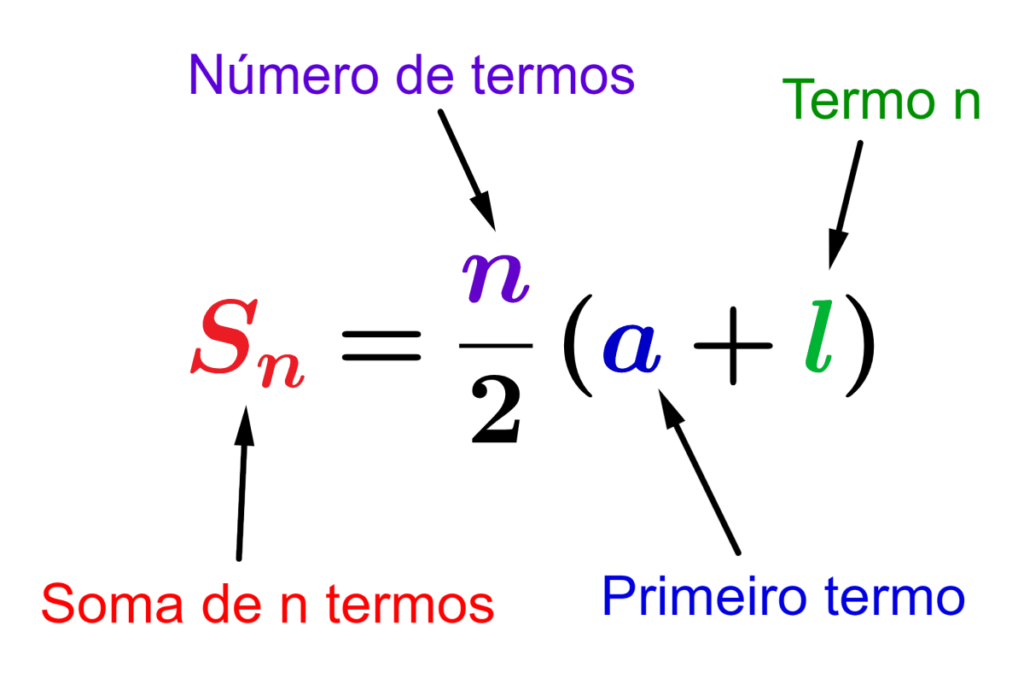
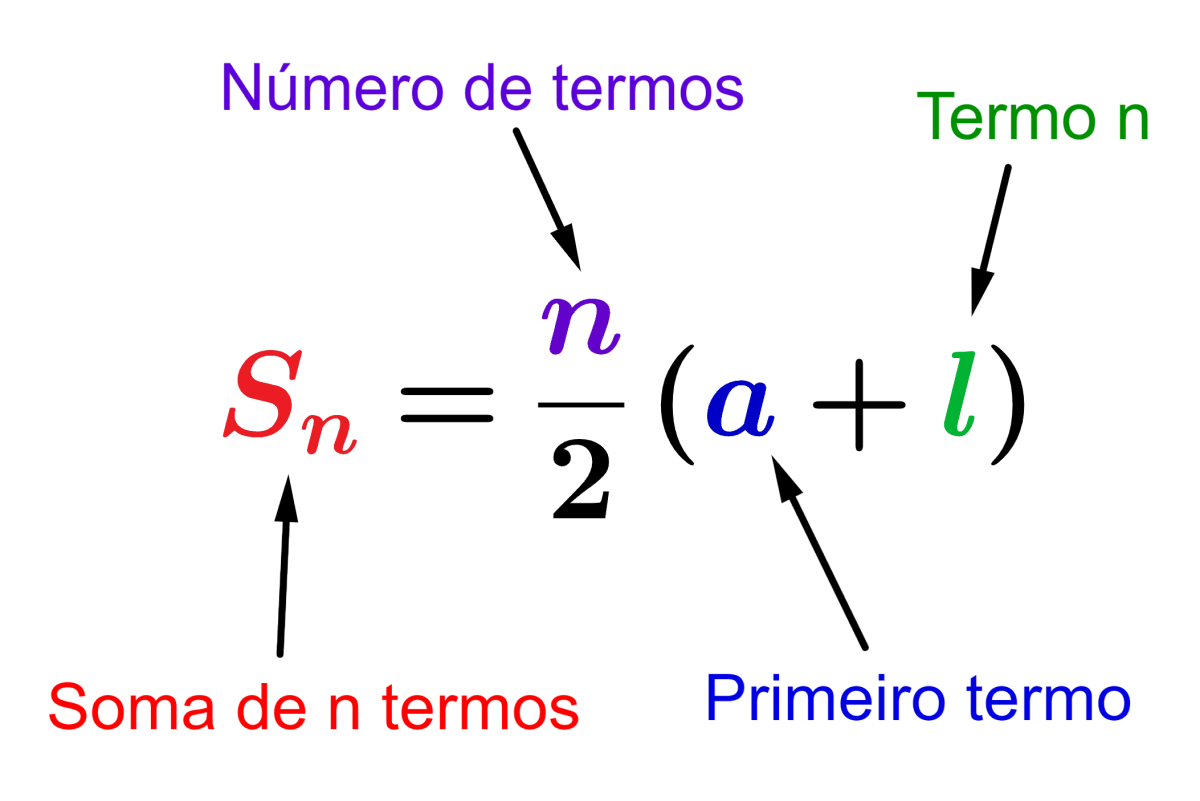
A soma dos primeiros $latex n$ termos de uma progressão aritmética pode ser encontrada com a seguinte fórmula
$$S_{n}=\frac{n}{2}(a+l)$$
onde,
- $latex a$ é o primeiro termo da progressão.
- $latex l$ é o último termo.
- $latex n $ é o número de termos.
Além disso, lembrando que qualquer termo de uma progressão aritmética pode ser encontrado usando a fórmula $latex a_{n}=a+(n-1)d$, podemos escrever a fórmula da soma da seguinte forma:
$$S_{n}=\frac{n}{2}[2a+(n-1)d]$$
onde,
- $latex a$ é o primeiro termo.
- $latex d$ é a diferença comum.
- $latex n $ é o número de termos.
Demonstração da fórmula da soma das progressões aritméticas
Lembre-se de que cada termo de uma progressão aritmética é obtido adicionando a diferença comum, d, ao termo anterior. Assim, podemos escrever o seguinte:
$$S_{n}=a+[a+d]+…+[a+(n-1)d]$$
Esta é a equação [1]. Agora, escrevemos os termos na ordem inversa, ou seja, da direita para a esquerda.
$$S_{n}=[a+(n-1)d]+[a+(n-2)d]+…+a$$
Esta é a equação [2]. Se somarmos ambas as equações, podemos obter o valor de $latex 2S_{n}$:
$$2S_{n}=(a+[a+(n-1)d])+((a+d)+[a+(n-2)d])+…+([a+(n-1)d]+a)$$
$$2S_{n}=[2a+(n-1)d]+[2a+(n-1)d]+…+[2a+(n-1)d]$$
Vemos que os termos obtidos são iguais, então a soma é igual a um dos termos multiplicado por n (número total de termos).
$$2S_{n}=n[2a+(n-1)d]$$
Finalmente, dividimos a equação inteira por 2 para encontrar $latex S_{n}$:
$$S_{n}=\frac{n}{2}[2a+(n-1)d]$$
10 Exercícios resolvidos de somas de progressões aritméticas
EXERCÍCIO 1
Encontre a soma dos 8 primeiros termos de uma progressão aritmética onde o primeiro termo é 4 e o 8º termo é 25.
Solução
Podemos começar escrevendo todos os valores que conhecemos:
- Primeiro ermo: $latex a=4$
- Último termo: $latex l=8$
- Número de termos: $latex n=8$
Agora, podemos usar a fórmula para a soma das progressões aritméticas com os valores fornecidos:
$$S_{n}=\frac{n}{2}[a+l]$$
$$S_{8}=\frac{8}{2}[4+25]$$
$$S_{8}=4[29]$$
$$S_{8}=116$$
EXERCÍCIO 2
O primeiro termo de uma progressão aritmética é 7 e o 15º termo é 63. Encontre a soma dos primeiros 15 termos.
Solução
Começamos escrevendo todos os valores conhecidos:
- Primeiro termo: $latex a=7$
- Último termo: $latex l=63$
- Número de termos: $latex n=15$
Agora, usamos a fórmula para a soma de uma progressão aritmética:
$$S_{n}=\frac{n}{2}[a+l]$$
$$S_{15}=\frac{15}{2}[7+63]$$
$$S_{15}=7,5[70]$$
$$S_{15}=525$$
EXERCÍCIO 3
Encontre a soma dos 9 primeiros termos de uma progressão aritmética onde o primeiro termo é -20 e o 9º termo é -44.
Solução
Temos as seguintes informações:
- $latex a=-20$
- $latex l=-44$
- $latex n=9$
Usando a fórmula da suma com as informações fornecidas, temos:
$$S_{n}=\frac{n}{2}[a+l]$$
$$S_{9}=\frac{9}{2}[-20-44]$$
$$S_{9}=4,5[-64]$$
$$S_{9}=-288$$
EXERCÍCIO 4
Encontre a soma dos primeiros 20 termos de uma progressão aritmética começando com 5, 9, 13, 17, …
Solução
Neste caso, não conhecemos o 20º termo da progressão. No entanto, podemos encontrar a diferença comum subtraindo um termo anterior de um termo.
Então, temos 9-5=4. E temos as seguintes informações:
- Primeiro termo : $latex a=5$
- Diferença comum: $latex d=4$
- Número de termos: $latex n=20$
Agora, usamos essa informação na segunda fórmula para a soma de uma progressão aritmética:
$$S_{n}=\frac{n}{2}[2a+(n-1)d]$$
$$S_{20}=\frac{20}{2}[2(5)+(20-1)4]$$
$$=10[10+(19)4]$$
$latex =10[10+76]$
$latex =10(86)$
$latex S_{20}=860$
EXERCÍCIO 5
Uma progressão aritmética começa com os termos 60, 55, 50, … Encontre a soma dos primeiros 12 termos.
Solução
Podemos encontrar a diferença comum subtraindo um termo de seu termo anterior: 55-60=-5. Então, temos o seguinte:
- $latex a=60$
- $latex d=-5$
- $latex n=12$
Agora, podemos usar a segunda fórmula para a soma de uma progressão aritmética com as informações fornecidas:
$$S_{n}=\frac{n}{2}[2a+(n-1)d]$$
$$S_{12}=\frac{12}{2}[2(60)+(12-1)(-5)]$$
$$=6[120+(11)(-5)]$$
$latex =6[120-55]$
$latex =6(65)$
$latex S_{12}=390$
EXERCÍCIO 6
Encontre a soma dos primeiros 25 termos de uma progressão aritmética que começa com os termos 9, -1, -11, …
Solução
A diferença comum da progressão é -1-9=-10. Assim, temos os seguintes valores:
- $latex a=9$
- $latex d=-10$
- $latex n=25$
Agora, vamos usar a segunda fórmula da soma de uma progressão aritmética:
$$S_{n}=\frac{n}{2}[2a+(n-1)d]$$
$$S_{25}=\frac{25}{2}[2(9)+(25-1)(-10)]$$
$$=12,5[18+(24)(-10)]$$
$latex =12,5[18-240]$
$latex =12,5(-222)$
$latex S_{25}=2775$
EXERCÍCIO 7
Qual é o resultado da seguinte soma da progressão aritmética?
$$6+8+10+…30$$
Solução
Podemos começar encontrando a diferença comum da progressão: 8-6=2. Então, temos:
- Primeiro termo: $latex a=6$
- Diferença comum: $latex d=2$
- Último termo: $latex l=30$
Não temos o número de termos, então podemos usar a fórmula do termo geral para encontrá-lo:
$latex a_{n}=a+(n-1)d$
$latex 30=6+(n-1)2$
$latex 24=(n-1)2$
$latex 12=n-1$
$latex n=13$
Agora que temos todas as informações necessárias, podemos usar a fórmula para a soma das progressões aritméticas:
$$S_{n}=\frac{n}{2}[a+l]$$
$$S_{13}=\frac{13}{2}[6+30]$$
$$S_{13}=\frac{13}{2}[36]$$
$$S_{13}=234$$
EXERCÍCIO 8
Encontre a soma da seguinte progressão aritmética:
$$9+13+17+…+41$$
Solução
A diferença comum é igual a 13-9=4. Assim, temos os seguintes valores:
- $latex a=9$
- $latex d=4$
- $latex l=41$
Agora, usamos a fórmula do termo geral para encontrar o valor de n:
$latex a_{n}=a+(n-1)d$
$latex 41=9+(n-1)4$
$latex 32=(n-1)4$
$latex 8=n-1$
$latex n=9$
Agora que temos todas as informações necessárias, podemos encontrar a soma da progressão:
$$S_{n}=\frac{n}{2}[a+l]$$
$$S_{9}=\frac{9}{2}[9+41]$$
$$S_{9}=\frac{9}{2}[50]$$
$$S_{9}=225$$
EXERCÍCIO 9
Qual é a soma da seguinte progressão aritmética?
$$62+60+58+…+38$$
Solução
A diferença comum da progressão é igual a 60-62=-2. Assim, temos os seguintes valores:
- $latex a=62$
- $latex d=-2$
- $latex l=38$
Agora, vamos usar a fórmula do termo geral para encontrar o valor de n:
$latex a_{n}=a+(n-1)d$
$latex 38=62+(n-1)(-2)$
$latex -24=(n-1)(-2)$
$latex 12=n-1$
$latex n=13$
Agora, encontramos a soma com esses dados:
$$S_{n}=\frac{n}{2}[a+l]$$
$$S_{13}=\frac{13}{2}[62+38]$$
$$S_{13}=\frac{13}{2}[100]$$
$$S_{13}=650$$
EXERCÍCIO 10
Se o primeiro termo de uma progressão aritmética for 2 e o n-ésimo termo for 32, encontre o valor de n se a soma dos n primeiros termos for 357.
Solução
Podemos usar a fórmula do termo geral com $latex a_{n}=32$:
$latex a+(n-1)d=32$
Além disso, como sabemos que o primeiro termo é 2, temos:
$latex 2+(n-1)d=32$
$latex (n-1)d=30~~[1]$
Agora, usamos a fórmula da soma com o valor $latex S_{n}=357$:
$$ \frac{n}{2}[2a+(n-1)d]=357$$
Como sabemos que $latex a=2$, temos:
$$ \frac{n}{2}[2(2)+(n-1)d]=357$$
$$ \frac{n}{2}[4+(n-1)d]=357~~[2]$$
Substituindo a equação [1] na equação [2], temos:
$latex n(4+30)=714$
$latex 34n=714$
$latex n=21$
Exercícios de soma de progressões aritméticas para resolver
Qual é o resultado da seguinte soma de uma progressão aritmética? $$1,3+1,6+1,9+…+4,6$$
Escreva a resposta na caixa.
Veja também
Interessado em aprender mais sobre progressões? Você pode olhar para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
