A função exponencial é uma das funções mais importantes da matemática. Para formar uma função exponencial, tornamos a variável independente o expoente. Essas funções são usadas em muitas situações da vida real. Elas são usadas principalmente para o crescimento populacional, juros compostos ou radioatividade.
A seguir, veremos um resumo das funções exponenciais. Além disso, exploraremos vários exercícios de funções exponenciais resolvidos para entender o uso dessas funções.
Resumo de funções exponenciais
Uma função exponencial é uma função matemática que tem a forma geral $latex f(x)={{b}^x}$, onde x é uma variável e b é uma constante chamada de base da função e deve ser maior que 0. No funções exponenciais, a variável de entrada, x, ocorre como um expoente.
A seguir estão as propriedades da função exponencial padrão $latex f(x)={{b}^x}$:
1. O gráfico de $latex f(x)$ sempre conterá o ponto (0, 1). Isso é equivalente a ter $latex f(0)=1$, independentemente do valor de b.
2. Para qualquer valor possível de b, temos $latex {{b}^x}>0$. Isso implica que $latex {{b}^x}$ é diferente de zero.
3. Se tivermos 0 1, o gráfico de $latex f(x)={{b}^x}$ crescerá da esquerda para a direita.
5. Se tivermos $latex {{b}^x}={{b}^y}$, isso significa que $latex x=y$.
Exercícios de funções exponenciais resolvidos
Os exercícios a seguir usam algumas das aplicações de funções exponenciais. Cada um dos exercícios tem a sua respectiva solução que pode ser útil para a compreensão do processo e raciocínio utilizado.
EXERCÍCIO 1
Dada a função $latex f(x)={{2}^x}$, encontre $latex f(-2)$.
Solução
Para avaliar qualquer função, simplesmente temos que usar a entrada fornecida. Então, temos:
$latex f(-2)={{2}^{-2}}$
$latex =\frac{1}{{{2}^2}}$
$latex =\frac{1}{4}$
EXERCÍCIO 2
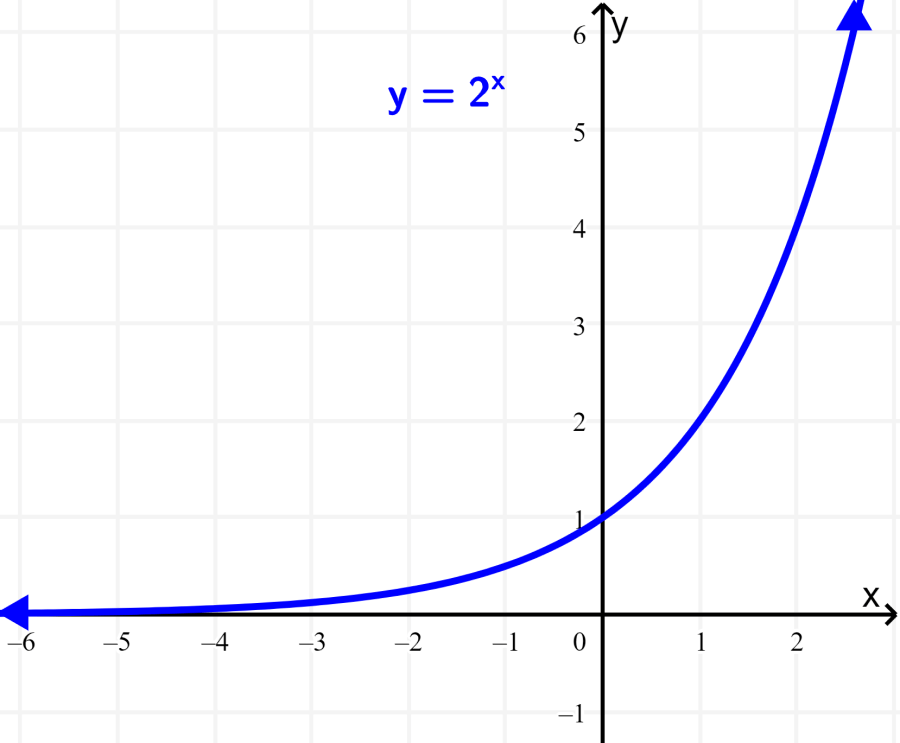
Represente graficamente a função $latex f(x)={{2}^x}$.
Solução
Para representar graficamente uma função, podemos usar vários valores x para encontrar pontos que se encontram no gráfico. Sabemos que todas as funções exponenciais passam pelo ponto (0, 1), então já temos um ponto. Além disso, podemos usar os valores $latex x=-1$, $latex x=-2$, $latex x=1$ e $latex x=2$:
- Quando $latex x=-1$, temos $latex f(-1)={{2}^{-1}}=\frac{1}{2}$.
- Quando $latex x=-2$, temos $latex f(-2)={{2}^{-2}}=\frac{1}{4}$.
- Quando $latex x=1$, temos $latex f(1)={{2}^1}}=2$.
- Quando $latex x=2$, temos $latex f(2)={{2}^2}}=4$.
Traçando esses pontos e traçando a curva, temos o seguinte:
EXERCÍCIO 3
A população de uma determinada região pode ser modelada com a fórmula $latex A=10000({{e}^{0,005t}})$, onde A representa a população e t representa o tempo em anos. Encontre a população ao final de 10 anos.
Solução
Este é um exemplo do uso de funções exponenciais para modelar o crescimento populacional. Temos a função $latex A=10000({{e}^{0.005t}})$ e temos o tempo $latex t=10$. Substituindo $latex t=10$, temos:
$latex A=10000({{e}^{0.005(10)}})$
$latex =10000({{e}^{0.05}})$
$latex =10000(1.0513)$
$latex =10513$
Então a população da região após 10 anos será 10513.
EXERCÍCIO 4
Em 1950, a população de uma cidade era de 10 000. Vinte anos depois, descobriu-se que a população era de 20 000. Encontre a função exponencial que modela a população P após t anos.
Solução
Sabemos que a função exponencial que modela o crescimento populacional tem a forma geral $latex P=N({{e}^{\lambda t}})$, onde N é a população inicial, λ é uma constante e t é o tempo. Temos que encontrar a constante λ com as informações fornecidas. Então, temos:
$latex P=N({{e}^{\lambda t}})$
$latex 20000=10000({{e}^{20 \lambda}})$
$latex \frac{20000}{10000}={{e}^{20 \lambda}}$
$latex 2={{e}^{20 \lambda}}$
$latex \ln(2)=20 \lambda$
$latex \frac{\ln(2)}{20}=\lambda$
$latex 0.0347=\lambda$
A fórmula que modela este crescimento populacional é $latex P=10000({{e}^{0.0347 t}})$.
EXERCÍCIO 5
Tomando a fórmula de crescimento populacional $latex P=N({{e}^{0,1234t}})$, estime quando a população atingirá 37 500 se em 1950 a população era de 12 500.
Solução
Com as informações fornecidas, podemos completar a fórmula de crescimento populacional:
$latex P=N({{e}^{0.1234t}})$
$latex 37500=12500({{e}^{0.1234t}})$
Agora, vamos resolver para o tempo:
$latex 37500=12500({{e}^{0.1234t}})$
$latex \frac{37500}{12500}=({{e}^{0.1234t}})$
$latex 3=({{e}^{0.1234t}})$
$latex \ln(3)=0.1234t$
$latex \frac{\ln(3)}{0.1234}=t$
$latex 8.9=t$
Isso significa que a população vai chegar 37500 em 1959.
EXERCÍCIO 6
Uma quantia de USD 10 000 é depositada em uma conta que paga juros de 7,5% compostos quatro vezes ao ano. Quanto dinheiro haverá na conta após 10 anos?
Solução
A função exponencial usada para calcular dinheiro com juros compostos é $latex D=A{{(1+ \frac{r}{n})}^{nt}}$, onde, D é o quantia final de dinheiro, A é a quantia inicial de dinheiro, r é a taxa de juros em decimais, n é o número de vezes que os juros é composto por ano e t é o tempo em anos.
Usando os dados fornecidos, temos:
$latex D=10000{{(1+\frac{0.075}{4})}^{4(10)}}$
$latex D=10000{{(1.01875)}^{40}}$
$latex D=21023.5$
Portanto, após 10 anos, haverá USD 21023,5 na conta.
EXERCÍCIO 7
Se tivermos USD 2 000 em uma conta que paga juros compostos de 7% quatro vezes ao ano, quanto tempo levará para que a conta tenha USD 10 000?
Solução
Podemos usar os dados fornecidos para formar a função exponencial de juros compostos:
$latex D=A{{(1+\frac{r}{n})}^{nt}}$
$latex 10000=2000{{(1+\frac{0.07}{4})}^{4t}}$
$latex 10000=2000{{(1.0175)}^{4t}}$
$latex \frac{10000}{2000}={{(1.0175)}^{4t}}$
$latex 5={{(1.0175)}^{4t}}$
$latex \ln(5)=\ln({{(1.0175)}^{4t}})$
$latex \ln(5)=4t\ln(1.0175)$
$latex \frac{\ln(5)}{\ln(1.0175)}=4t$
$latex \frac{99.77}{4}=t$
$latex 23.2=t$
Portanto, após 23,2 anos, haverá USD 10.000 na conta.
Exercícios de funções exponenciais para resolver
Teste seu conhecimento sobre funções exponenciais com os exercícios a seguir. Resolva os exercícios e selecione sua resposta. Verifique a resposta escolhida para ver se está correta. Veja os exercícios resolvidos acima se precisar de ajuda.
Veja também
Você quer aprender mais sobre funções? Olha para estas páginas: