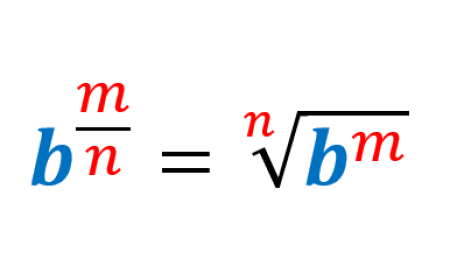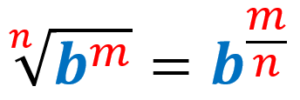Exercícios de Expoentes Fracionários Resolvidos e para Resolver

A regra do expoente fracionário nos diz que $latex {{b}^{\frac{m}{n}}}=\sqrt[n]{{{b}^m}}$. Então, escrevemos 3 elevado a 3 e então tiramos a raiz quadrada deste:

$latex 3^{\frac{3}{2}}=\sqrt[2]{3^3}$

Agora, simplificamos a expressão aplicando o expoente de 3:

$latex \sqrt[2]{3^3}=\sqrt[2]{27}$

Podemos simplificar:

$latex \sqrt[2]{27}=\sqrt[2]{9 \times 3}$

$latex =3\sqrt{3}$

Agora, temos que escrever 4 elevado à potência de 2 e tirar a raiz cúbica dessa expressão:

$latex 4^{\frac{2}{3}}=\sqrt[3]{4^2}$

Simplificamos aplicando o expoente:

$latex \sqrt[3]{4^2}=\sqrt[3]{16}$

Podemos simplificar reescrevendo 16 como 8×2:

$latex \sqrt[3]{16}=\sqrt[3]{8\times 2}$

A raiz cúbica de 8 é 2, então temos:

$latex \sqrt[3]{8\times 2}=2\sqrt[3]{2}$

Aqui temos um número e uma variável. Elevamos -2 à quarta potência e obtemos sua raiz cúbica
e elevamos x ao quadrado e obtemos sua raiz cúbica:

$latex -2^{\frac{4}{3}}x^{\frac{2}{3}}=\sqrt[3]{(-2)^4}\sqrt[3]{x^2}$

Podemos aplicar o expoente a -2 para simplificar:

$latex \sqrt[3]{(-2)^4}\sqrt[3]{x^2}=\sqrt[3]{16}\sqrt[3]{x^2}$

Semelhante ao problema anterior, podemos simplificar reescrevendo 16 como 8×2:

$latex \sqrt[3]{16}=\sqrt[3]{8\times 2}$

$latex =2\sqrt[3]{2}$

Então, temos:

$latex \sqrt[3]{16}\sqrt[3]{x^2}=2\sqrt[3]{2}\sqrt[3]{x^2}$

Agora, podemos combinar as raízes cúbicas para simplificar:

$latex 2\sqrt[3]{2}\sqrt[3]{x^2}=2\sqrt[3]{2x^2}$

Escrevemos 6 ao cubo e obtemos sua raiz quadrada. Escrevemos a x elevado à quinta e obtemos sua raiz quadrada:

$latex 6^{\frac{3}{2}}x^{\frac{5}{2}}=\sqrt{6^3}\sqrt{x^5}$

Simplificamos o 6:

$latex \sqrt{6^3}\sqrt{x^5}=\sqrt{216}\sqrt{x^5}$

É possível simplificar escrevendo 216 como 36×6:

$latex \sqrt{216}=\sqrt{36\times 6}$

$latex =6\sqrt{6}$

Então, temos:

$latex \sqrt{216}\sqrt{x^5}=6\sqrt{6}\sqrt{x^5}$

Combinando as raízes quadradas, temos:

$latex 6\sqrt{6}\sqrt{x^5}=6\sqrt{6x^5}$

Nesse caso, temos um expoente negativo. Lembre-se de que um expoente negativo pode ser transformado em positivo tomando o recíproco da base. Então, temos:

$latex {{4}^{-\frac{3}{2}}}{{x}^{\frac{1}{2}}}=\frac{{{x}^{\frac{1}{2}}}}{{{4}^{\frac{3}{2}}}}$

Agora, colocamos 4 ao cubo e obtemos sua raiz quadrada e obtemos a raiz quadrada de x:

$latex \frac{{{x}^{\frac{1}{2}}}}{{{4}^{\frac{3}{2}}}}=\frac{\sqrt{x}}{\sqrt{{{4}^3}}}$

Podemos aplicar o expoente a 4 para simplificar:

$latex \frac{\sqrt{x}}{\sqrt{{{4}^3}}}=\frac{\sqrt{x}}{\sqrt{64}}$

Agora, podemos obter a raiz quadrada de 64:

$latex \frac{\sqrt{x}}{\sqrt{64}}=\frac{\sqrt{x}}{8}$

Começamos a transformar o expoente em positivo tomando o recíproco da base. Então, temos:

$latex {{12}^{-\frac{2}{3}}}{{x}^{\frac{3}{5}}}=\frac{{{x}^{\frac{3}{5}}}}{{{12}^{\frac{2}{3}}}}$

Agora, elevamos 12 ao quadrado e obtemos sua raiz cúbica. Elevamos x ao cubo e obtemos sua quinta raiz:

$latex \frac{{{x}^{\frac{3}{5}}}}{{{12}^{\frac{2}{3}}}}=\frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{{{12}^2}}}$

Aplicamos o expoente a 12:

$latex \frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{{{12}^2}}}=\frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{144}}$

Podemos escrever 144 como 8×18 e obter a raiz cúbica de 8:

$latex \frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{144}}=\frac{\sqrt[5]{{{x}^3}}}{\sqrt[3]{8\times 18}}$

$latex =\frac{\sqrt[5]{{{x}^3}}}{2\sqrt[3]{18}}$

Simplesmente aplicamos a regra dos expoentes fracionários para formar radicais:

$latex {{x}^{{\frac{1}{2}}}}{{y}^{{\frac{2}{3}}}}=\sqrt{x}~\sqrt[3]{{{{y}^{2}}}}$

Novamente, apenas temos que aplicar a regra dos expoentes fracionários para formar radicais e então simplificar:

$latex {{81}^{{\frac{1}{4}}}}{{x}^{{\frac{3}{2}}}}=\sqrt[4]{{81}}~\sqrt{{{{x}^{3}}}}$

$latex =3~\sqrt{{{{x}^{3}}}}$

Temos expoentes negativos aqui, então começamos transformando expoentes negativos em positivos usando a regra dos expoentes negativos:

$latex {{4}^{{-\frac{1}{2}}}}{{x}^{{-\frac{1}{2}}}}=\frac{1}{{{{4}^{{\frac{1}{2}}}}{{x}^{{\frac{1}{2}}}}}}$

Agora, usamos a regra do expoente fracionário e simplificamos:

$latex =\frac{1}{{\sqrt{4}~\sqrt{x}}}$

$latex =\frac{1}{{2~\sqrt{x}}}$

Temos expoentes negativos, então começamos com a regra dos expoentes negativos:

$$\frac{{{{{16}}^{{-\frac{1}{2}}}}~{{y}^{{-\frac{1}{3}}}}}}{{{{x}^{{-\frac{1}{2}}}}~}}=\frac{{{{x}^{{\frac{1}{2}}}}~}}{{{{{16}}^{{\frac{1}{2}}}}~{{y}^{{\frac{1}{3}}}}~}}$$

Agora, usamos a regra do expoente fracionário e simplificamos:

$latex =\frac{{\sqrt{x}}}{{\sqrt{{16}}~\sqrt[3]{y}}}$

$latex =\frac{{\sqrt{x}}}{{4~\sqrt[3]{y}}}$