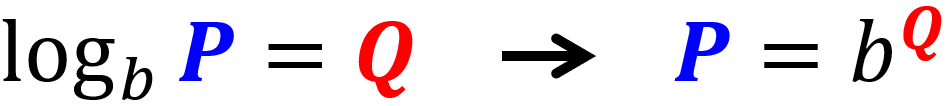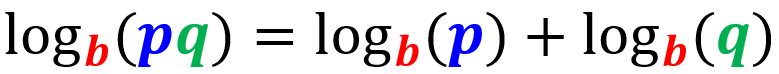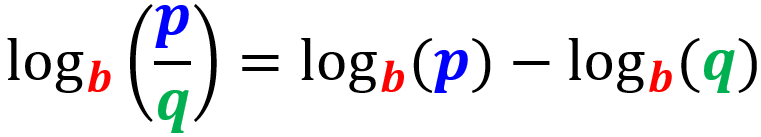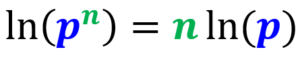Exercícios de Equações Logarítmicas Resolvidos e para Resolver

Vemos que temos uma soma de logaritmos com a mesma base no lado direito, então podemos usar a regra do produto para combiná-los. Esta é a regra do produto, caso você não se lembre dela:

Então, temos:

$latex \log_{5}(x+1)+\log_{5}(3)=\log_{5}(15)$

$latex \log_{5}[(x+1)3]=\log_{5}(15)$

Podemos expandir a multiplicação para obter:

$latex \log_{5}(3x+3)=\log_{5}(15)$

Os logaritmos têm a mesma base, então podemos eliminá-los e formar uma equação com os argumentos:

$latex 3x+3=15$

A equação linear pode ser facilmente resolvida:

$latex 3x+3=15$

$latex 3x=12$

$latex x=4$

Nesse caso, temos uma soma dos logaritmos em cada lado da equação. Então, vamos usar a regra do produto em ambos os lados para obter:

$$\log_{4}(2x+2)+\log_{4}(2)=\log_{4}(x+1)+\log_{4}(3)$$

$latex \log_{4}[(2x+2)2]=\log_{4}[(x+1)3]$

Podemos expandir a multiplicação em ambos os lados para obter:

$latex \log_{4}(4x+4)=\log_{4}(3x+3)$

Agora, eliminamos os logaritmos e formamos uma equação com os argumentos:

$latex 4x+4=3x+3$

A equação linear pode ser facilmente resolvida:

$latex 4x+4=3x+3$

$latex x=-1$

Podemos usar a regra do produto do lado esquerdo:

$$\log_{7}(x)+\log_{7}(x+5)=\log_{7}(2x+10)$$

$latex \log_{7}[x(x+5)]=\log_{7}(2x+10)$

Agora, podemos distribuir a x para obter:

$latex \log_{7}({{x}^2}+5x)=\log_{7}(2x+10)$

Podemos eliminar o logaritmo em ambos os lados, pois eles têm a mesma base e podemos formar uma equação com os argumentos:

$latex {{x}^2}+5x=2x+10$

Obtivemos uma equação quadrática. Podemos resolver esta equação colocando todos os termos de um lado e fatorando a equação:

$latex {{x}^2}+5x=2x+10$

$latex {{x}^2}+5x-2x-10=0$

$latex {{x}^2}+3x-10=0$

$latex (x+5)(x-2)=0$

Resolvemos para cada fator:

⇒   $latex x=-5$

⇒   $latex x=2$

Portanto, temos duas respostas, $latex x=-5$ e $latex x=2$.

Neste caso, temos subtrações de logaritmos em ambos os lados da equação, portanto podemos aplicar a regra do quociente dos logaritmos. Caso você não se lembre, o seguinte é a regra do quociente:

Então, aplicando esta regra a ambos os lados, temos:

$$\log_{3}(x+3)-\log_{3}(2)=\log_{3}(x-1)-\log_{3}(7)$$

$latex \log_{3}(\frac{x+3}{2})=\log_{3}(\frac{x-1}{7})$

As expressões dentro dos logaritmos não podem mais ser simplificadas. No entanto, podemos eliminar os logaritmos, pois ambos têm a mesma base:

$latex \frac{x+3}{2}=\frac{x-1}{7}$

Podemos multiplicar para simplificar:

$latex 7(x+3)=2(x-1)$

Agora, multiplicamos usando la propiedad distributiva:

$latex 7x+21=2x-2$

Resolvemos a equação linear:

$latex 7x+21=2x-2$

$latex 5x=-23$

$latex x=-\frac{23}{5}$

Podemos ver que os logaritmos nesta equação não têm base. Quando temos logaritmos sem uma base, assumimos que a base é 10. Logaritmos com base 10 são chamados de logaritmos comuns.

Nesta equação, podemos começar usando a regra de potência para reescrever o logaritmo que tem uma fração na frente dele. Caso você não se lembre, o seguinte é a regra de potência:

Então, temos:

$latex \log({{x}^2})+\frac{1}{2}\log(4)=\log({{x}^2}+16)$

$latex \log({{x}^2})+\log({{4}^{\frac{1}{2}}})=\log({{x}^2}+16)$

$latex \log({{x}^2})+\log(2)=\log({{x}^2}+16)$

Simplificamos o lado esquerdo usando a regra do produto:

$latex \log(2{{x}^2})=\log({{x}^2}+16)$

Podemos eliminar o logaritmo de cada lado, pois ele tem a mesma base:

$latex 2{{x}^2}={{x}^2}+16$

Podemos resolver para x para resolver a equação quadrática:

$latex 2{{x}^2}={{x}^2}+16$

$latex 2{{x}^2}-{{x}^2}=16$

$latex {{x}^2}=16$

Agora, pegamos a raiz quadrada de ambos os lados:

$latex x=\sqrt{16}$

$latex x=\pm 4$

Portanto, temos duas respostas, $latex x=4$ e $latex x=-4$.

Aqui também não temos uma base no logaritmo, então sabemos que é um logaritmo comum e que sua base é 10.

Nesta equação, temos um logaritmo unilateral. Esta é uma equação do segundo caso mencionado acima:

Podemos resolver essa equação escrevendo-a na forma exponencial. Portanto, removemos o logaritmo do lado esquerdo e escrevemos seu argumento. No lado direito, 2 é o expoente e 10 é a base (a base do logaritmo):

$latex \log(4x+60)=2$

$latex 4x+60={{10}^2}$

Aplicamos o expoente e resolvemos a equação linear:

$latex 4x+60=100$

$latex 4x=40$

$latex x=10$

Temos que mover os logaritmos para um lado da equação e os termos constantes para o outro lado:

$latex \log_{2}(3x)-2=\log_{2}(2x-5)$

$latex \log_{2}(3x)-\log_{2}(2x-5)=2$

Agora, simplificamos a parte esquerda usando a regra do quociente:

$latex  \log_{2}(\frac{3x}{2x-5})=2$

Para resolver, temos que escrever a equação em sua forma exponencial. O argumento permanece no mesmo lugar e eliminamos o logaritmo. Elevamos 2 (a base do logaritmo) ao expoente 2:

$latex \frac{3x}{2x-5}={{2}^2}$

$latex \frac{3x}{2x-5}=4$

Simplificamos multiplicando em cruz:

$latex 3x=4(2x-5)$

Distribuímos a multiplicação:

$latex 3x=8x-20$

Resolvemos a equação linear:

$latex 3x=8x-20$

$latex -5x=-20$

$latex x=\frac{-20}{-5}$

$latex x=4$