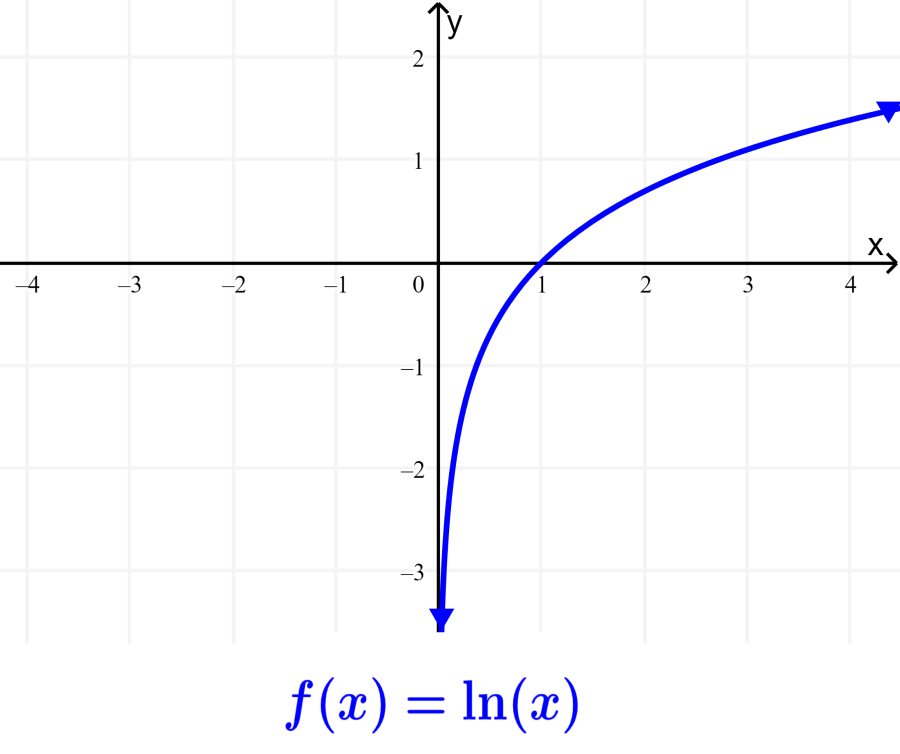
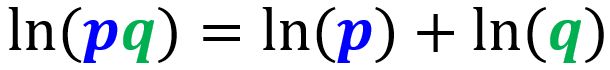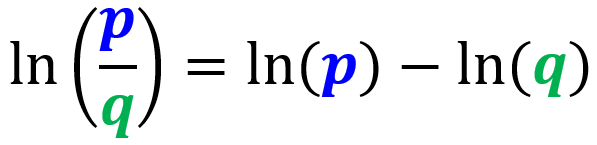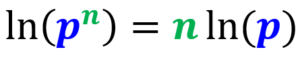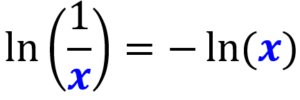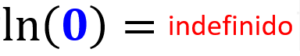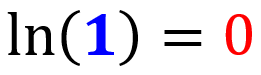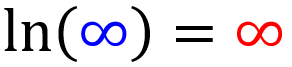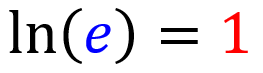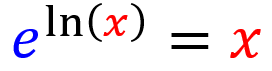As propriedades dos logaritmos naturais são importantes porque nos ajudam a simplificar e resolver problemas de logaritmos que à primeira vista parecem muito complicados. Os logaritmos naturais são denotados como ln. Esses logaritmos têm uma base de e. Lembre-se de que a letra e representa uma constante matemática conhecida como expoente natural. O valor de e é de aproximadamente 2,71828.
e aparece em muitas aplicações em matemática e até em outras áreas. Como e é tão comumente usado em matemática e economia, as pessoas que trabalham nessas áreas muitas vezes têm que aplicar o logaritmo com uma base de e de um número para resolver uma equação ou encontrar um valor, então o logaritmo natural foi criado como um atalho para escrever e calcular o logaritmo com base e.
As quatro propriedades principais dos logaritmos naturais
Propriedade do produto
A propriedade do produto dos logaritmos nos diz que podemos escrever o logaritmo de um produto como a soma dos logaritmos individuais de seus fatores:
Teste desta propriedade
Podemos começar com $latex x=\ln(p)$ e $latex y=\ln(q)$. Se escrevermos agora essas equações em sua forma exponencial, temos:
⇒ $latex {{e}^x}=p$
⇒ $latex {{e}^y}=q$
Podemos multiplicar os termos exponenciais p e q para obter:
$latex {{e}^x}\times {{e}^y}=pq$
Temos potências com a mesma base, então aplicamos a regra do produto dos expoentes para adicionar os expoentes e combinar a base:
$latex {{e}^{x+y}}=pq$
Se agora tomarmos o logaritmo natural para ambos os lados, temos:
$latex \ln({{e}^{x+y}})=\ln(pq)$
Aplicando a propriedade do poder dos logaritmos (que veremos mais tarde), temos:
$latex (x+y)\ln(e)=\ln(pq)$
$latex (x+y)=\ln(pq)$
Podemos substituir os valores originais de x e y na equação obtida:
| $latex \ln(p)+\ln(q)=\ln(pq)$ |
Propriedade do quociente
A propriedade do quociente do logaritmo natural nos diz que se tivermos um logaritmo de um quociente, podemos reescrevê-lo como o logaritmo do numerador menos o logaritmo do denominador:
Teste desta propriedade
Começamos com as equações $latex x=\ln(p)$ e $latex y=\ln(q)$. Se os reescrevermos em sua forma exponencial, temos:
⇒ $latex {{e}^x}=p$
⇒ $latex {{e}^y}=q$
Ao dividir os termos exponenciais p e q, temos:
$latex \frac{{{e}^x}} {{{e}^y}}=\frac{p}{q}$
Podemos usar a regra do quociente dos expoentes para simplificar a expressão à esquerda:
$latex {{e}^{x-y}}=\frac{p}{q}$
Se tomarmos o logaritmo natural de ambos os lados, temos:
$latex \ln({{e}^{x-y}})=\ln(\frac{p}{q})$
Aplicando a regra da potência dos logaritmos (que veremos mais tarde), temos:
$latex (x-y)\ln(e)=\ln(\frac{p}{q})$
$latex (x-y)=\ln(\frac{p}{q})$
Substituindo os valores originais de x e y na equação obtida, temos:
| $latex \ln(p)-\ln(q)=\ln(\frac{p}{q})$ |
Propriedade de potência
A propriedade de potência dos logaritmos naturais nos diz que podemos reescrever o logaritmo de um argumento exponencial da seguinte maneira:
Teste desta propriedade
Começamos com $latex x = \ln (p)$ e o reescrevemos em sua forma exponencial:
⇒ $latex {{e}^x}=p$
Se elevarmos a potência de n para ambos os lados da equação, temos:
$latex {{({{e}^x})}^n}={{p}^n}$
⇒ $latex {{e}^{xn}}={{p}^n}$
Agora, pegamos o logaritmo natural de ambos os lados:
$latex \ln({{e}^{xn}})=\ln({{p}^n})$
$latex xn~\ln(e)=\ln({{p}^n})$
$latex xn=\ln({{p}^n})$
Substituindo o valor original de x na equação obtida, temos:
| $latex n~\ln(p)=\ln({{p}^n})$ |
Propriedade recíproca
O logaritmo natural do recíproco de x é o oposto do logaritmo natural de x:
Exemplo:
$latex \ln(\frac{1}{3})=-\ln(3)$
Outras propriedades importantes dos logaritmos naturais
Além das quatro propriedades dos logaritmos naturais detalhadas acima, existem outras propriedades importantes desses logaritmos que precisamos saber se estivermos estudando logaritmos naturais. É aconselhável memorizar essas propriedades para simplificar e resolver problemas logarítmicos facilmente.
Logaritmo natural de um número negativo
O logaritmo natural de qualquer número negativo é indefinido.
Logaritmo natural de zero
O logaritmo natural de zero, ou seja, $latex \ln(0)$ também é indefinido:
Logaritmo natural de 1
O logaritmo natural de 1 é igual a zero:
Logaritmo natural do infinito
O logaritmo natural do infinito é igual ao infinito:
Logaritmo natural de e
O logaritmo natural do número natural, e, é igual a 1:
Propriedade de logaritmo do expoente
O logaritmo do exponencial e é igual ao expoente:
Propriedade do expoente de um logaritmo
Elevar e ao logaritmo natural de um número é igual ao número:
Qual é a diferença entre logaritmos naturais e outros logaritmos?
A principal diferença entre logaritmos naturais e outros logaritmos é a base que está sendo usada. Os logaritmos normalmente usam uma base de 10 (embora possa ser outro valor, que seria especificado), enquanto os logaritmos sempre usam uma base de e. Isso significa que podemos escrever:
$latex \ln(x)=\log_{e}(x)$
Se for necessário converter entre logaritmos e logaritmos naturais, você pode usar as duas equações a seguir:
$latex \log_{10}(x)=\frac{\ln (x)}{\ln (10)}$
$latex \ln(x)=\frac{\log_{10} (x)}{\log_{10} (e)}$
Além da diferença na base (que é uma grande diferença), as regras dos logaritmos e as regras dos logaritmos naturais são as mesmas.
Veja também
Você quer aprender mais sobre logaritmos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
