O teorema de Newton é uma maneira relativamente rápida de expandir expressões binomiais que são elevadas a uma potência. Neste artigo, aprenderemos como usar o teorema de Newton e examinaremos exemplos com resposta para facilitar a compreensão. Além disso, também veremos uma fórmula para calcular um termo específico em uma expansão binomial.
O que é uma expressão binomial?
Uma expressão binomial é uma expressão algébrica que contém dois termos unidos por um sinal de adição ou subtração. Por exemplo, (2+x) ou (x-4) são exemplos de expressões binomiais.
Muitas vezes, essas expressões binomiais têm expoentes e podemos precisar expandi-los totalmente:
$latex {{(x+y)}^0}=1$
$latex {{(x+y)}^1}=x+y$
$latex {{(x+y)}^2}={{x}^2}+2xy+{{y}^2}$
$latex {{(x+y)}^3}={{x}^3}+3{{x}^2}y+3x{{y}^2}+{{y}^3}$
$${{(x+y)}^4}={{x}^4}+4{{x}^3}y+6{{x}^2}{{y}^2}+4x{{y}^3}+{{y}^4}$$
Podemos ver que à medida que o expoente fica maior, a expansão dessas expressões torna-se mais tediosa e isso não é viável para expressões com expoentes muito grandes. A seguir, aprenderemos como usar o teorema binomial para expandir expressões binomiais sem a necessidade de multiplicar cada um dos termos individualmente.
Qual é o teorema de Newton?
O teorema de Newton nos diz a expansão algébrica dos expoentes de um binomial. Ou seja, o teorema de Newton nos mostra como expandir um polinômio da forma $latex {{(a+b)}^n}$ para obter todos os seus termos. Por exemplo, se quisermos expandir a expressão $latex {{(2x+y)}^5}$, precisaríamos multiplicar o binômio $latex (2x+y)$ cinco vezes, o que levaria muito tempo. O teorema de Newton permite-nos tomar um atalho usando uma fórmula para expandir esta expressão.
Com o teorema de Newton, é possível expandir a expressão $latex {{(x+y)}^n}$ para formar uma soma de termos na forma a $latex {{x}^b}{{y}^c}$, onde os expoentes b e c são não negativos e somam $latex b+c=n$. Por exemplo, considere a seguinte expressão:
$$ {{(x+y)}^4}={{x}^4}+4{{x}^3}y+6{{x}^2}{{y}^2}+4x{{y}^3}+{{y}^4}$$
O coeficiente a em qualquer termo $latex a{{x}^b}{{y}^c}$ da versão expandida é conhecido como coeficiente binomial. O coeficiente binomial também é usado em cominatórios, onde podemos obter o número de combinações diferentes de elementos b que podem ser escolhidos a partir de um conjunto de elementos n. Isso também pode ser escrito como $latex \left( {\begin{array}{*{20}{c}} n \\ b \end{array}} \right)$.
Com o teorema de Newton, podemos expandir qualquer poder de $latex (x+y)$ com uma soma da seguinte forma:
$${{\left( {x+y} \right)}^{n}}=\left( {\begin{array}{*{20}{c}} n \\ 0 \end{array}} \right){{x}^{n}}{{y}^{0}}+\left( {\begin{array}{*{20}{c}} n \\ 1 \end{array}} \right){{x}^{{n-1}}}{{y}^{1}}\left( {\begin{array}{*{20}{c}} n \\ 2 \end{array}} \right){{x}^{{n-2}}}{{y}^{2}}+\ldots +\left( {\begin{array}{*{20}{c}} n \\ {n-1} \end{array}} \right){{x}^{1}}{{y}^{{n-1}}}+\left( {\begin{array}{*{20}{c}} n \\ n \end{array}} \right){{x}^{0}}{{y}^{n}}$$
Onde cada valor $latex \left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right)$ é um número inteiro positivo conhecido como coeficiente binomial.
Teorema de Newton com triângulo de Pascal
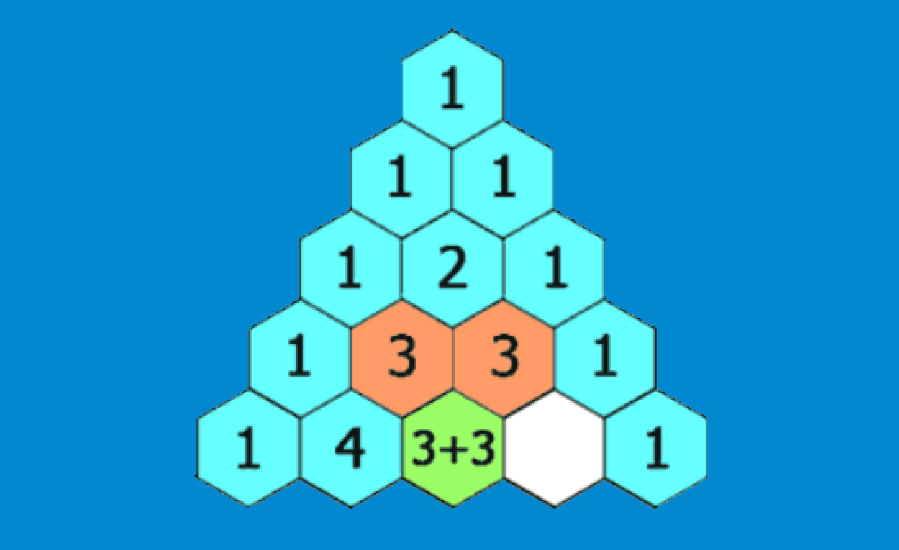
Uma alternativa para encontrar os coeficientes dos termos em uma expansão binomial é o triângulo de Pascal. O triângulo de Pascal é particularmente útil para expansões binomiais com coeficientes pequenos.
As linhas no triângulo de Pascal são numeradas começando com a linha $latex n=0$ no topo. Na linha 0, temos apenas o número 1. Para construir os elementos das linhas seguintes, adicionamos os dois números que estão acima para formar o novo valor. Quando não temos números no topo, substituímos por zero. Por exemplo, cada número na linha 1 é 0+1=1.
Como usar o teorema de Newton?
Para usar o teorema de Newton para expandir um binomial da forma $latex {{(a+b)}^n}$, precisamos lembrar o seguinte:
- Os expoentes do primeiro termo (a) diminuem de n para zero.
- Os expoentes do segundo termo (b) aumentam de zero para n.
- A soma dos expoentes de aeb é igual a n.
- Os coeficientes do primeiro e do último termo são ambos iguais a 1.
Vamos usar o teorema binomial para expandir várias expressões e entender o teorema:
EXERCÍCIO 1
Expanda o binômio $latex {{(x+y)}^5}$ usando o triângulo de Pascal.
Solução: Podemos ver que a linha 5 do triângulo de Pascal é 1, 5, 10, 10, 5, 1. Usando esses números para a expansão binomial, temos:
$${{(x+y)}^5}={{x}^5}+5{{x}^4}y+10{{x}^3}{{y}^2}+10{{x}^2}{{y}^3}+5x{{y}^4}+{{y}^5}$$
EXERCÍCIO 2
Expanda o binômio $latex {{(x+y)}^4}$ usando combinatória.
Solução: Isso pode ser expandido da seguinte forma:
$latex =\left( {\begin{array}{*{20}{c}} 4 \\ 0 \end{array}} \right){{x}^{4}}+\left( {\begin{array}{*{20}{c}} 4 \\ 1 \end{array}} \right){{x}^{3}}y+\left( {\begin{array}{*{20}{c}} 4 \\ 2 \end{array}} \right){{x}^{2}}{{y}^{2}}$ $latex +\left( {\begin{array}{*{20}{c}} 4 \\ 3 \end{array}} \right)x{{y}^{3}}+\left( {\begin{array}{*{20}{c}} 4 \\ 4 \end{array}} \right){{y}^{4}}$
Lembramos que tanto $latex \left( {\begin{array}{*{20}{c}} 4 \\ 0 \end{array}} \right)$ quanto $latex \left( {\begin{array}{*{20}{c}} 4 \\ 4 \end{array}} \right)$ são equivalentes a 1, pois só há uma maneira de escolher 0 e 4 elementos de um conjunto de 4 elementos. Então nós temos:
$$={{x}^{4}}+\left( {\begin{array}{*{20}{c}} 4 \\ 1 \end{array}} \right){{x}^{3}}y+\left( {\begin{array}{*{20}{c}} 4 \\ 2 \end{array}} \right){{x}^{2}}{{y}^{2}}+\left( {\begin{array}{*{20}{c}} 4 \\ 3 \end{array}} \right)x{{y}^{3}}+{{y}^{4}}$$
Agora avaliamos cada uma das combinações combinatórias restantes:
$latex \left( {\begin{array}{*{20}{c}} 4 \\ 1 \end{array}} \right)=\frac{{4!}}{{1!\left( {4-1} \right)!}}=\frac{{4!}}{{1!\left( 3 \right)!}}=4$
$latex \left( {\begin{array}{*{20}{c}} 4 \\ 2 \end{array}} \right)=\frac{{4!}}{{2!\left( {4-2} \right)!}}=\frac{{4!}}{{2!\left( 2 \right)!}}=6$
$latex \left( {\begin{array}{*{20}{c}} 4 \\ 3 \end{array}} \right)=\frac{{4!}}{{3!\left( {4-3} \right)!}}=\frac{{4!}}{{3!\left( 1 \right)!}}=4$
Ao substituir esses números na expressão, temos:
$latex {{x}^4}+4{{x}^3}y+6{{x}^2}{{y}^2}+4x{{y}^3}+{{y}^4}$
Como calcular um termo no binômio de Newton?
Pode haver momentos em que queremos identificar um termo específico na expansão de $latex {{(x+y)}^n}$. Isso é fácil quando temos n pequeno, mas quando temos binômios como $latex {{(x+y)}^9}$, isso é mais desafiador. Felizmente, podemos usar uma fórmula para isso. O termo r da expansão binomial pode ser encontrado com a fórmula:
$latex \left( {\begin{array}{*{20}{c}} n \\ {r-1} \end{array}} \right){{a}^{{n-\left( {r-1} \right)}}}{{b}^{{r-1}}}$
EXERCÍCIO
Encontre o quinto termo de $latex {{(3x-4)}^{{12}}}$.
Solução: Aqui temos $latex n=12$. Usamos $latex r=5$ já que estamos procurando o quinto termo. Usando a fórmula com esses valores, temos:
$latex \left( {\begin{array}{*{20}{c}} 12 \\ {5-1} \end{array}} \right){{3x}^{{12-\left( {5-1} \right)}}}{{(-4)}^{{5-1}}}$
$latex \left( {\begin{array}{*{20}{c}} {12} \\ 4 \end{array}} \right){{\left( {3x} \right)}^{8}}{{\left( {-4} \right)}^{4}}$
Podemos encontrar o valor de $latex \left( {\begin{array}{*{20}{c}} {12} \\ 4 \end{array}} \right)$ usando a fórmula combinatória:
$latex \frac{{n!}}{{\left( {n-k} \right)!k!}}=\frac{{12!}}{{\left( {12-4} \right)!4!}}$
$latex =495$
Então, temos:
$latex 495{{(3x)}^8}{{(-4)}^4}$
Expandindo isso totalmente, temos:
$latex 831409920{{x}^8}$
Veja também
Você quer aprender mais sobre fatoração de polinômios? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
