A excentricidade é uma característica que determina a forma das seções cônicas. A excentricidade das hipérboles depende do comprimento do eixo transversal e do comprimento do eixo conjugado. Por outro lado, o comprimento desses eixos pode ser encontrado diretamente na equação de uma hipérbole ou usando as coordenadas dos vértices e dos focos.
A seguir, aprenderemos sobre a equação que podemos usar para encontrar o valor da excentricidade das hipérboles. Em seguida, veremos alguns exercícios práticos.
PRÉ-CÁLCULO
Relevante para…
Aprender sobre a excentricidade da hipérbole com exercícios.
PRÉ-CÁLCULO
Relevante para…
Aprender sobre a excentricidade da hipérbole com exercícios.
Como calcular a excentricidade das hipérboles?
A excentricidade de uma hipérbole é calculada usando o comprimento do eixo transversal e o comprimento do eixo conjugado. Lembre-se de que as hipérboles são definidas como o conjunto de pontos em um plano, que têm uma diferença constante das distâncias dos dois focos. Isso resulta na excentricidade das hipérboles sempre maior que 1, ou seja, temos $latex e> 1$.
A equação geral de uma hipérbole é:
$latex \frac{{{x}^2}}{{{a}^2}}-\frac{{{y}^2}}{{{b}^2}}=1$
A fórmula de excentricidade é:
$latex e=\sqrt{1+\frac{{{b}^2}}{{{a}^2}}}$
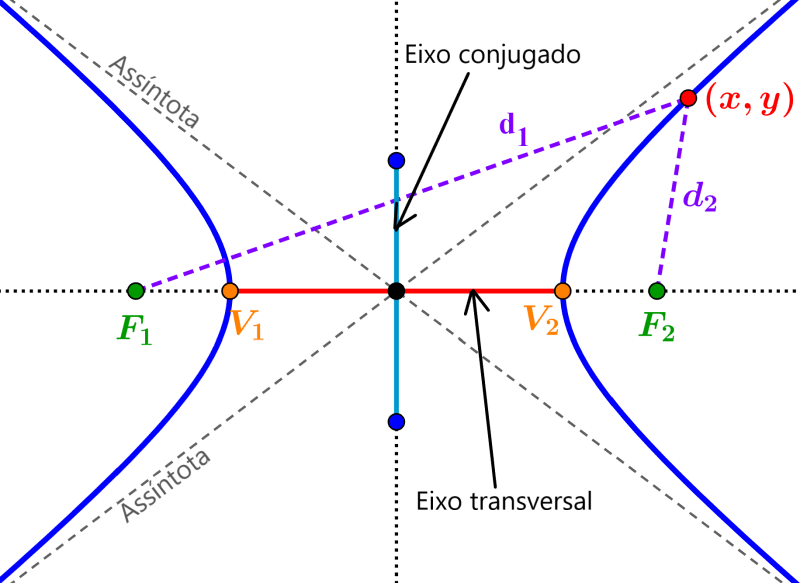
onde, a é o comprimento do eixo conjugado e b é o comprimento do eixo transversal. O eixo conjugado é o segmento que conecta os vértices e o eixo transversal é o segmento que conecta os co-vértices.
Além disso, também podemos calcular a excentricidade de uma hipérbole, usando a seguinte fórmula:
$latex e=\frac{c}{a}$
onde, c é o comprimento do segmento conectando os focos e pode ser calculado usando a equação $latex {{c}^2} = {{a}^2} + {{b}^2}$.
Exercícios de excentricidade de hipérbole resolvidos
Os exercícios a seguir são resolvidos usando a fórmula da excentricidade das hipérboles. Cada exercício tem sua respectiva resposta, mas é recomendável que você tente resolvê-los antes de procurar a solução.
EXERCÍCIO 1
Se uma hipérbole tem a equação $latex \frac{{{x}^2}}{25} – \frac{{{y}^2}}{16} = 1$, qual é a excentricidade?
Solução
Vemos que a equação tem a forma $latex \frac{{{x}^2}}{{{a}^2}}-\frac{{{y}^2}}{{{b}^2}}=1$, então, podemos obter os seguintes valores:
$latex {{a}^2}=25$
$latex {{b}^2}=16$
Agora, usamos esses valores na fórmula de excentricidade:
$latex e=\sqrt{1+\frac{{{b}^2}}{{{a}^2}}}$
$latex e=\sqrt{1+\frac{16}{25}}$
$latex e=1,28$
EXERCÍCIO 2
Temos a hipérbole $latex \frac{{{x}^2}}{64} – \frac{{{y}^2}}{25} = 1$. Qual é a sua excentricidade?
Solução
Novamente, temos uma equação com a mesma forma da anterior, para que possamos reconhecer os seguintes valores:
$latex {{a}^2}=64$
$latex {{b}^2}=25$
Usando esses valores na fórmula de excentricidade, temos:
$latex e=\sqrt{1+\frac{{{b}^2}}{{{a}^2}}}$
$latex e=\sqrt{1+\frac{25}{64}}$
$latex e=1,18$
EXERCÍCIO 3
Qual é a excentricidade da hipérbole $latex \frac{{{x}^2}}{121} – \frac{{{y}^2}}{81} = 1$?
Solução
Temos que determinar os valores de $latex {{a}^2}$ e $latex {{b}^2}$. Então, temos:
$latex {{a}^2}=121$
$latex {{b}^2}=81$
Usamos a fórmula de excentricidade com estes valores:
$latex e=\sqrt{1+\frac{{{b}^2}}{{{a}^2}}}$
$latex e=\sqrt{1+\frac{81}{121}}$
$latex e=1,2$
EXERCÍCIO 4
Se uma hipérbole tem a equação $latex \frac{{{x}^2}}{120} – \frac{{{y}^2}}{40} = 1$, qual é sua excentricidade?
Solução
Reconhecemos os seguintes valores observando a equação da hipérbole:
$latex {{a}^2}=120$
$latex {{b}^2}=40$
Agora, substituímos esses valores na fórmula de excentricidade e resolvemos:
$latex e=\sqrt{1+\frac{{{b}^2}}{{{a}^2}}}$
$latex e=\sqrt{1+\frac{40}{120}}$
$latex e=1,15$
Exercícios de excentricidade de hipérbole para resolver
Pratique o uso da fórmula de excentricidade da hiperbola resolvendo os exercícios a seguir. Selecione uma resposta e verifique se você obteve a resposta correta.
Veja também
Você quer aprender mais sobre hipérboles? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
