As hipérboles são seções cônicas formadas quando um plano cruza um par de cones. As hipérboles têm a característica de que a diferença das distâncias de qualquer ponto da curva aos dois focos é igual a uma constante. As hipérboles são compostas por dois ramos de formato parabólico. Todas as hipérboles têm duas linhas de simetria, que se cruzam no centro.
A seguir, veremos uma definição mais detalhada de hipérboles e aprenderemos sobre algumas de suas características mais importantes.
PRÉ-CÁLCULO
Relevante para…
Conhecer as características importantes das hipérboles.
PRÉ-CÁLCULO
Relevante para…
Conhecer as características importantes das hipérboles.
Definição de uma hipérbole
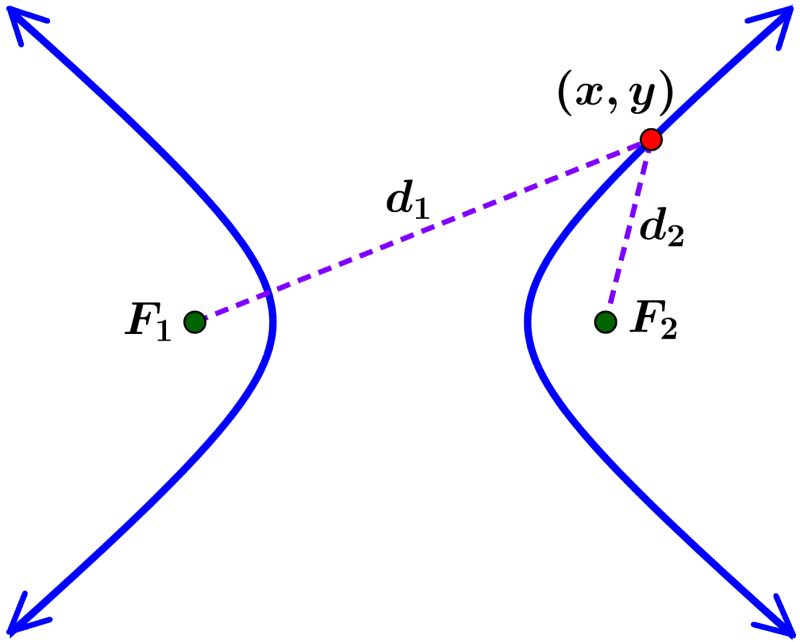
Uma hipérbole é definida como o conjunto de pontos de modo que a diferença das distâncias aos dois focos seja uma constante. As hipérboles são compostas por dois ramos, que são um reflexo um do outro. Cada ramo da hipérbole é semelhante a uma parábola e tem um foco e um vértice.
As hipérboles também são definidas como seções cônicas obtidas na interseção de um plano com um par de cones. O plano corta ambas as bases dos cones em um determinado ângulo.
Principais características da hipérbole
As principais características de uma hipérbole são:
- As hipérboles têm dois pontos focais, chamados focos.
- A excentricidade das hipérboles é maior que 1.
- A diferença de cada distância de um ponto da hipérbole aos dois focos é constante.
- As hipérboles têm dois eixos de simetria, um eixo passa pelos focos e o outro eixo é perpendicular ao primeiro.
- A intersecção das linhas de simetria é o centro da hipérbole.
- As hipérboles têm duas assíntotas, das quais se aproximam, mas nunca se tocam.
- As assíntotas também se cruzam no centro da hipérbole.
Equação de hipérbole
A forma da equação da hipérbole depende se a hipérbole está centrada na origem ou fora da origem.
Quando temos uma hipérbole centrada na origem, sua equação geral é:
| $latex \frac{{{x}^2}}{{{a}^2}}-\frac{{{y}^2}}{{{b}^2}}=1$ |
onde, a representa o comprimento do segmento que se estende entre os dois vértices da hipérbole e b é encontrado com a equação $latex {{b}^2}={{a}^2}({{e}^2}-1)$, onde, e é excentricidade.
Se o centro da hipérbole estiver localizado fora da origem, a equação da hipérbole é:
| $latex \frac{{{(x-h)}^2}}{{{a}^2}}-\frac{{{(y-k)}^2}}{{{b}^2}}=1$ |
onde, $latex (h, k)$ são as coordenadas do centro da hipérbole.
Veja também
Você quer aprender mais sobre hipérboles? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
