A parábola é uma seção cônica que se forma quando um cone é cortado por um plano paralelo a um dos lados do cone. A parábola tem como característica principal que todos os seus pontos estão à mesma distância de um ponto denominado foco e de uma reta denominada diretriz. Outros elementos importantes de uma parábola são o vértice, o eixo, o lado reto e o comprimento focal.
A seguir, aprenderemos mais sobre esses elementos e usaremos diagramas para ilustrá-los. Além disso, conheceremos os diferentes tipos de parábolas que podemos ter.
Definição de parábola
Uma parábola é definida como uma seção cônica. As parábolas são obtidas cortando um cone com um plano paralelo a um dos lados do cone. As parábolas são formadas por um conjunto de pontos que se caracterizam por terem a mesma distância de um ponto fixo, denominado foco, e de uma linha reta, denominada diretriz.
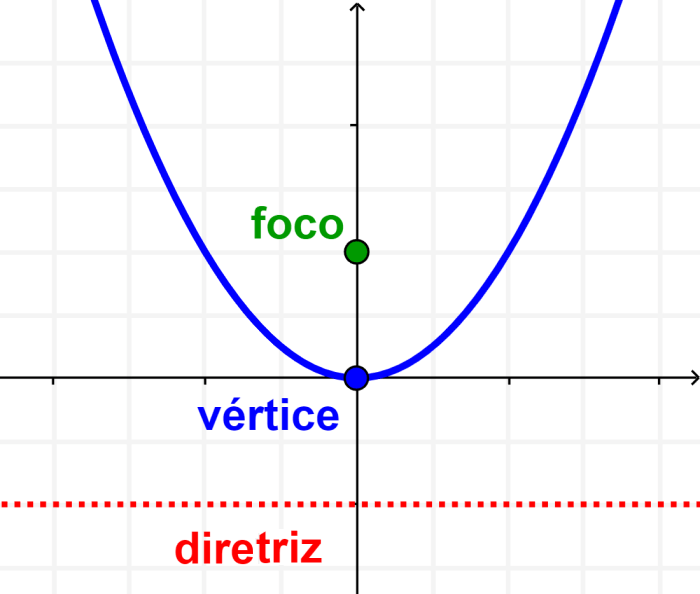
Elementos fundamentais de uma parábola
A seguir estão os elementos fundamentais de uma parábola:
- Vértice
- Foco
- Comprimento focal
- Lado reto
- Diretriz
- Eixo
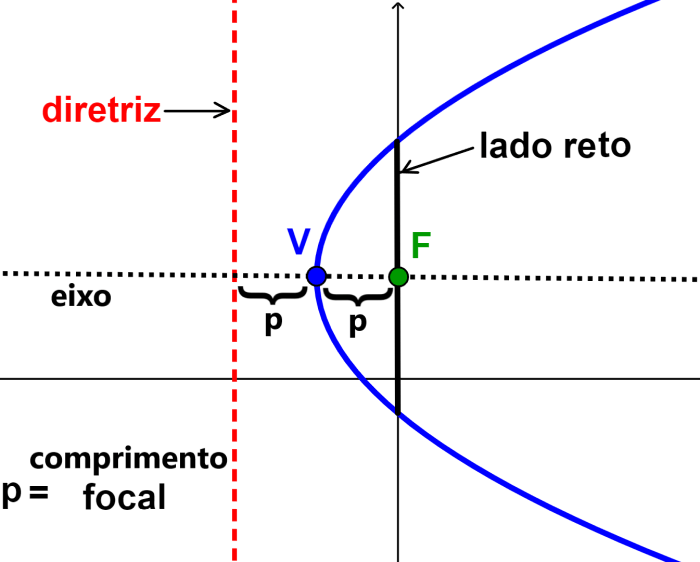
Vértice
O vértice da parábola é seu ponto extremo. Se a parábola abre para cima, o vértice representa o ponto mais baixo da parábola. Se a parábola abre para baixo, o vértice representa o ponto mais alto. Em ambos os casos, o vértice é um ponto que muda a direção da parábola.
Freqüentemente, o vértice é representado pelo V.
Foco
O foco é um ponto fixo usado para definir a parábola. Este ponto não está localizado na parábola, mas no interior. O foco é denotado por F.
Comprimento focal
O comprimento focal é o comprimento entre o vértice e o foco.
Lado reto
O lado reto é uma linha perpendicular à linha que une o vértice e o foco e tem quatro vezes o comprimento do comprimento focal.
Diretriz
A diretriz é uma linha reta na frente da parábola. Usamos d para representar a diretriz. A distância entre a diretriz e o vértice é igual à distância entre o foco e o vértice.
Eixo
O eixo da parábola é uma linha perpendicular à diretriz. O eixo representa a linha de simetria da parábola.
Tipos de parábolas
Podemos classificar as parábolas de acordo com sua orientação. Podemos ter parábolas orientadas horizontalmente e verticalmente. Além disso, as parábolas podem ser abertas para a direita, para a esquerda, para cima e para baixo.
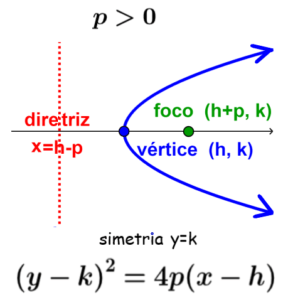
Parábola horizontal que se abre para a direita
Esta parábola é obtida quando a diretriz é vertical e o parâmetro p é positivo.
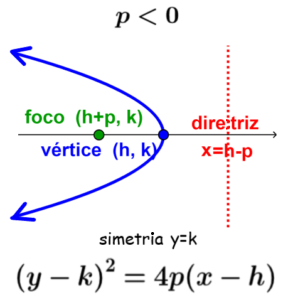
Parábola horizontal que se abre para a esquerda
Esta parábola é obtida quando a diretriz é vertical e o parâmetro p é negativo.
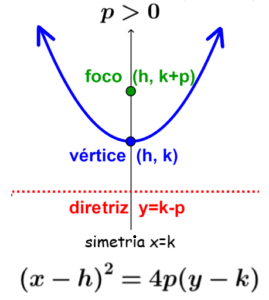
Parábola vertical que se abre para cima
Essa parábola é obtida quando a diretriz é horizontal e o parâmetro p é positivo.
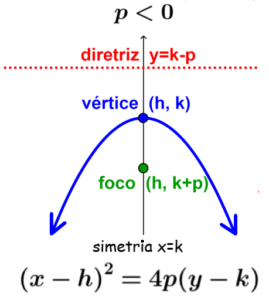
Parábola vertical que se abre para baixo
Essa parábola é obtida quando a diretriz é horizontal e o parâmetro p é negativo.
Veja também
Você quer aprender mais sobre equações de parábolas? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
