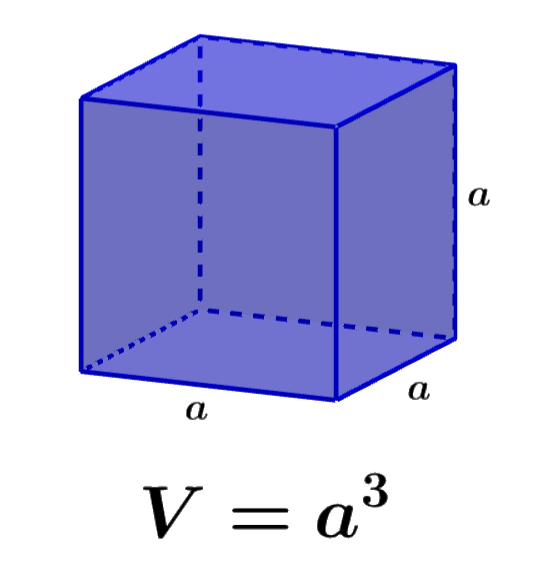
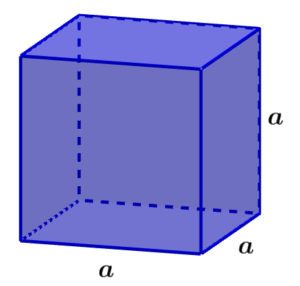
O volume de um cubo define o número de unidades cúbicas que são completamente ocupadas pelo cubo. Um cubo é uma figura tridimensional sólida com seis faces quadradas. Para calcular o volume, precisamos saber a dimensão de seus lados. Como um cubo tem todos os lados do mesmo comprimento, podemos encontrar o volume do cubo elevando um de seus lados à potência de 3.
A seguir, saberemos a fórmula que podemos usar para encontrar o volume dos cubos. Aprenderemos a derivar essa fórmula e usá-la para resolver alguns exercícios.
Fórmula para o volume de um cubo
Podemos calcular facilmente o volume dos cubos se soubermos o comprimento de um de seus lados. O volume é o produto do comprimento, largura e altura. No caso dos cubos, sabemos que todos os seus lados têm comprimentos iguais, então temos:
Volume = Comprimento × Largura × Altura
$latex V=a\times a \times a$
| $latex V={{a}^3}$ |
onde, a é o comprimento de um dos lados do cubo.
Derivação da fórmula do volume
Sabemos que um cubo é um objeto tridimensional que possui comprimento, largura e altura com o mesmo comprimento. Podemos derivar sua fórmula de volume da seguinte forma :
- Vamos considerar uma folha quadrada de papel.
- A área dessa folha quadrada será igual ao seu comprimento multiplicado pela sua largura.
- Como o comprimento e a largura são iguais em um quadrado, sua área será $latex {{a}^2}$.
- Um cubo é formado empilhando várias folhas de papel umas sobre as outras até obter uma altura igual a a.
- Podemos concluir que o volume coberto pelo cubo é igual à área da base multiplicada pela altura.
- Então, o volume do cubo é igual a $latex {{a}^3}$.
Volume de um cubo usando a diagonal
Também é possível calcular o volume de um cubo usando o comprimento da diagonal. Para isso, podemos usar a seguinte fórmula:
| $latex V=\sqrt{3} \times \frac{{{d}^3}}{9}$ |
onde, d é o comprimento da diagonal de um cubo.
Exercícios de volume de um cubo resolvidos
Os exercícios a seguir podem ser usados para praticar a aplicação das fórmulas para o volume dos cubos. Cada exercício tem sua respectiva solução, onde são detalhados o processo e o raciocínio utilizado.
EXERCÍCIO 1
Qual é o volume de um cubo com lados de 5 m de comprimento?
Solução
Podemos usar a fórmula do primeiro volume com o comprimento $latex a = 5$. Então, temos:
$latex V=a^3$
$latex V={{5}^3}$
$latex V=125$
O volume é igual a 125 m³.
EXERCÍCIO 2
Se um cubo tem lados com comprimento de 10 m, qual é o seu volume?
Solução
Temos o comprimento $latex a = 10$, portanto, substituímos esse valor na fórmula do volume:
$latex V=a^3$
$latex V={{10}^3}$
$latex V=1000$
O volume é igual a 1000 m³.
EXERCÍCIO 3
Um cubo tem um volume de 512 cm³. Qual é o comprimento de um de seus lados?
Solução
Neste caso, começamos com a área e queremos encontrar o comprimento de um dos lados. Usamos a fórmula do volume e resolvemos para a:
$latex V=a^3$
$latex 512={{a}^3}$
$latex a=8$
O comprimento de um dos lados é de 8 cm³.
EXERCÍCIO 4
Qual é o volume de um cubo com diagonal de 5 m?
Solução
Aqui, temos o comprimento $latex d = 5$, então usamos a segunda fórmula com este valor:
$latex V=\sqrt{3}\times \frac{{{d}^3}}{9}$
$latex V=\sqrt{3}\times \frac{{{5}^3}}{9}$
$latex V=\sqrt{3}\times \frac{125}{9}$
$latex V=24,1$
O volume é igual a 24,1 m³.
EXERCÍCIO 5
Um cubo tem diagonal de 10 m. Qual é o seu volume?
Solução
Usamos a segunda fórmula da área com $latex l=10$:
$latex A=2(1+\sqrt{2}){{l}^2}$
$latex A=2(1+\sqrt{2}){{(10)}^2}$
$latex A=2(1+\sqrt{2})(100)$
$latex A=482,84$
A área do octógono é de 482,84 m².
Exercícios de volume de um cubo para resolver
Ponha em prática as fórmulas para o volume de cubos vistas acima para resolver os exercícios seguintes. Se precisar de ajuda com isso, você pode consultar os exercícios resolvidos acima.
Veja também
Você quer aprender mais sobre cubos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
