O cubo é um dos objetos sólidos tridimensionais mais comuns. A principal característica dos cubos é que possuem todas as faces com o mesmo comprimento. Os cubos têm 6 faces, 12 arestas e 8 vértices. Essas figuras têm exemplos muito comuns na vida real, como o cubo de Rubik e um dado padrão de 6 lados.
A seguir, veremos uma definição mais detalhada de cubos e usaremos diagramas para ilustrar os conceitos. Além disso, conheceremos as características mais importantes dos cubos. Finalmente, veremos as fórmulas mais importantes dessas figuras geométricas e as usaremos para resolver alguns exercícios.
Definição de um cubo
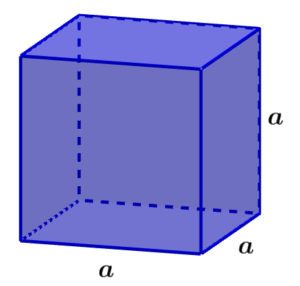
O cubo é um objeto sólido tridimensional delimitado por seis faces quadradas. Três dessas faces se encontram em cada vértice. O cubo também é definido como um hexaedro, ou seja, um sólido com seis faces. Os cubos são um tipo de prismas quadrados.
Muitas vezes, a forma de um cubo é considerada um bloco, onde comprimento, altura e largura são iguais. Além disso, uma característica principal dos cubos é que eles têm 6 faces, 8 vértices e 12 arestas.
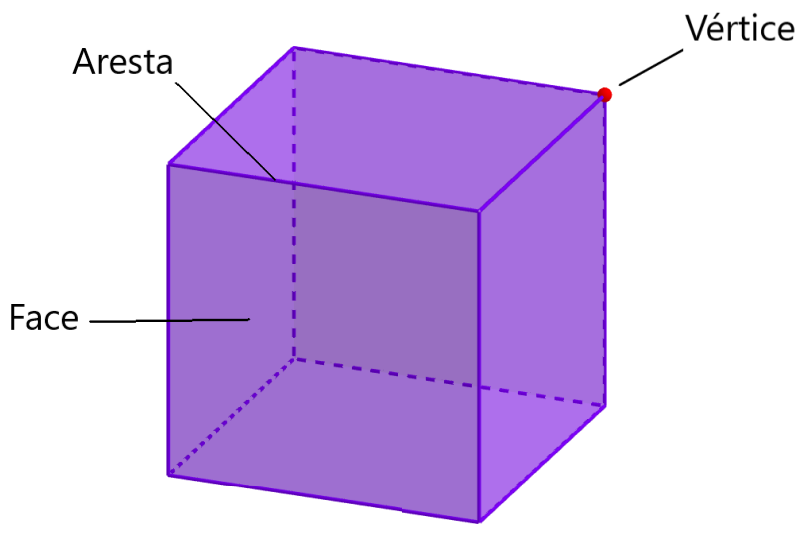
Podemos distinguir esses elementos no diagrama a seguir.
Na imagem podemos ver o vértice, a face e a aresta. As faces do cubo são conectadas por quatro vértices. As arestas do cubo são conectadas em um único ponto, que é o vértice.
Como o cubo é uma figura 3D, os dois parâmetros importantes usados para medir o cubo são o volume e a área da superfície.
Características fundamentais de um cubo
A seguir estão as características mais importantes dos cubos:
- Todos os suas faces têm formato quadrado.
- Todas as faces e lados têm dimensões iguais.
- Cada uma das faces encontra quatro faces.
- Os ângulos internos do cubo são ângulos retos.
- Cada um dos vértices encontra três faces e três arestas.
- As arestas opostas são paralelas.
Fórmulas importantes de um cubo
As fórmulas de cubo mais importantes para resolver exercícios são a fórmula do volume, a fórmula da área de superfície e a fórmula diagonal.
Fórmula de volume de cubos
O volume de um cubo pode ser calculado multiplicando os comprimentos de suas três dimensões. Como todos os lados têm a mesma medida, temos:
| $latex V={{a}^3}$ |
onde, a representa o comprimento de um dos lados.
Fórmula para área de cubos
A área de cubos é a soma das áreas de todas as faces do cubo. Sabemos que temos seis faces iguais em um cubo e também que a área de uma face é igual à área de um quadrado, então temos:
| $latex A_{s}=6{{a}^2}$ |
onde, a é o comprimento de um dos lados.
Fórmula da diagonal de cubos
A fórmula para a diagonal de um cubo é derivada usando o teorema de Pitágoras duas vezes. Então, para simplificar, temos a seguinte expressão:
| $latex d=\sqrt{3}~a$ |
onde, d representa o comprimento da diagonal e a representa o comprimento de um dos lados.
Exemplos de problemas de cubos
EXEMPLO 1
Qual é o volume de um cubo que tem lados de 8 m de comprimento?
Solução: Usamos o comprimento $latex a = 8$ na fórmula do volume. Então, temos:
$latex V={{a}^3}$
$latex V={{8}^3}$
$latex V=512$
O volume do cubo é 512 m³.
EXEMPLO 2
Um cubo tem lados de 10 m de comprimento. Qual é a sua área de superfície?
Solução: Temos o comprimento $latex a = 10$, então usamos este valor na fórmula para a área do cubo:
$latex A_{s}=6{{a}^2}$
$latex A_{s}=6{{(10)}^2}$
$latex A_{s}=6(100)$
$latex A_{s}=600$
A área do cubo é de 600 m².
EXEMPLO 3
Se um cubo tem lados com comprimento de 20 m, qual é o comprimento de sua diagonal?
Solução: Usamos o comprimento $latex a = 20$ na fórmula diagonal. Então, temos:
$latex d=\sqrt{3}~a$
$latex d=\sqrt{3}(20)$
$latex d=34,64$
O comprimento da diagonal é de 34,64 m.
Veja também
Você quer aprender mais sobre cubos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
