O volume de uma pirâmide hexagonal é encontrado multiplicando a área da base hexagonal pela altura da pirâmide e dividindo por três. Para calcular a área, temos de somar as áreas de todas as faces da pirâmide.
A seguir, vamos aprender as fórmulas que podemos usar para calcular o volume e a área das pirâmides hexagonais. Depois, aplicaremos esta fórmula para resolver alguns exercícios práticos.
GEOMETRIA
Relevante para…
Aprender a calcular o volume e área de uma pirâmide hexagonal.
GEOMETRIA
Relevante para…
Aprender a calcular o volume e área de uma pirâmide hexagonal.
Como calcular o volume de uma pirâmide hexagonal
Uma pirâmide é uma figura tridimensional composta por uma base e faces laterais que se encontram em um único ponto acima. O volume dessas figuras é encontrado multiplicando a área de sua base pela altura e dividindo por três. Portanto, temos a seguinte fórmula:
$latex \text{Volume} = \frac{1}{3}\text{Base} \times \text{Altura}$
As pirâmides hexagonais têm um hexágono como base, então temos que encontrar uma expressão para a área de um hexágono. A área de um hexágono é calculada usando seu apótema e o comprimento de um de seus lados.
No entanto, também é possível encontrar a área dos hexágonos simplesmente usando o comprimento de um de seus lados. Para isso, usamos a seguinte fórmula:
$latex A= \frac{3\sqrt{3}}{2}{{l}^2}$
onde, l representa o comprimento de um dos lados do hexágono.
Se substituirmos esta expressão na fórmula para o volume de uma pirâmide, temos:
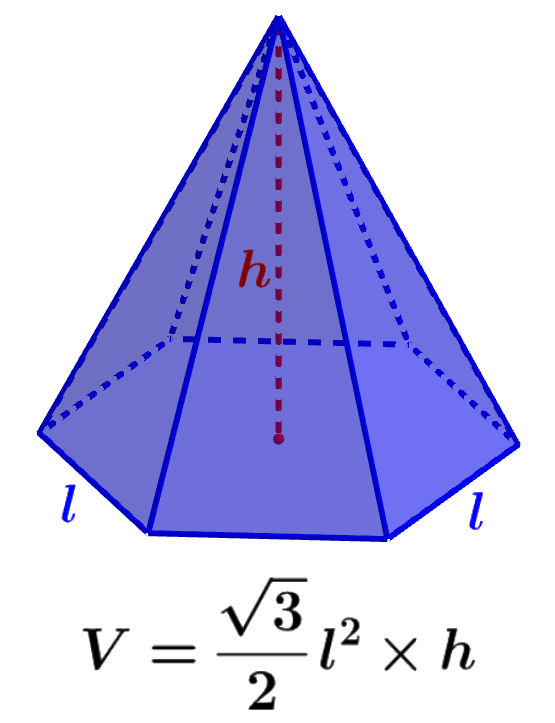
$latex V=\frac{1}{3}\times \frac{3\sqrt{3}}{2}{{l}^2}\times h$
| $latex V=\frac{\sqrt{3}}{2}{{l}^2}\times h$ |
onde, l é o comprimento de um dos lados da base hexagonal e h é o comprimento da altura da pirâmide.
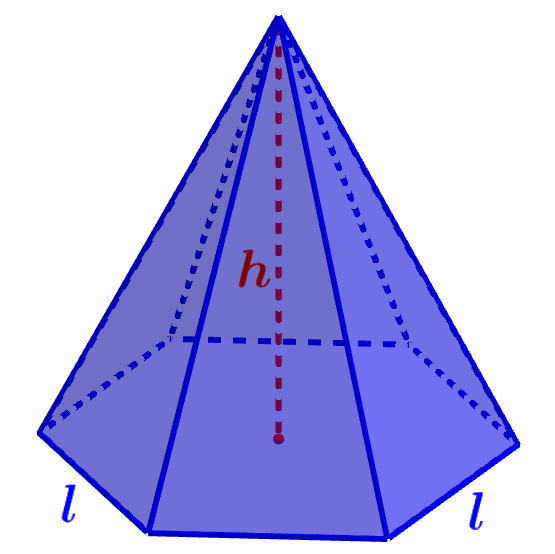
Como calcular a área da pirâmide hexagonal
A área de uma figura 3D é encontrada somando as áreas de todas as faces da figura tridimensional. Estas pirâmides têm uma face hexagonal e seis faces triangulares laterais.
A área da base hexagonal é encontrada usando a fórmula para a área de um hexágono:
$latex A=\frac{3\sqrt{3}}{2}{{l}^2}$
onde, l representa o comprimento de um dos lados do hexágono.
Por outro lado, a área das faces triangulares é encontrada usando a fórmula para a área de qualquer triângulo:
$latex A=\frac{1}{2}b\times h$
onde, b é o comprimento da base do triângulo e h é o comprimento da altura do triângulo.
Em uma pirâmide hexagonal, a base das faces triangulares é igual aos lados da base hexagonal. Além disso, considerando que as seis faces triangulares são iguais, temos a seguinte fórmula para a área das pirâmides hexagonais:
$latex A_{s}=\frac{3\sqrt{3}}{2}{{l}^2}+6(\frac{1}{2}b\times h)$
$latex A_{s}=\frac{3\sqrt{3}}{2}{{l}^2}+3lh)$
Exercícios de volume e área de pirâmides hexagonais resolvidos
EXERCÍCIO 1
Se uma pirâmide tem uma altura de 4 m e uma base hexagonal com lados de 1 m, qual é o seu volume?
Solução
Temos as seguintes informações:
- Altura, $latex h=4$
- Lados de hexágono, $latex l=1$
Temos que usar esses valores na fórmula de volume:
$latex V=\frac{\sqrt{3}}{2}{{l}^2}\times h$
$latex V=\frac{\sqrt{3}}{2}{{(1)}^2}\times (4)$
$latex V=\frac{\sqrt{3}}{2}(4)$
$latex V=3,46$
O volume é igual a 3,46 m³.
EXERCÍCIO 2
Se uma pirâmide tem uma base hexagonal com lados de 1 m de comprimento e suas faces triangulares de 3 m de altura, qual é sua área?
Solução
Temos os comprimentos $latex l = 1$ e $latex h = 3$. Então, usamos a fórmula para área da pirâmidecom esses valores:
$latex A_{s}=\frac{3\sqrt{3}}{2}{{l}^2}+3lh$
$latex A_{s}=\frac{3\sqrt{3}}{2}{{(1)}^2}+3(1)(3)$
$latex A_{s}=\frac{3\sqrt{3}}{2}(1)+9$
$latex A_{s}=2,6+9$
$latex A_{s}=11,6$
A área da pirâmide é igual a 11,6 m².
EXERCÍCIO 3
Qual é o volume de uma pirâmide de 5 m de altura e base hexagonal com lados de 2 m?
Solução
Temos os seguintes dados:
- Altura, $latex h=5$
- Lados de hexágono, $latex l=2$
Usamos a fórmula de volume com estes dados:
$latex V=\frac{\sqrt{3}}{2}{{l}^2}\times h$
$latex V=\frac{\sqrt{3}}{2}{{(2)}^2}\times (5)$
$latex V=\frac{\sqrt{3}}{2}(20)$
$latex V=17,32$
O volume é igual a 17,32 m³.
EXERCÍCIO 4
Se uma pirâmide tem uma base hexagonal com lados de 2 m e faces triangulares de 5 m de altura, qual é sua área?
Solução
Temos os valores $latex l = 2$ e $latex h = 5$. Usando esses valores na fórmula para área da pirâmide, temos:
$latex A_{s}=\frac{3\sqrt{3}}{2}{{l}^2}+3lh$
$latex A_{s}=\frac{3\sqrt{3}}{2}{{(2)}^2}+3(2)(5)$
$latex A_{s}=\frac{3\sqrt{3}}{2}(4)+30$
$latex A_{s}=10,4+30$
$latex A_{s}=40,4$
A área da pirâmide é igual a 40,4 m².
EXERCÍCIO 5
Se uma pirâmide hexagonal tem lados com 3 m de comprimento e 8 m de altura, qual é o seu volume?
Solução
Temos o seguinte:
- Altura, $latex h=8$
- Lados de hexágono, $latex l=3$
Usando a fórmula de volume com esses dados, temos:
$latex V=\frac{\sqrt{3}}{2}{{l}^2}\times h$
$latex V=\frac{\sqrt{3}}{2}{{(3)}^2}\times (8)$
$latex V=\frac{\sqrt{3}}{2}(72)$
$latex V=62,35$
O volume é igual a 62,35 m³.
EXERCÍCIO 6
Qual é a área de uma pirâmide hexagonal com lados de 4 m e faces triangulares de 6 m de altura?
Solução
Temos os comprimentos $latex l = 4$ e $latex h = 6$. Usando esses valores na fórmula, temos:
$latex A_{s}=\frac{3\sqrt{3}}{2}{{l}^2}+3lh$
$latex A_{s}=\frac{3\sqrt{3}}{2}{{(4)}^2}+3(4)(6)$
$latex A_{s}=\frac{3\sqrt{3}}{2}(16)+72$
$latex A_{s}=41,6+72$
$latex A_{s}=113,6$
A área da pirâmide é igual a 113,6 m².
EXERCÍCIO 7
Qual é a altura de uma pirâmide de 50 m³ de volume e base hexagonal com lados de 3 m de comprimento?
Solução
Temos as seguintes informações:
- Volume, $latex V=50$
- Lados de hexágono, $latex l=3$
Aqui, temos a medida do volume, mas temos que encontrar o comprimento da altura. Então, usamos a fórmula do volume e resolvemos para h :
$latex V=\frac{\sqrt{3}}{2}{{l}^2}\times h$
$latex 50=\frac{\sqrt{3}}{2}{{(3)}^2}\times h$
$latex 50=\frac{\sqrt{3}}{2}(9)\times h$
$latex 50=7,79 h$
$latex h\approx 6,42$
O comprimento da altura é igual a 6,42 m.
EXERCÍCIO 8
Se uma pirâmide tem uma base hexagonal com lados de 5 m de comprimento e suas faces triangulares de 10 m de altura, qual é sua área?
Solução
Temos os comprimentos $latex l = 5$ e $latex h = 10$. Então, usamos a fórmula para área da pirâmide com estes valores:
$latex A_{s}=\frac{3\sqrt{3}}{2}{{l}^2}+3lh$
$latex A_{s}=\frac{3\sqrt{3}}{2}{{(5)}^2}+3(5)(10)$
$latex A_{s}=\frac{3\sqrt{3}}{2}(25)+150$
$latex A_{s}=65+150$
$latex A_{s}=215$
A área da pirâmide é 215 m².
EXERCÍCIO 9
Se uma pirâmide tem um volume de 64 m³ e uma base hexagonal com lados de 4 m, qual é o comprimento de sua altura?
Solução
Temos o seguinte:
- Volume, $latex V=64$
- Lados de hexágono, $latex l=4$
Semelhante ao exercício anterior, usamos a fórmula do volume e resolvemos para h :
$latex V=\frac{\sqrt{3}}{2}{{l}^2}\times h$
$latex 64=\frac{\sqrt{3}}{2}{{(4)}^2}\times h$
$latex 64=\frac{\sqrt{3}}{2}(16)\times h$
$latex 64=13,86 h$
$latex h\approx 4,62$
O comprimento da altura é igual a 4,62 m.
Exercícios de volume e área de pirâmides hexagonais para resolver
Qual é a altura de uma pirâmide com um volume de 79,5 m3 e uma base hexagonal com lados de 3 m?
Escreva a resposta usando uma única casa decimal.
Veja também
Você quer aprender mais sobre pirâmides geométricas? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
