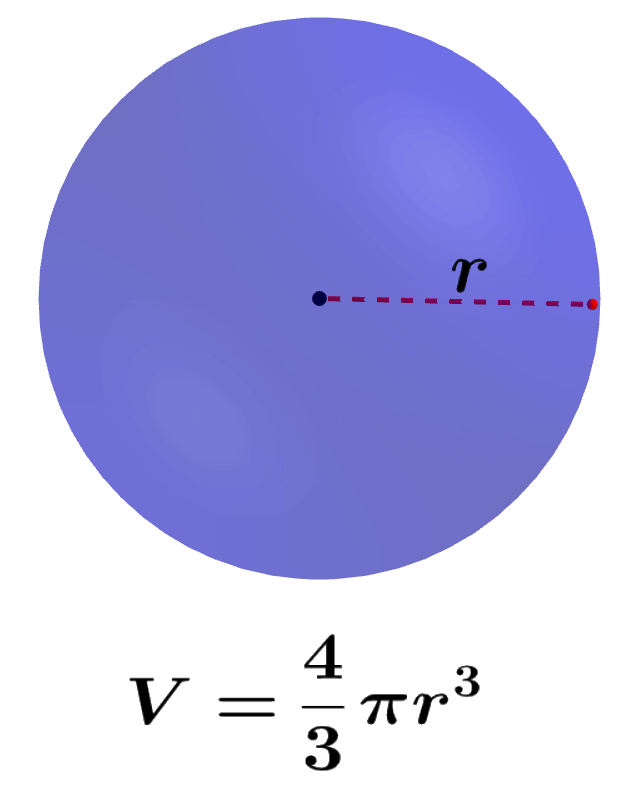
O volume de uma esfera é igual ao espaço ocupado pela esfera em todas as três dimensões. O volume de uma esfera depende de seu raio, pois, se tomarmos a seção transversal da esfera, temos um círculo. Portanto, temos que usar o comprimento do raio para calcular seu volume. Alternativamente, também podemos calcular seu volume usando o diâmetro, pois é simplesmente o dobro do raio.
A seguir, conheceremos as fórmulas que podemos usar para calcular o volume das esferas usando seu raio e diâmetro. Além disso, também aprenderemos a calcular o volume de esferas ocas. Finalmente, aplicaremos todas as fórmulas aprendidas para resolver alguns exercícios.
Fórmula para o volume da esfera
A esfera é definida como uma figura sólida tridimensional, em que cada ponto em sua superfície é equidistante do centro. A distância fixa é chamada de raio da esfera e o ponto fixo é chamado de centro da esfera.
O volume de uma esfera é determinado usando o comprimento do raio e a seguinte fórmula:
| $latex V=\frac{4}{3}\pi {{r}^3}$ |
onde, r é o comprimento do raio da esfera.
Esta fórmula é derivada usando métodos de integração.
Volume da esfera usando diâmetro
Alternativamente, podemos usar o diâmetro de uma esfera para calcular seu volume. Podemos fazer isso usando dois métodos diferentes.
O primeiro método é lembrar que o diâmetro de uma esfera é igual a 2r, onde r é o comprimento do raio da esfera. Portanto, se temos o comprimento do diâmetro, podemos dividir por dois para obter o comprimento do raio e usar a fórmula de volume fornecida acima.
O segundo método é escrever a fórmula do volume em termos do diâmetro da esfera. Se fizermos isso, teremos:
$latex V=\frac{4}{3}\pi {{r}^3}$
$latex V=\frac{4}{3}\pi {{(\frac{d}{2})}^3}$
$latex V=\frac{4}{3}\pi (\frac{{{d}^3}}{8})$
$latex V=\frac{4}{24}\pi {{d}^3}$
| $latex V=\frac{1}{6}\pi {{d}^3}$ |
onde, d é o comprimento do diâmetro.
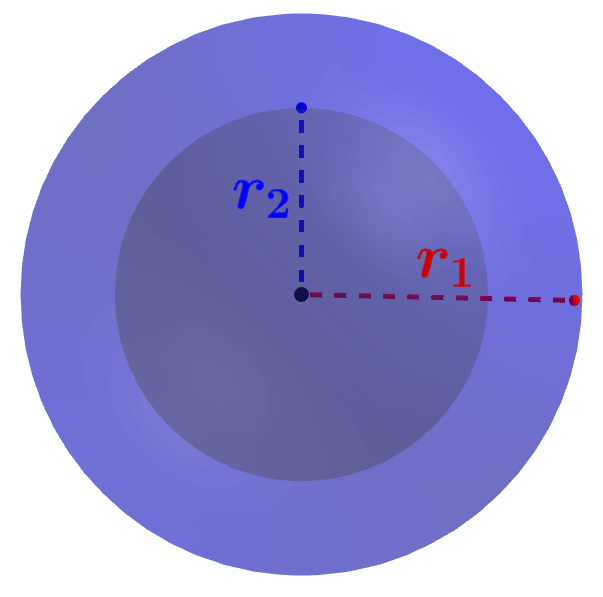
Volume da esfera oca
O volume das esferas ocas é calculado subtraindo o volume da parte oca do volume de toda a esfera. Portanto, se usarmos $latex r_{1}$ para representar o raio da esfera completa e $latex r_{2}$ para representar o raio interno, ou seja, o raio da parte oca, temos:
$latex V=\frac{4}{3}\pi {{r_{1}}^3}-\frac{4}{3}\pi {{r_{2}}^3}$
Podemos simplificar isso para obter a seguinte fórmula:
| $latex V=\frac{4}{3}\pi ({{r_{1}}^3}-{{r_{2}}^3})$ |
Exercícios de volume da esfera resolvidos
Os exercícios a seguir são resolvidos usando as fórmulas para o volume das esferas vistas acima. Cada exercício tem sua respectiva solução, onde são detalhados o processo e o raciocínio utilizado.
EXERCÍCIO 1
Qual é o volume de uma esfera com raio de 3 m?
Solução
Usamos a primeira fórmula do volume com $latex r=3$:
$latex V=\frac{4}{3}\pi {{r}^3}$
$latex V=\frac{4}{3}\pi {{(3)}^3}$
$latex V=\frac{4}{3}\pi (27)$
$latex V=113,1$
O volume é igual a 113,1 m³.
EXERCÍCIO 2
Uma esfera tem um raio de 4 m. Qual é o seu volume?
Solução
Temos que usar a primeira fórmula do volume com o comprimento $latex r=4$:
$latex V=\frac{4}{3}\pi {{r}^3}$
$latex V=\frac{4}{3}\pi {{(4)}^3}$
$latex V=\frac{4}{3}\pi (64)$
$latex V=268,1$
O volume é igual a 268,1 m³.
EXERCÍCIO 3
Qual é o volume de uma esfera com um diâmetro de 5 m?
Solução
Neste caso, temos o diâmetro da esfera, então temos que dividir por 2 e usar a fórmula do volume. Isso significa que o raio é $latex r=2,5$:
$latex V=\frac{4}{3}\pi {{r}^3}$
$latex V=\frac{4}{3}\pi {{(2.5)}^3}$
$latex V=\frac{4}{3}\pi (6.25)$
$latex V=26,2$
O volume é igual a 26,2 m³.
EXERCÍCIO 4
Qual é o volume de uma esfera oca que tem um raio externo de 6 m e um raio interno de 4 m?
Solução
Temos uma esfera oca com os raios $latex r_{1}=6$ e $latex r_{2}=4$. Então, usamos a fórmula do terceiro volume com estes raios:
$latex V=\frac{4}{3}\pi ({{r_{1}}^3}-{{r_{2}}^3})$
$latex V=\frac{4}{3}\pi ({{(6)}^3}-{{(4)}^3})$
$latex V=\frac{4}{3}\pi (216-64)$
$latex V=\frac{4}{3}\pi (152)$
$latex V=636,7$
O volume é igual a 636,7 m³.
EXERCÍCIO 5
Uma esfera oca tem um raio externo de comprimento de 5 m e um raio interno de comprimento de 4 m. Qual é o seu volume?
Solução
Os raios da esfera oca são $latex r_{1} = 5$ e $latex r_{2} = 4$. Então, usamos esses valores na fórmula para o volume de uma esfera oca:
$latex V=\frac{4}{3}\pi ({{r_{1}}^3}-{{r_{2}}^3})$
$latex V=\frac{4}{3}\pi ({{(5)}^3}-{{(4)}^3})$
$latex V=\frac{4}{3}\pi (125-64)$
$latex V=\frac{4}{3}\pi (152)$
$latex V=255,5$
O volume é igual a 255,5 m³.
Exercícios de volume da esfera para resolver
Ponha em prática o uso das fórmulas de volume vistas acima para resolver os seguintes exercícios. Selecione sua resposta e verifique se você obteve a resposta correta.
Veja também
Você quer aprender mais sobre esferas? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
