Um triângulo retângulo é um triângulo no qual exatamente um ângulo interno mede 90 graus. Como a soma dos ângulos internos em qualquer triângulo é igual a 180 graus, sabemos que a soma dos outros dois ângulos em um triângulo retângulo deve ser igual a 90 graus. O lado mais longo, oposto ao ângulo reto, é chamado de hipotenusa. Um triângulo retângulo pode ser escaleno (que tem três lados de comprimentos diferentes) ou isósceles (que tem dois lados do mesmo comprimento).
A seguir, veremos a definição de um triângulo retângulo isósceles. Além disso, conheceremos suas fórmulas mais importantes e as aplicaremos para resolver alguns problemas.
Definição do triângulo retângulo isósceles
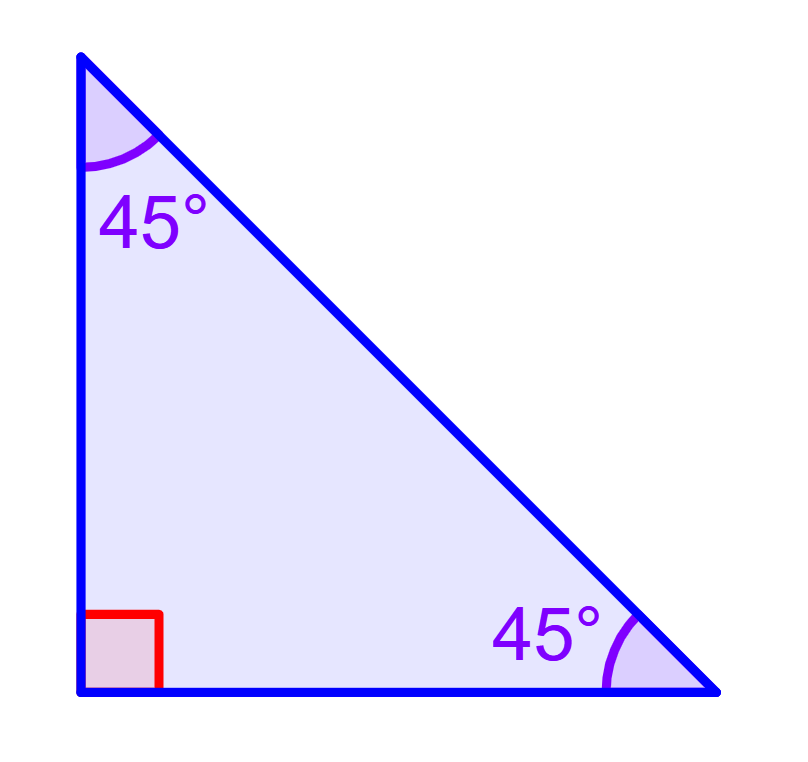
Um triângulo retângulo isósceles é um triângulo de ângulo de 90 graus que consiste em dois lados de comprimentos iguais. Como os dois lados têm comprimentos iguais, os ângulos correspondentes serão congruentes (a mesma medida).
Portanto, em um triângulo retângulo isósceles, dois lados e dois ângulos agudos são congruentes.
Por ser um triângulo retângulo, o ângulo entre os dois lados medirá 90 graus. Portanto, os lados serão perpendiculares entre si.
Fórmulas de triângulo retângulo isósceles comumente usadas
A fórmula mais importante associada aos triângulos retângulos é o teorema de Pitágoras. De acordo com este teorema, o quadrado da hipotenusa é igual à soma dos quadrados dos outros dois lados do triângulo retângulo.
No caso de um triângulo retângulo isósceles, sabemos que os outros dois lados são iguais em comprimento. Portanto, podemos encontrar a hipotenusa usando a seguinte fórmula:
| $latex {{h}^2}={{l}^2}+{{l}^2}$ $latex {{h}^2}=2{{l}^2}$ |
onde, h é o comprimento da hipotenusa e l é o comprimento dos lados.
Área de um triângulo retângulo isósceles
A área de qualquer triângulo pode ser calculada usando a fórmula $latex A = \frac{1}{2} bh$, onde b é o comprimento da base do triângulo e h é o comprimento da altura. Como em um triângulo retângulo isósceles os lados têm o mesmo comprimento, podemos usar l para representar o comprimento de cada lado e temos a fórmula:
| $latex A= \frac{1}{2}l \times l$ $latex A= \frac{1}{2}{{l}^2}$ |
onde, l é o comprimento de um dos lados congruentes do triângulo.
Perímetro de um triângulo retângulo isósceles
O perímetro é igual à soma dos comprimentos de todos os lados do triângulo. Assim, podemos calcular o perímetro de um triângulo usando a fórmula $latex p = a + b + c$, onde $latex a, ~ b, ~ c$ são os comprimentos dos lados.
Em um triângulo retângulo isósceles, sabemos que os lados têm comprimentos congruentes, então temos a seguinte fórmula:
| $latex p=h+l+l$ $latex p=h+2l$ |
onde, h é o comprimento da hipotenusa e l é o comprimento dos lados congruentes.
Exemplos de problemas de triângulo retângulo isósceles
EXEMPLO 1
- Qual é o comprimento da hipotenusa de um triângulo que tem lados congruentes de 5 m de comprimento?
Solução: Podemos usar o teorema de Pitágoras para encontrar a hipotenusa. Como temos dois lados congruentes, usamos a seguinte fórmula:
$latex {{h}^2}=2{{l}^2}$
$latex {{h}^2}=2({{5}^2})$
$latex {{h}^2}=2(25)$
$latex {{h}^2}=50$
$latex h=7,07$
O comprimento da hipotenusa é de 7,07 m.
EXEMPLO 2
- Um triângulo retângulo isósceles tem lados congruentes de 10 m de comprimento. Qual é a sua área?
Solução: Usamos a fórmula modificada da área com o valor $latex l = 10$ que é o comprimento dos lados congruentes:
$latex A= \frac{1}{2}{{l}^2}$
$latex A= \frac{1}{2}({{10}^2})$
$latex A= \frac{1}{2}(100)$
$latex A=50$
A área do triângulo é de 50 m².
EXEMPLO 3
- Qual é o perímetro de um triângulo que tem uma hipotenusa de 19,8 m e lados congruentes de comprimento 14 m?
Solução: Podemos usar a fórmula do perímetro para resolver isso. Temos dois lados congruentes, então usamos a seguinte fórmula:
$latex p=h+2l$
$latex p=19,8+2(14)$
$latex p=19,8+28$
$latex p=47,8$
O perímetro é de 47,8 m.
Exercícios de triângulo retângulo isósceles para resolver
Veja também
Você quer aprender mais sobre triângulos isósceles? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
