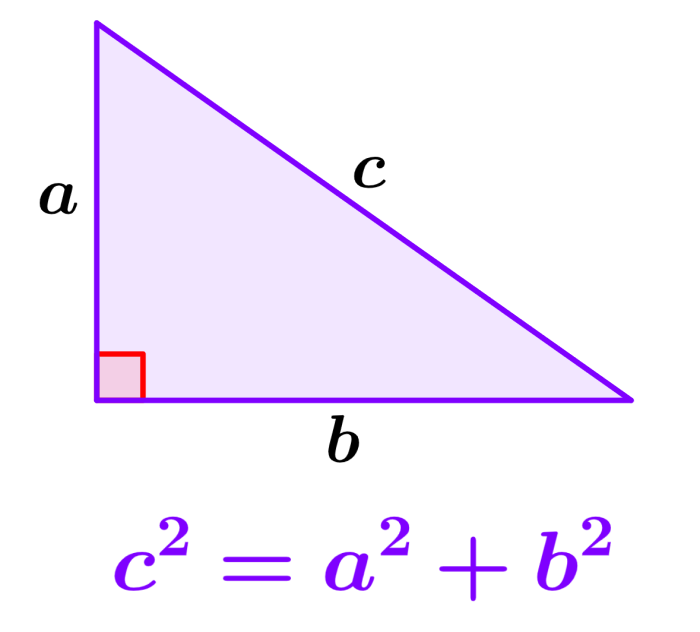O teorema de Pitágoras é talvez um dos mais importantes teoremas da matemática. Há uma variedade de provas que podem ser usadas para provar o teorema de Pitágoras. No entanto, as mais importantes são a prova de Pitágoras, a prova Euclidiana, a prova através do uso de triângulos semelhantes e a prova através do uso de álgebra.
A seguir, vamos aprender um pouco da história deste teorema. Além disso, aprenderemos como prová-lo usando vários métodos.
História do teorema de Pitágoras
Pitágoras de Samos (569-500 aC) nasceu na ilha de Samos na Grécia e viajou extensivamente pelo Egito, aprendendo matemática e outras coisas. Mais detalhes sobre como foram seus primeiros anos são desconhecidos. Pitágoras começou a ganhar reconhecimento e status ao fundar um grupo conhecido como Irmandade de Pitágoras, cujo objetivo era o estudo da matemática.
A irmandade pitagórica tinha vários aspectos de um culto, como símbolos, rituais e orações. Além disso, Pitágoras acreditava que “o número governa o universo”, e membros do grupo pitagórico davam valores numéricos a muitos objetos e ideias. Esses valores numéricos, por sua vez, eram dotados de qualidades místicas e espirituais.
Uma lenda conta que quando Pitágoras terminou seu famoso teorema, ele sacrificou 100 bois. Embora este teorema seja atribuído a Pitágoras, não é possível saber com certeza se ele foi realmente o verdadeiro autor. O grupo da Irmandade Pitagórica trabalhou em muitas provas geométricas, mas é difícil saber quem provou o quê, pois o grupo sempre tentou manter suas descobertas em segredo.
Infelizmente, esse voto de sigilo impediu que uma importante ideia matemática fosse conhecida publicamente. A Irmandade Pitagórica descobriu números irracionais. Quando consideramos um triângulo retângulo isósceles com catetos de medida 1, a hipotenusa medirá a raiz quadrada de 2.
No entanto, sabemos que esse número não pode ser expresso como um comprimento que pode ser medido com partes fracionárias, e isso perturbou profundamente os pitagóricos, que acreditavam que «Tudo é número».
Prova de Pitágoras
Vamos começar com o seguinte triângulo:
Este triângulo tem catetos com comprimentos a e b e uma hipotenusa com comprimento c. Agora, usamos quatro desses triângulos para formar um quadrado com lados de comprimento $latex a+b$ conforme mostrado na imagem a seguir:
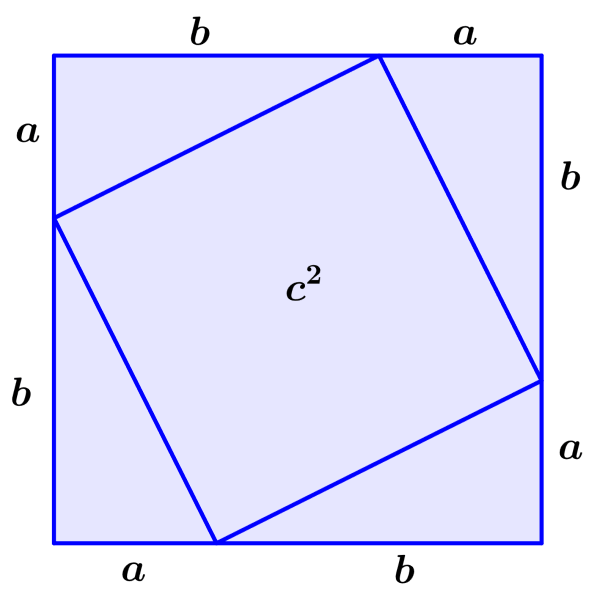
Como a hipotenusa desses triângulos é igual a c, os lados do quadrado interno também são iguais a c e sua área é igual a $latex {{c}^2}$.
Agora, também podemos organizar os triângulos da seguinte maneira e formar dois quadrados que tenham áreas $latex {{a}^2}$ e $latex {{b}^2}$.
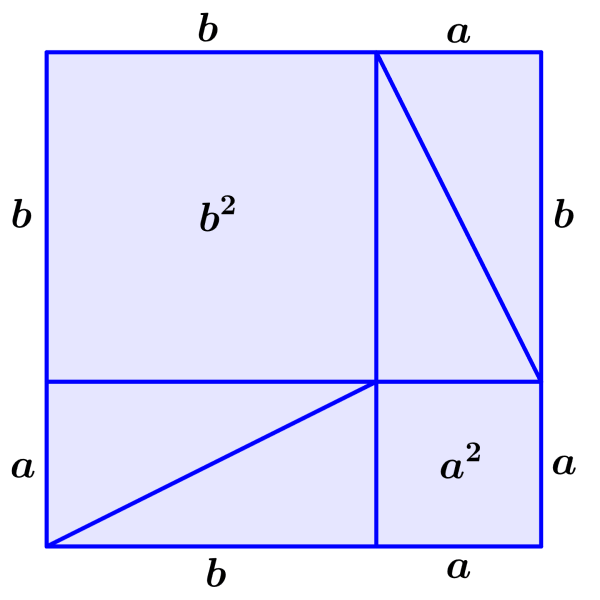
Então sabemos que a área dos dois quadrados grandes é a mesma nos dois casos. Além disso, também sabemos que os quatro triângulos são os mesmos em ambos os casos. Isso significa que a área dos quadrados $latex {{a}^2}$ e $latex {{b}^2}$ é igual à área do quadrado $latex {{c}^2} $. Ou seja, temos:
$latex {{a}^2}+{{b}^2}={{c}^2}$
A prova de Euclides
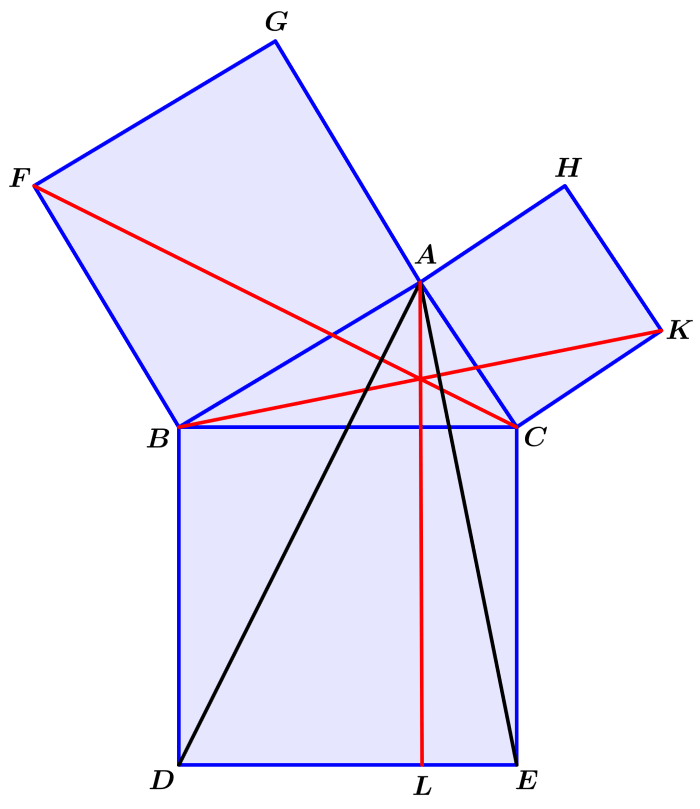
No diagrama abaixo, o triângulo ABC é um triângulo retângulo com um ângulo reto em A.
De acordo com o teorema de Pitágoras, o quadrado do lado BC é igual à soma dos quadrados dos lados BA e AC.
Traçamos a reta AL que vai de A e é paralela aos lados BD e CE. Além disso, também traçamos as linhas AD e FC.
Como o ângulo BAC e o ângulo BAG são ângulos retos, as linhas CA e AG formam uma linha reta. Pela mesma razão, as linhas BA e AH também formam uma linha reta.
Agora, como os ângulos DBC e FBA são ângulos retos, podemos adicionar o ângulo ABC um ao outro e isso significa que os ângulos DBA e FBC são iguais.
Além disso, como o segmento DB é igual a BC e o segmento FB é igual a BA, os lados AB e BD são iguais aos lados FB e BC, respectivamente. Além disso, o ângulo ABD é igual ao ângulo FBC, então a base AD é igual à base FC e o triângulo ABD é igual ao triângulo FBC.
Notamos que o paralelogramo BL é o dobro do triângulo ABD, pois eles compartilham a mesma base BD e estão nos mesmos segmentos paralelos BD e AL, o que significa que a altura do triângulo é igual à altura do paralelogramo. Além disso, o quadrado GB é o dobro do triângulo FBC, pois eles têm a mesma base FB e estão nos mesmos segmentos paralelos FB e CG.
Portanto, o paralelogramo BL é igual ao quadrado GB.
Seguindo este mesmo processo, podemos formar os segmentos AE e BK para mostrar que o paralelogramo CL é igual ao quadrado HC. Isso significa que o quadrado BDEC é igual à soma dos quadrados GB e HC.
Considerando que o quadrado BDEC é descrito pelo lado BC e os quadrados GB e HC são descritos pelos lados BA e AC respectivamente, temos que o quadrado do lado BC (hipotenusa) é igual à soma dos quadrados de BA e AC (catetos).
Prova usando triângulos semelhantes
Dois triângulos são semelhantes quando seus ângulos correspondentes compartilham as mesmas medidas e seus lados correspondentes têm as mesmas proporções.
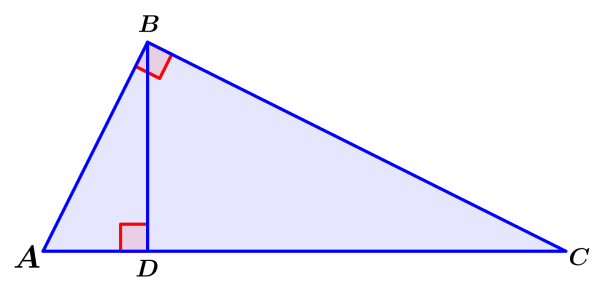
Usamos os seguintes triângulos semelhantes:
O triângulo ABD e o triângulo ABC têm as seguintes características:
- ∠A = ∠A esses ângulos são comuns
- ∠ADB = ∠ABC ambos os ângulos são retos
Vemos que esses triângulos compartilham dois ângulos. Além disso, sabemos que todos os triângulos têm uma soma interna dos ângulos igual a 180°, o que significa que se dois triângulos têm dois ângulos com as mesmas medidas, o terceiro ângulo também deve ter as mesmas medidas.
Assim, podemos deduzir que os triângulos ABD e ABC têm os mesmos ângulos. Isso significa que esses triângulos são semelhantes. Da mesma forma, podemos provar que os triângulos BCD e ACB são semelhantes.
Como os triângulos ABD e ACB são semelhantes, temos as proporções $latex \frac{AD}{AB}=\frac{AB}{AC}$. Podemos reescrever isso e dizer que $latex AD\times AC={{AB}^2}$.
Da mesma forma, os triângulos BCD e ACB são semelhantes, então temos as proporções $latex \frac{CD}{BC}=\frac{BC}{AC}$. Podemos reescrever isso e dizer que $latex CD\times AC={{BC}^2}$.
Usando essas duas equações, podemos concluir que $latex {{AC}^2}={{AB}^2}+{{BC}^2}$. Provamos o teorema de Pitágoras.
Prova usando álgebra
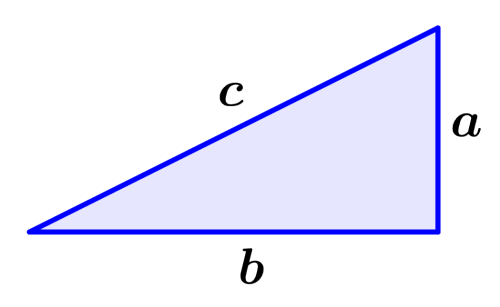
Para provar o Teorema de Pitágoras usando álgebra, precisamos usar quatro cópias de um triângulo retângulo com lados a e b dispostos em torno de um quadrado central com lados de comprimento c, conforme mostrado no diagrama abaixo.
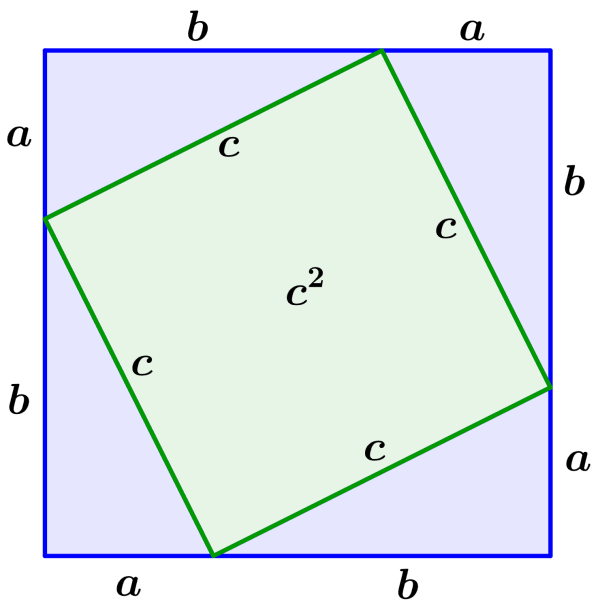
Neste diagrama, b é a base dos triângulos, a é a altura e c é a hipotenusa. Ao organizar os triângulos como mostrado no diagrama, formamos um grande quadrado com lados de comprimento $latex a+b$.
A área do quadrado central formado pelas hipotenusas dos triângulos é igual a $latex {{c}^2}$. Além disso, a área do quadrado com lados $latex a+b$ é igual à área dos quatro triângulos mais a área do quadrado central com lados c. Ou seja, temos:
$latex {{(a+b)}^2}=4(\frac{1}{2}\times a\times b)+{{c}^2}$
$latex {{a}^2}+{{b}^2}+2ab=2ab+{{c}^2}$
$latex {{a}^2}+{{b}^2}=c^2$
Veja também
Interessado em aprender mais sobre o Teorema de Pitágoras? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
