O teorema de Pitágoras tem um grande número de aplicações em diversas áreas. Por exemplo, em arquitetura e construção, o teorema de Pitágoras pode ser usado para encontrar comprimentos de vários objetos que formam ângulos retos. Em topografia, a inclinação de colinas ou montanhas é calculada usando este teorema.
Além disso, podemos usar o teorema de Pitágoras na navegação para encontrar a distância mais curta entre dois pontos e o ângulo a seguir.
Arquitetura e construção
O teorema de Pitágoras nos permite calcular o comprimento da diagonal que liga duas retas que formam um ângulo reto. Esta aplicação é frequentemente utilizada em arquitetura para encontrar os comprimentos de diferentes objetos a serem utilizados na construção.
Além disso, isso também é útil em carpintaria e outros projetos de construção de objetos físicos que exigem medições precisas. Por exemplo, um arquiteto pode projetar um telhado inclinado.
Conhecendo a altura do telhado, bem como seu comprimento, você pode determinar facilmente o comprimento da inclinação do telhado usando o teorema de Pitágoras.
Topografia
O levantamento topográfico é o processo usado pelos cartógrafos para calcular as distâncias e alturas de diferentes pontos para produzir mapas altamente precisos. Como o terreno geralmente é irregular, os cartógrafos precisam usar métodos sistemáticos para encontrar medições de distância.
Com o teorema de Pitágoras, é possível calcular a inclinação de montanhas e colinas. Um agrimensor usa um telescópio para olhar para uma haste de medição que é colocada a uma distância fixa, de modo que o ponto de vista do telescópio e a haste de medição formem um ângulo reto.
Como o agrimensor conhece a distância exata até a localização da barra e sua altura, ele pode usar o teorema de Pitágoras para calcular o comprimento da inclinação e a medida de sua inclinação.
Navegação
O teorema de Pitágoras pode ser usado para navegar mais facilmente no plano bidimensional. Especificamente, podemos usar o teorema para encontrar a distância mais curta entre dois pontos.
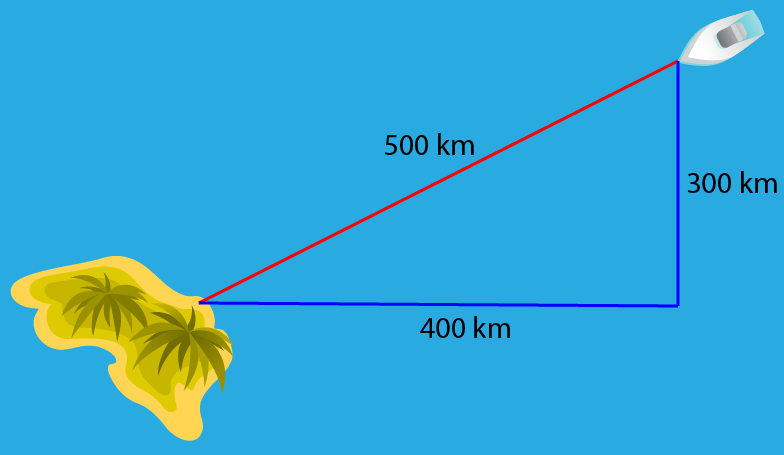
Por exemplo, se estivéssemos navegando no oceano e quiséssemos nos mudar para uma ilha que fica a 300 quilômetros ao sul e 400 quilômetros a oeste, podemos calcular a distância mais curta entre os pontos e até encontrar o ângulo no sudoeste que temos de continuar para chegar à ilha.
As distâncias sul e oeste serão os catetos de um triângulo retângulo, e a distância mais curta é a hipotenusa do triângulo.
O mesmo princípio pode ser usado para navegação aérea. Por exemplo, se o avião estiver próximo ao aeroporto de pouso, é possível usar sua altura acima do solo e sua distância horizontal do aeroporto para encontrar o local correto onde você precisa começar a descer.
Gráfico de ângulo quadrado
O teorema de Pitágoras pode ser usado na construção de casas ou edifícios para garantir que as construções sejam quadradas. Isso porque um triângulo que tem lados que correspondem ao teorema de Pitágoras, como um triângulo que mede 3 metros por 4 metros por 5 metros, sempre será um triângulo retângulo.
Assim, ao trabalhar na fundação ou construir um canto quadrado entre duas paredes, os pedreiros podem formar um triângulo com três cordas correspondentes a esses comprimentos.
Desde que as cordas tenham sido medidas corretamente, o canto oposto à hipotenusa do triângulo corresponde a um ângulo reto, então os pedreiros podem seguir essas linhas para construir um canto quadrado.
Veja também
Quer saber mais sobre o Teorema de Pitágoras? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
