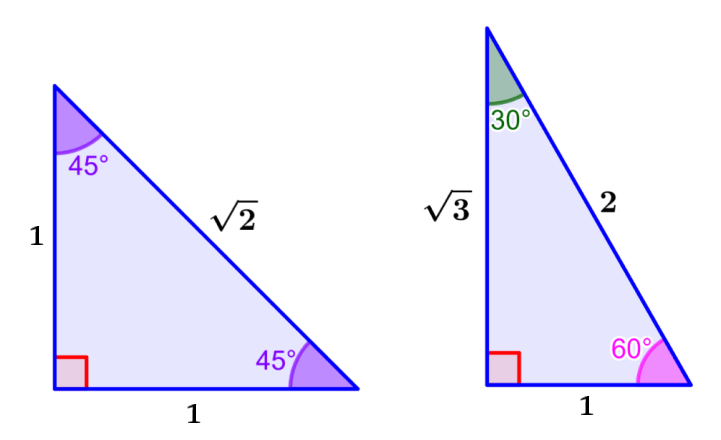
Ângulos notáveis são ângulos que possuem valores que são comuns em exercícios de trigonometria e na vida cotidiana em geral. Geralmente, os ângulos notáveis são os ângulos de 30°, 45° e 60°. Esses ângulos têm razões trigonométricas fáceis de lembrar.
A seguir, conheceremos as razões trigonométricas dos ângulos notáveis de 30°, 45° e 60°. Além disso, aprenderemos como derivar essas razões trigonométricas.
Razões trigonométricas de 45°
Para encontrar as razões trigonométricas de um ângulo de 45°, podemos considerar o seguinte triângulo retângulo isósceles:
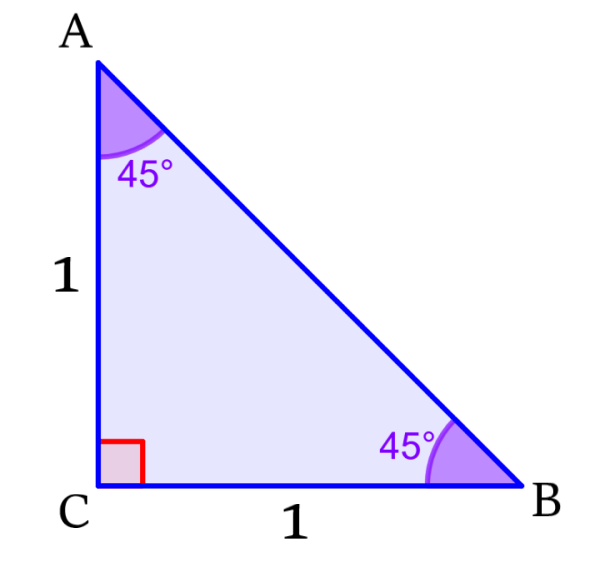
Este triângulo tem dois ângulos com as mesmas medidas, então ambos os seus catetos têm o mesmo comprimento de 1 unidade.
Podemos usar o teorema de Pitágoras para encontrar o comprimento da hipotenusa:
$latex {{AB}^2}={{BC}^2}+{{AC}^2}$
$latex {{AB}^2}={{1}^2}+{{1}^2}$
$latex {{AB}^2}=2$
$latex AB=\sqrt{2}$
Agora, podemos usar o mesmo triângulo para obter os valores das razões trigonométricas, seno, cosseno e tangente:
Usando a definição de seno (lado oposto sobre a hipotenusa), temos:
$$\sin(45^{\circ})=\frac{AC}{AB}=\frac{1}{\sqrt{2}}$$
Usando a definição de cosseno (lado adjacente sobre a hipotenusa), temos:
$$\cos(45^{\circ})=\frac{BC}{AB}=\frac{1}{\sqrt{2}}$$
Usando a definição da tangente (lado oposto sobre o lado adjacente), temos:
$$\tan(45^{\circ})=\frac{AC}{BC}=1$$
Em resumo, temos o seguinte:
| $$\sin(45^{\circ})=\frac{1}{\sqrt{2}}$$ $$\cos(45^{\circ})=\frac{1}{\sqrt{2}}$$ $$\tan(45^{\circ})=1$$ |
Razões trigonométricas de 30°
Para encontrar as razões trigonométricas do ângulo de 30°, vamos usar um triângulo equilátero com lados de 2 unidades.
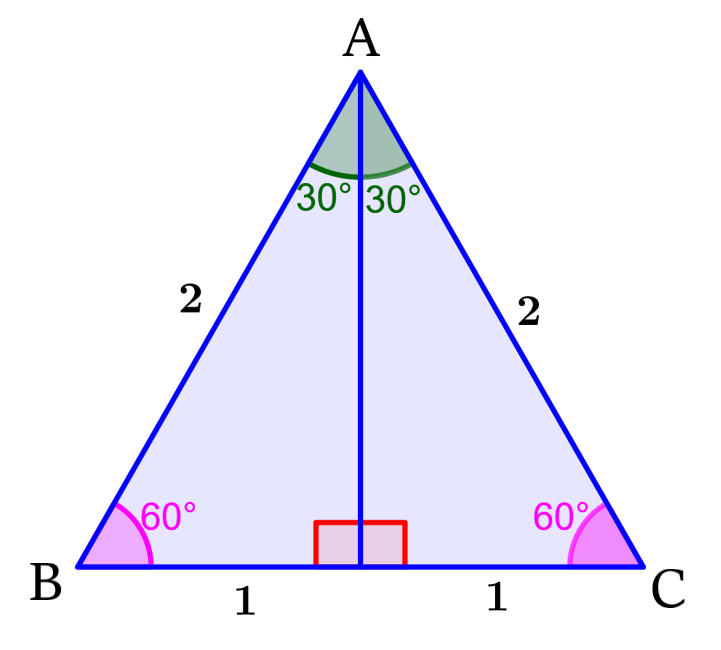
D é o ponto onde o segmento perpendicular de A encontra a base. O segmento AD divide o triângulo equilátero em dois triângulos iguais que têm os ângulos 30°, 60° e 90°.
Podemos encontrar o comprimento do segmento AD usando o teorema de Pitágoras:
$latex {{AD}^2}+{{BD}^2}={{AB}^2}$
$latex {{AD}^2}+{{1}^2}={{2}^2}$
$latex {{AD}^2}+1=4$
$latex {{AD}^2}=3$
$latex AD=\sqrt{3}$
Usando a definição de seno (lado oposto sobre a hipotenusa), temos:
$$\sin(30^{\circ})=\frac{BD}{AB}=\frac{1}{2}$$
Usando a definição de cosseno (lado adjacente sobre a hipotenusa), temos:
$$\cos(30^{\circ})=\frac{AD}{AB}=\frac{\sqrt{3}}{2}$$
Usando a definição da tangente (lado oposto sobre o lado adjacente), temos:
$$\tan(30^{\circ})=\frac{BD}{AD}=\frac{1}{\sqrt{3}}$$
Em resumo, temos o seguinte:
| $$\sin(30^{\circ})=\frac{1}{2}$$ $$\cos(30^{\circ})=\frac{\sqrt{3}}{2}$$ $$\tan(30^{\circ})=\frac{1}{\sqrt{3}}$$ |
Razões trigonométricas de 60°
Podemos encontrar as razões trigonométricas do ângulo de 60° usando o mesmo triângulo que usamos para encontrar as razões trigonométricas de 30°.

Então, usamos os comprimentos $latex AB=2$, $latex BD=1$ e $latex AD=\sqrt{3}$ com as funções trigonométricas seno, cosseno e tangente.
Usando a definição de seno (lado oposto sobre a hipotenusa), temos:
$$\sin(60^{\circ})=\frac{AD}{AB}=\frac{\sqrt{3}}{2}$$
Usando a definição de cosseno (lado adjacente sobre a hipotenusa), temos:
$$\cos(60^{\circ})=\frac{BD}{AB}=\frac{1}{2}$$
Usando a definição da tangente (lado oposto sobre o lado adjacente), temos:
$$\tan(60^{\circ})=\frac{AD}{BD}=\sqrt{3}$$
Em resumo, temos o seguinte:
| $$\sin(60^{\circ})=\frac{\sqrt{3}}{2}$$ $$\cos(60^{\circ})=\frac{1}{2}$$ $$\tan(60^{\circ})=\sqrt{3}$$ |
Tabela das razões trigonométricas de ângulos notáveis
As razões trigonométricas dos ângulos 30°, 45° e 60° estão resumidas na tabela a seguir:
| Razão | θ = 30° | θ = 30° | θ = 30° |
| sin θ | $latex \frac{1}{2}$ | $latex \frac{1}{\sqrt{2}}$ | $latex \frac{\sqrt{3}}{2}$ |
| cos θ | $latex \frac{\sqrt{3}}{2}$ | $latex \frac{1}{\sqrt{2}}$ | $latex \frac{1}{2}$ |
| tan θ | $latex \frac{1}{\sqrt{3}}$ | 1 | $latex \sqrt{3}$ |
É uma boa ideia memorizar essas razões trigonométricas, pois vários problemas encontrados em trigonometria usam os ângulos de 30°, 45° e 60°.
Veja também
Interessado em aprender mais sobre ângulos e triângulos especiais? Veja estas páginas: