Um triângulo retângulo é uma das figuras mais importantes da geometria e forma a base da trigonometria. Esses triângulos são caracterizados por terem um ângulo de 90 graus. Por causa disso, os triângulos retângulos geram o teorema mais importante que é o teorema de Pitágoras.
A seguir, veremos uma definição de triângulos retângulos e conheceremos suas características mais importantes. Além disso, aprenderemos suas fórmulas mais importantes e as aplicaremos para resolver alguns exercícios.
GEOMETRIA
Relevante para…
Aprender sobre as características dos triângulos retângulos.
GEOMETRIA
Relevante para…
Aprender sobre as características dos triângulos retângulos.
Definição de um triângulo retângulo
Um triângulo retângulo é um triângulo que tem um ângulo de 90 graus. Esses triângulos têm três lados, “base”, “hipotenusa” e “altura”, onde o ângulo entre a base e a altura é de 90 graus. Este triângulo é uma figura muito importante na matemática porque dá origem ao teorema de Pitágoras.
Lembre-se de que o teorema de Pitágoras nos diz que o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos outros lados.
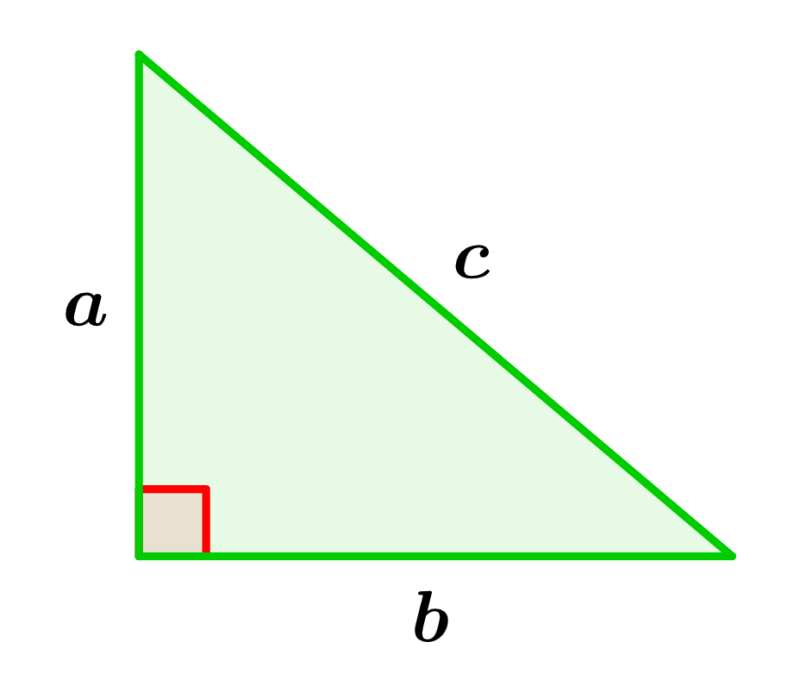
Por exemplo, no triângulo retângulo a seguir, a hipotenusa é “c“, pois é o lado oposto ao ângulo de 90 graus e os outros lados têm comprimentos a e b
Características de triângulos retângulos
A seguir estão as características mais importantes dos triângulos retângulos:
- Um ângulo do triângulo é sempre 90°, ou seja, um ângulo reto.
- O lado oposto do ângulo reto é a hipotenusa.
- A hipotenusa é sempre o lado mais longo.
- A soma dos outros ângulos internos é igual a 90°.
- Os outros dois lados adjacentes ao ângulo reto são chamados de base e perpendicular.
- Se desenharmos um círculo que passa pelos três vértices, o raio desse círculo é igual a metade da hipotenusa.
- Se um dos ângulos é de 90° e os outros dois ângulos medem 45° cada, o triângulo é denominado triângulo retângulo isósceles, em que os lados adjacentes ao ângulo de 90° são iguais.
Fórmulas importantes para triângulos retângulos
As três fórmulas mais importantes para triângulos retângulos são a fórmula da área, a fórmula do perímetro e o teorema de Pitágoras.
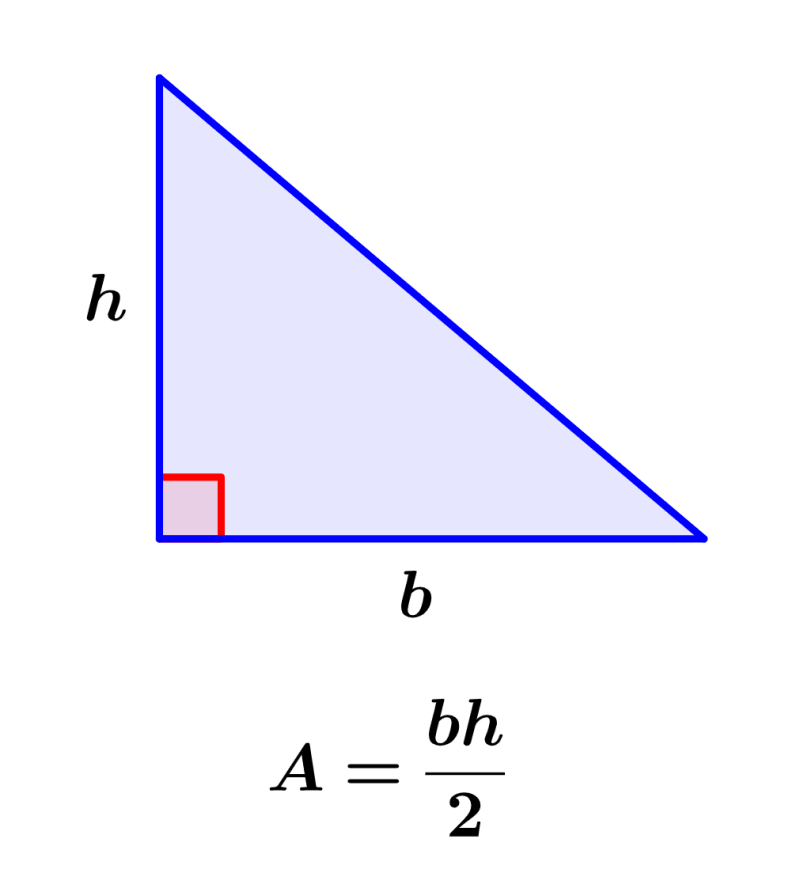
Área de um triângulo retângulo
A área de um triângulo retângulo é calculada usando o comprimento da base e o comprimento da altura:
| $latex A= \frac{b \times h}{2}$ |
onde, b é o comprimento da base e h é o comprimento da altura.
Perímetro de um triângulo retângulo
O perímetro de um triângulo retângulo é calculado adicionando os comprimentos de todos os lados:
| $latex p=a+b+c$ |
onde, $latex a,~b,~c$ são os comprimentos dos lados do triângulo.
Teorema de Pitágoras
O teorema de Pitágoras nos permite encontrar o comprimento da hipotenusa do triângulo se conhecermos os comprimentos dos outros dois lados:
| $latex {{c}^2}={{a}^2}+{{b}^2}$ |
onde, $latex a,~b$ são os comprimentos dos lados e c é o comprimento da hipotenusa.
Exemplos de problemas de triângulo retângulo
EXEMPLO 1
- Qual é a área de um triângulo com 12 m de altura e 14 m de base?
Solução: Temos $latex b=14$ e $latex h=12$. Então, usamos a fórmula de área com esses valores:
$latex A= \frac{b \times h}{2}$
$latex A= \frac{14 \times 12}{2}$
$latex A= \frac{168}{2}$
$latex A=84$
A área do triângulo é de 84 m².
EXEMPLO 2
- Qual é o perímetro de um triângulo que tem lados de 6 m, 8 m e 10 m de comprimento?
Solução: Temos os comprimentos $latex a = 6$, $latex b = 8$ e $latex c = 10$. Então, usamos a fórmula do perímetro com esses valores:
$latex p= a+b+c$
$latex p= 6+8+10$
$latex p=24$
O perímetro do triângulo é de 24 m.
EXEMPLO 3
- Qual é o comprimento da hipotenusa de um triângulo retângulo que tem lados de 5 m e 12 m?
Solução: Temos os comprimentos $latex a = 5$ e $latex b = 12$. Portanto, usamos o teorema de Pitágoras com estes valores:
$latex {{c}^2}= {{a}^2}+{{b}^2}$
$latex {{c}^2}= {{5}^2}+{{12}^2}$
$latex {{c}^2}= 25+144$
$latex {{c}^2}=169$
$latex c=13$
O comprimento da hipotenusa é de 13 m.
Veja também
Você quer aprender mais sobre triângulos retângulos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
