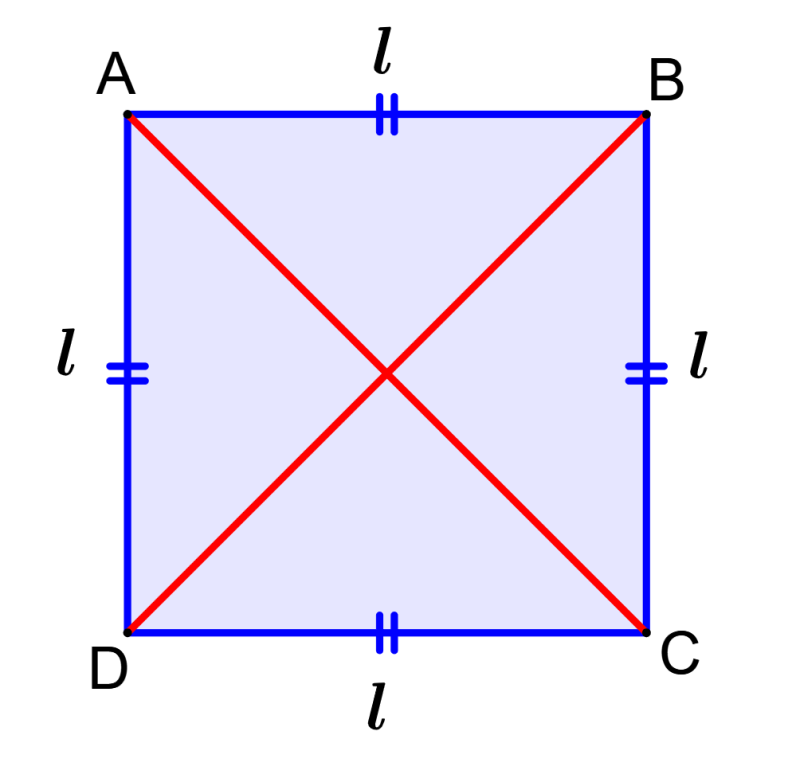
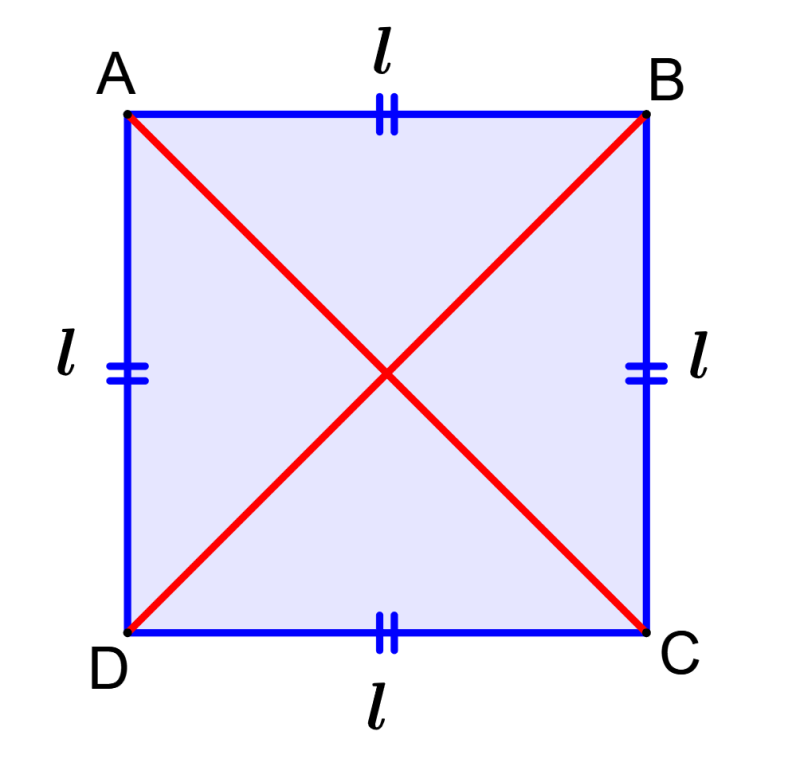
Um quadrado é uma figura bidimensional com quatro lados iguais, em que seus quatro ângulos medem 90 graus. As propriedades dos quadrados são bastante semelhantes às de um retângulo, mas a diferença entre as duas é que, em um retângulo, apenas seus lados opostos são iguais. As outras propriedades do quadrado, como área e perímetro, também diferem daquelas do retângulo.
A seguir, veremos as propriedades fundamentais dos quadrados. Além disso, veremos alguns exemplos dessas propriedades.
Propriedades fundamentais de quadrados
As propriedades fundamentais dos quadrados são as seguintes:
- Os quatro ângulos internos de um quadrado são iguais a 90°.
- Todos os quatro lados de um quadrado são congruentes (o comprimento é o mesmo).
- Os lados opostos do quadrado são paralelos um ao outro.
- As diagonais se dividem em 90°, ou seja, são perpendiculares.
- As duas diagonais são iguais (têm o mesmo comprimento).
- O quadrado possui quatro vértices e quatro lados.
- A diagonal do quadrado o divide em dois triângulos isósceles semelhantes.
- O comprimento das diagonais é maior do que o comprimento dos lados do quadrado.
- As diagonais do quadrado são os diâmetros da circunferência do quadrado.
- Um quadrado é um equilátero com quatro lados iguais e quatro ângulos internos iguais.
- Um quadrado é um losango com quatro ângulos iguais (cada ângulo tem 90°).
- Um quadrado é um retângulo, no qual seus dois lados adjacentes são iguais.
- Um quadrado é um paralelogramo com os quatro ângulos internos iguais a 90° e os lados adjacentes iguais em comprimento.
Fórmulas importantes para quadrados
A seguir estão algumas fórmulas importantes relacionadas com quadrados:
Área de um quadrado: A=l², onde l é o comprimento de cada lado do quadrado:
| Área do quadrado = (lado)²=l² |
Perímetro de um quadrado: p=comprimento total de todos os lados do quadrado= 4l, onde l é o comprimento de cada lado do quadrado:
| Perímetro = 4 × lado=4l |
Diagonal de um quadrado: Cada uma das diagonais divide o quadrado em dois triângulos retângulos iguais, onde a diagonal é a hipotenusa dos triângulos.
Podemos aplicar o teorema de Pitágoras para encontrar o comprimento da hipotenusa:
$latex {{d}^2}={{lado}^2}+{{lado}^2}$
Sabemos que um quadrado tem todos os seus lados iguais, então temos:
$latex {{d}^2}=2{{lado}^2}$
$latex d=\sqrt{2}~l$
Então,
| Diagonal =$latex \sqrt{2}~lado=\sqrt{2}~l$ |
Exemplos de problemas com quadrados
A seguir estão alguns exemplos de problemas com quadrados resolvidos.
EXEMPLO 1
- Qual é o perímetro de um quadrado com lados de 13 m de comprimento?
Solução: Sabemos que a fórmula para o perímetro de um quadrado é 4 l, onde l é o comprimento dos lados do quadrado. Então, usando $latex l = 13$, temos:
$latex p=4l$
$latex p=4(13)$
$latex p=52$
O perímetro do quadrado é de 52 m.
EXEMPLO 2
- Se um quadrado tem lados com 15 cm de comprimento, qual é a sua área?
Solução: Um quadrado tem todos os seus lados iguais e sua área pode ser calculada quadrando um de seus lados. Então, usando o comprimento dado, temos:
$latex A={{l}^2}$
$latex A={{15}^2}$
$latex A=225$
A área do quadrado é de 225 cm².
EXEMPLO 3
- Qual é o comprimento da diagonal de um quadrado com lados de 8 m?
Solução: A diagonal do quadrado é calculada usando o teorema de Pitágoras. Então, para simplificar, obtemos a seguinte fórmula, na qual usamos $latex l=8$:
$latex d=\sqrt{2}~l$
$latex d=\sqrt{2}~(8)$
$latex d=8\sqrt{2}$
A diagonal do quadrado tem um comprimento de $latex 8\sqrt{2}$ m.
Veja também
Você quer aprender mais sobre quadrados? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
