O perímetro de um círculo representa o comprimento do contorno do círculo, ou seja, o perímetro é igual à circunferência. Por outro lado, a área é uma medida da região ocupada pelo círculo no plano bidimensional. O perímetro de um círculo pode ser calculado usando a fórmula C = 2πr e a área pode ser calculada usando a fórmula A = πr², onde r é o raio do círculo.
A seguir, aprenderemos detalhadamente sobre o perímetro e a área de um círculo. Conheceremos suas fórmulas e as aplicaremos para resolver alguns exercícios práticos.
GEOMETRIA
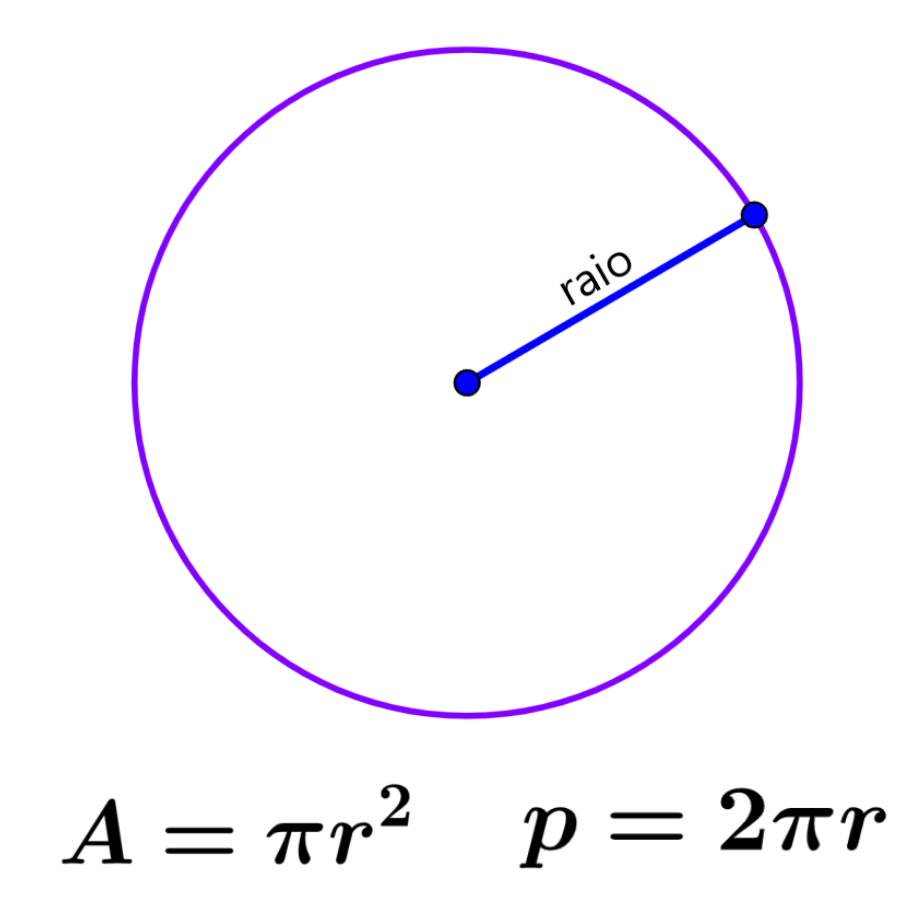
Relevante para…
Aprender sobre o perímetro e a área de um círculo com exercícios.
GEOMETRIA
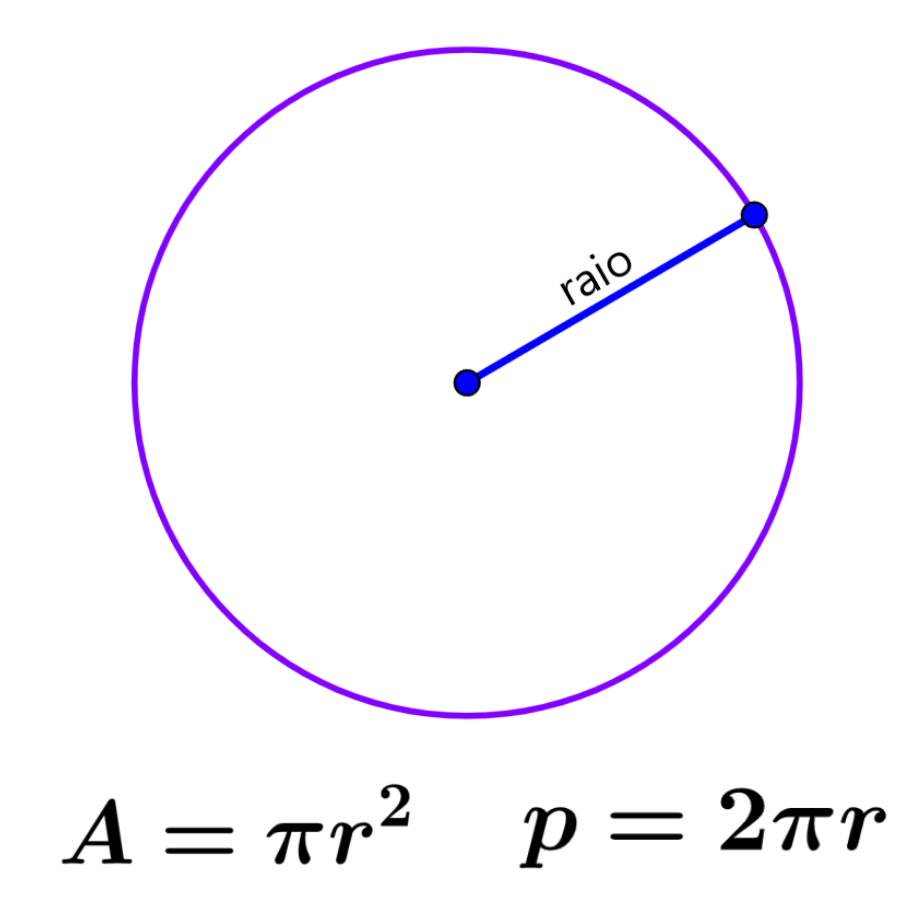
Relevante para…
Aprender sobre o perímetro e a área de um círculo com exercícios.
Como calcular o perímetro de um círculo?
Podemos calcular o perímetro de um círculo, também conhecido como circunferência, multiplicando o comprimento de seu diâmetro pela constante pi. Assim, temos a seguinte fórmula:
| $latex C=\pi d$ |
Aqui, d é o comprimento do diâmetro e π é uma constante matemática com um valor de aproximadamente 3,141592…
Para entender a definição de π, podemos considerar o seguinte círculo:
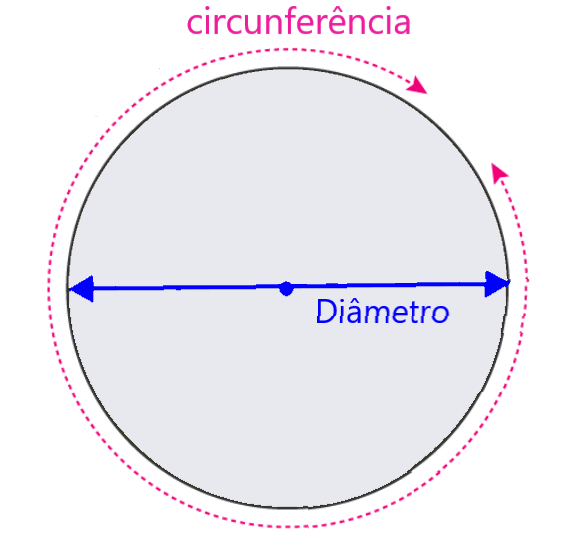
Como já mencionamos, o perímetro é igual à circunferência, pois é o comprimento do contorno do círculo. Além disso, vemos que o diâmetro é a distância que cruza o círculo e passa pelo centro. A constante π é a razão entre a circunferência e o diâmetro.
Assim, a definição de π é a seguinte:
$latex \frac{C}{d}=\pi$
Reorganizando a fórmula, temos a fórmula para a circunferência ou perímetro do círculo:
$latex C=\pi d$
Calcular o perímetro de um círculo com o raio
Para calcular o perímetro de um círculo usando o raio, tomamos o diâmetro igual a 2r. Assim, podemos reescrever a fórmula do perímetro da seguinte forma:
| $latex C=2\pi r$ |
Como calcular a área de um círculo?
Para calcular a área de um círculo, podemos multiplicar π pelo raio do círculo ao quadrado. Assim, temos a seguinte fórmula:
| $latex A=πr^2$ |
Lembre-se que o raio de um círculo é o segmento que une o centro do círculo com a circunferência. O seguinte é um círculo com raio r:
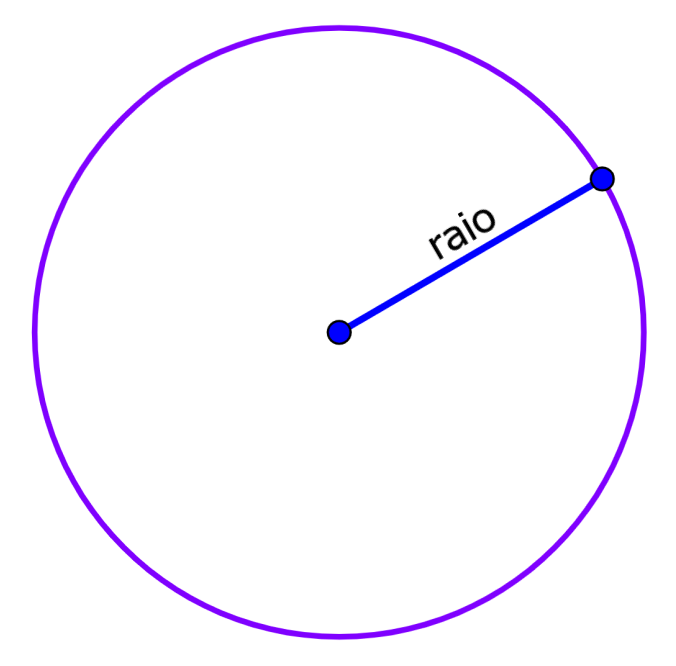
Prova da fórmula para a área de um círculo
A fórmula para a área de um círculo pode ser provada usando várias técnicas. Algumas das técnicas mais avançadas incluem o uso do Cálculo. No entanto, aqui vamos simplificar um pouco a demonstração usando o seguinte diagrama:
Se cortarmos o círculo em vários setores, podemos reorganizar os setores e formar uma figura em forma de paralelogramo. Se fizermos cortes pequenos o suficiente, eventualmente formaremos um paralelogramo.
Se o número de setores cortados do círculo for aumentado, o paralelogramo acabará se parecendo com um retângulo com base igual a πr e altura igual a r.
Como a área de um retângulo é igual ao comprimento de sua base multiplicado por sua altura, temos:
$latex A=\pi r\times r$
$latex A=\pi {{r}^2}$
Calcular a área de um círculo usando o diâmetro
Para calcular a área de um círculo usando o diâmetro, lembramos que o diâmetro é igual a 2r. Equivalentemente, podemos escrever $latex r=\frac{d}{2}$. Então, usamos essa equivalência na fórmula para a área de um círculo:
$latex A=\pi {{r}^2}$
$latex A=\pi {{(\frac{d}{2})}^2}$
| $latex A=\pi (\frac{{{d}^2}}{4})$ |
onde, d é o comprimento do diâmetro
Perímetro e área de um círculo – Exercícios resolvidos
As fórmulas para o perímetro e a área de um círculo são usadas para resolver os seguintes exercícios. Tente resolver os exercícios antes de olhar para a solução.
EXERCÍCIO 1
Encontre o perímetro de um círculo que tem um diâmetro de 6 metros.
Solução
Usamos o valor $latex d=6$ na fórmula de perímetro com diâmetro:
$latex C=\pi d$
$latex C=\pi (6)$
$latex C=18,8$
O perímetro do círculo é igual a 18,8 m.
EXERCÍCIO 2
Se um círculo tem um raio de 5 cm, qual é a sua área?
Solução
Vamos usar a fórmula da área com raio com o valor $latex r=5$. Então temos:
$latex A=\pi {{r}^2}$
$latex A=\pi {{(5)}^2}$
$latex A=\pi (25)$
$latex A=78,5$
A área do círculo é de 78,5 cm².
EXERCÍCIO 3
Encontre o perímetro de um círculo que tem um diâmetro de 15 cm.
Solução
Aplicamos a fórmula para o perímetro de um círculo com o valor $latex d=15$:
$latex C=\pi d$
$latex C=\pi (15)$
$latex C=47,1$
O perímetro é igual a 47,1 cm.
EXERCÍCIO 4
Encontre a área de um círculo que tem um raio de 12 mm.
Solução
Usando a fórmula da área de um círculo com o valor $latex r=12$, temos:
$latex A=\pi {{r}^2}$
$latex A=\pi {{(12)}^2}$
$latex A=\pi (144)$
$latex A=452,4$
A área do círculo é 452,4 mm².
EXERCÍCIO 5
Encontre o comprimento do perímetro de um círculo que tem um raio de 8 m.
Solução
Aqui, temos o comprimento do raio em vez do diâmetro, então usamos o valor $latex r=8$ na seguinte fórmula:
$latex C=2\pi r$
$latex C=2\pi (8)$
$latex C=50,3$
O perímetro é igual a 50,3 m.
EXERCÍCIO 6
Encontre a área de um círculo que tem um diâmetro de 10 m.
Solução
Usamos a fórmula da área de um círculo em função do diâmetro com o valor $latex d=10$:
$latex A=\pi(\frac{{{d}^2}}{4})$
$latex A=\pi(\frac{{{(10)}^2}}{4})$
$latex A=\pi(\frac{100}{4})$
$latex A=\pi(25)$
$latex A=78,5$
A área do círculo é de 78,5 m².
EXERCÍCIO 7
Encontre o perímetro de um círculo que tem um raio de 13 mm.
Solução
Usamos o valor $latex r=13$ na fórmula para o perímetro de um círculo. Então temos:
$latex C=2\pi r$
$latex C=2\pi (13)$
$latex C=81,7$
O perímetro é igual a 81,7 mm.
EXERCÍCIO 8
Qual é a área que um círculo tem um diâmetro de 20 cm?
Solução
Vamos usar a fórmula para a área de um círculo em termos de diâmetro. Então, substituímos o valor $latex d=20$:
$latex A=\pi(\frac{{{d}^2}}{4})$
$latex A=\pi(\frac{{{(20)}^2}}{4})$
$latex A=\pi(\frac{400}{4})$
$latex A=\pi(100)$
$latex A=314,16$
A área do círculo é 314,16 cm².
EXERCÍCIO 9
Qual é o diâmetro de um círculo que tem um perímetro de 100 mm?
Solução
Neste exercício, conhecemos o perímetro do círculo e vamos encontrar o diâmetro, então usamos o valor $latex C=100$ na fórmula e resolvemos para d:
$latex C=\pi d$
$latex 100=\pi d$
$latex d=\frac{100}{\pi}$
$latex d=31,8$
O comprimento do diâmetro é igual a 31,8 mm.
EXERCÍCIO 10
Encontre o comprimento do raio de um círculo que tem uma área de 150 cm².
Solução
Neste exercício, conhecemos a área e vamos encontrar o comprimento do raio. Então, usamos o valor $latex A=150$ na fórmula da área e resolvemos para r:
$latex A=\pi {{r}^2}$
$latex 150=\pi {{r}^2}$
$latex {{r}^2}=\frac{150}{\pi}$
$latex {{r}^2}=47,75$
$latex r=6,91$
O raio do círculo é 6,91 cm.
Perímetro e área de um círculo – Exercícios para resolver
Resolva os exercícios a seguir usando o que você aprendeu sobre o perímetro e a área de um círculo. Clique em “Verificar” para verificar se você acertou a resposta.
Veja também
Interessado em aprender mais sobre perímetro e área de figuras geométricas? Você pode visitar estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
