A equação da reta tangente a um círculo é encontrada usando a forma y=mx+b. Por outro lado, podemos encontrar o declive m, determinando o declive do raio com o centro do círculo e o ponto tangente. Depois, utilizamos o ponto tangente para encontrar o valor de b.
A seguir, aprenderemos a encontrar a equação da tangente a um círculo. Depois, aplicaremos este processo para resolver alguns exercícios práticos.
Como encontrar a equação da reta tangente a um círculo
Para encontrar a equação da tangente a um círculo, recordamos que podemos encontrar a equação de qualquer reta utilizando a forma $latex y=mx+b$, onde m é o declive e b é a intercepção em y.
Neste caso, o declive m é encontrado utilizando o declive do raio e a intercepção y é encontrada utilizando as coordenadas do ponto tangente.
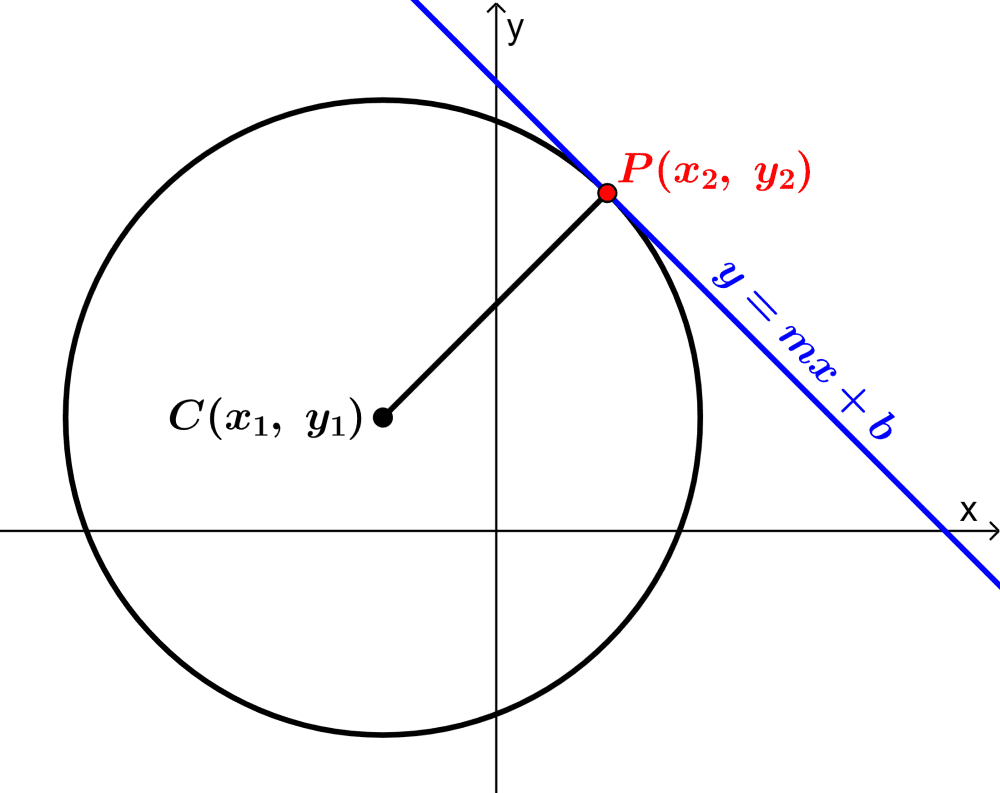
Seguimos então os passos seguintes:
1. Encontrar as coordenadas do centro do círculo.
Se a equação for dada na sua forma padrão, $latex r^2=(x-a)^2+(x-b)^2$, o centro é $latex (a,~b)$. Se tivermos uma equação geral do círculo, temos de completar o quadrado de x e y para encontrar o centro.
2. Encontrar o declive do raio do círculo.
Para isso, usamos a fórmula de declive $latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ com as coordenadas do ponto tangente e o centro do círculo.
3. Encontrar o declive da reta tangente.
Dado que o raio e a tangente são perpendiculares, o declive da tangente é igual à recíproca negativa do declive do raio.
4. Encontrar o valor de b, a intercepção em y.
Para isso, utilizamos o declive do passo 3 e as coordenadas do ponto tangente na forma $latex y=mx+b$ e resolvemos para b.
Exercícios resolvidos sobre a equação da tangente a um círculo
EXERCÍCIO 1
Encontrar a equação da reta tangente ao círculo $latex (x+2)^2+(y-3)^2=4$ no ponto $latex P=(0,~4)$.
Solução
Passo 1: Uma vez que a equação do círculo está na forma padrão, podemos facilmente ver que o centro é igual a $latex (-2, 3)$.
Passo 2: Usamos $latex (x_{1},~y_{1})=(-2, 3)$ e $latex (x_{2},~y_{2})=(0, ~4)$ para encontrar o declive do raio do círculo:
$$m_{r}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
$$=\frac{4-3}{0+2}$$
$$=\frac{1}{2}$$
Passo 3: O declive da reta tangente é:
$$m=-\frac{1}{m_{r}}$$
$$m=-2$$
Passo 4: Para encontrar o valor de b, usamos $latex (x,~y)=(0,~4)$:
$latex y=mx+b$
$latex 4=-2(0)+b$
$latex b=4$
A equação da reta tangente ao círculo a $latex (0, ~4)$ é $latex y=-2x+4$.
EXERCÍCIO 2
Qual é a equação da reta tangente ao círculo $latex (x-1)^2+(y-2)^2=10$ no ponto $latex P=(4,~3)$?
Solução
Passo 1: Temos a equação do círculo na sua forma padrão, pelo que vemos que o centro é $latex (1, 2)$.
Passo 2: Encontramos o declive do raio do círculo usando as coordenadas $latex (x_{1},~y_{1})=(1, 2)$ e $latex (x_{2},~y_{2})= (4, ~3)$ para encontrar o declive do raio do círculo:
$$m_{r}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
$$=\frac{3-2}{4-1}$$
$$=\frac{1}{3}$$
Passo 3: O declive da reta tangente é:
$$m=-\frac{1}{m_{r}}$$
$$m=-3$$
Passo 4: Usando o ponto tangente $latex (x,~y)=(4,~3)$, encontramos o valor de b:
$latex y=mx+b$
$latex 3=-3(4)+b$
$latex b=15$
A equação da reta tangente ao círculo a $latex (4, ~3)$ é $latex y=-3x+15$.
EXERCÍCIO 3
Encontrar a equação da reta tangente ao círculo $latex x^2+y^2+2x-4y-20=0$ no ponto $latex P=(2, 6)$.
Solução
Passo 1: Neste caso, a equação do círculo está na sua forma geral. Depois, escrevemo-la na sua forma padrão, completando o quadrado de ambas as variáveis:
$latex x^2+y^2+2x-4y-20=0$
$latex x^2+2x+y^2-4y-20=0$
$$(x+1)^2-1+(y-2)^2-4-20=0$$
$latex (x+1)^2+(y-2)^2=25$
Agora, vemos que o centro é $latex (-1, ~2)$.
Passo 2: O declive do raio do círculo é
$$m_{r}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
$$=\frac{6-2}{2+1}$$
$$=\frac{4}{3}$$
Passo 3: O declive da reta tangente é:
$$m=-\frac{1}{m_{r}}$$
$$m=-\frac{3}{4}$$
Passo 4: Para encontrar o valor de b, utilizamos as coordenadas do ponto tangente $latex (x,~y)=(2,~6)$:
$latex y=mx+b$
$latex 6=-\frac{3}{4}(2)+b$
$latex b=\frac{15}{2}$
A equação da reta tangente ao círculo em $latex (2, ~6)$ é $latex y=-\frac{3}{4}x+\frac{15}{2}$.
EXERCÍCIO 4
Qual é a equação da reta tangente ao círculo $latex x^2+y^2-2x-6y+8=0$ no ponto $latex P=(2, 2)$?
Solução
Passo 1: Escrevendo a equação do círculo na sua forma padrão, temos:
$latex x^2+y^2-2x-6y+8=0$
$latex x^2-2x+y^2-6y+8=0$
$$(x-1)^2-1+(y-3)^2-9+8=0$$
$latex (x-1)^2+(y-3)^2=2$
O centro do círculo é $latex (1, ~3)$.
Passo 2: Encontrando o declive do raio do círculo, temos:
$$m_{r}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
$$=\frac{2-3}{2-1}$$
$latex =-1$
Passo 3: O declive da reta tangente é:
$$m=-\frac{1}{m_{r}}$$
$$m=1$$
Passo 4: Usamos o ponto tangente para encontrar o valor de b:
$latex y=mx+b$
$latex 2=1(2)+b$
$latex b=0$
A equação da reta tangente ao círculo a $latex (2, ~2)$ é $latex y=x$.
EXERCÍCIO 5
Encontrar a equação da reta tangente ao círculo $latex x^2+y^2+4x+6y-21=0$ no ponto $latex P=(1, ~2)$.
Solução
Passo 1: Encontrando a forma padrão da equação do círculo dado, temos:
$latex x^2+y^2+4x+6y-21=0$
$latex x^2+4x+y^2+6y-21=0$
$$(x+2)^2-4+(y+3)^2-9-21=0$$
$latex (x+2)^2+(y+3)^2=34$
O centro do círculo é $latex (-2,~-3)$.
Passo 2: Encontrando o declive do raio do círculo, temos:
$$m_{r}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
$$=\frac{2+3}{1+2}$$
$$=\frac{5}{3}$$
Passo 3: O declive da reta tangente é:
$$m=-\frac{1}{m_{r}}$$
$$m=-\frac{3}{5}$$
Passo 4: Usamos $latex (x,~y)=(1,~2)$ para encontrar o valor de b:
$latex y=mx+b$
$latex 2=-\frac{3}{5}(1)+b$
$latex b=\frac{13}{5}$
A equação da reta tangente ao círculo em $latex (1, ~2)$ é $latex y=-\frac{3}{5}x+\frac{13}{5}$.
EXERCÍCIO 6
Qual é a equação da reta tangente ao círculo $latex x^2+y^2+6x-4y+8=0$ no ponto $latex P=(-1, 1)$?
Solução
Passo 1: Escrevendo a equação do círculo na sua forma padrão, temos:
$latex x^2+y^2+6x-4y+8=0$
$latex x^2+6x+y^2-4y+8=0$
$$(x+3)^2-9+(y-2)^2-4+8=0$$
$latex (x+3)^2+(y-2)^2=5$
Agora, vemos que o centro do círculo é $latex (-3, ~2)$.
Passo 2: O declive do raio do círculo é
$$m_{r}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
$$=\frac{1-2}{-1+3}$$
$$=-\frac{1}{2}$$
Passo 3: O declive da reta tangente é:
$$m=-\frac{1}{m_{r}}$$
$latex m=2$
Passo 4: Para encontrar o valor de b, usamos $latex (x,~y)=(-1,~1)$:
$latex y=mx+b$
$latex 1=2(-1)+b$
$latex b=3$
A equação da reta tangente ao círculo a $latex (-1, ~1)$ é $latex y=2x+3$.
Equação da tangente à circunferência – Exercícios para resolver


Encontre a equação da tangente ao próximo círculo no ponto (1, 4):$$ x^2-6x+y^2-6y+18=5$$
Escreva a equação na caixa.
Veja também
Interessado em aprender mais sobre círculos? Você pode olhar para estas páginas:



