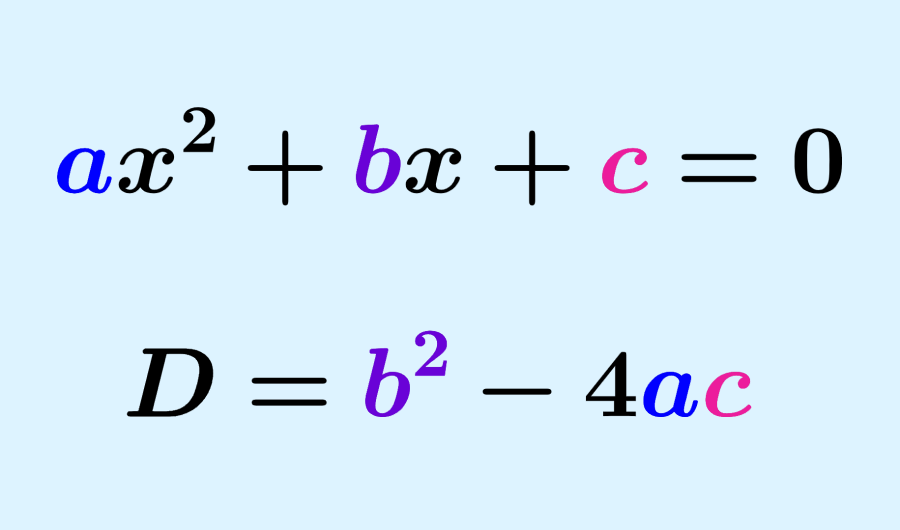Equações quadráticas são equações algébricas que têm a forma ax²+bx+c=0. Considerando esta forma, o discriminante de uma equação quadrática é o valor b²-4ac. Este valor entra na raiz quadrada da fórmula de Bhaskara e determina o tipo de soluções que teremos.
A seguir, saberemos tudo relacionado ao discriminante de uma equação quadrática. Além disso, usaremos sua fórmula para resolver alguns exercícios práticos.
Fórmula do discriminante de uma equação quadrática e aplicações
Quando temos equações quadráticas escritas na forma $latex a{{x}^2}+bx+c=0$, o discriminante é dado pela seguinte fórmula:
| $latex D=b^2-4ac$ |
O valor do discriminante nos dá informações sobre o tipo de raízes que obteremos na equação quadrática dada. Então, temos o seguinte:
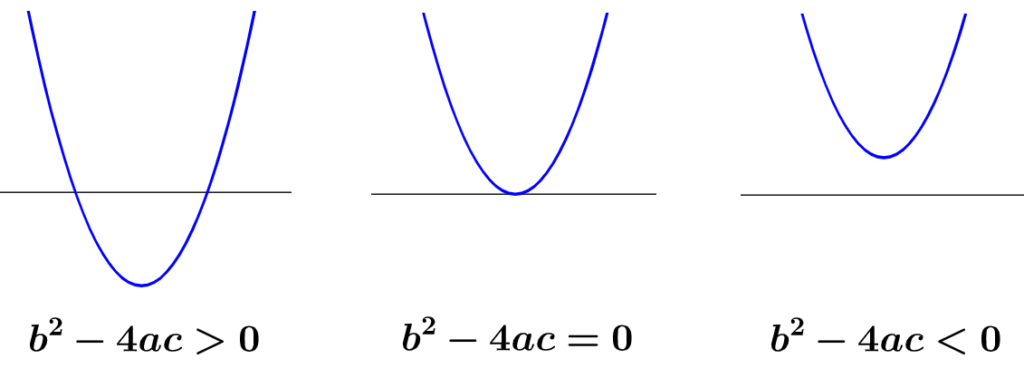
- Quando $latex b^2-4ac>0$, a equação quadrática tem duas raízes reais.
- Quando $latex b^2-4ac<0$, a equação quadrática não tem raízes reais.
- Quando $latex b^2-4ac=0$, a equação quadrática tem uma raiz repetida.
Podemos entender isso melhor se lembrarmos que a fórmula de Bhaskara, que nos permite resolver qualquer equação quadrática, é a seguinte:
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
Assim, podemos ver que o discriminante é a expressão dentro da raiz quadrada da fórmula de Bhaskara. Portanto, quando o valor dentro da raiz quadrada for positivo, teremos duas raízes reais.
Por outro lado, quando o valor dentro da raiz quadrada for negativo, não teremos raízes reais (mas teremos raízes imaginárias ou complexas). E finalmente, se o discriminante for igual a zero, teremos uma única raiz.
O discriminante de uma equação quadrática indica se o gráfico da equação quadrática intercepta o eixo x em dois pontos diferentes, não intercepta o eixo x ou toca o eixo x em apenas um ponto, como vemos no diagrama a seguir :
Discriminante de uma equação quadrática – Exercícios resolvidos
A fórmula para o discriminante de uma equação quadrática é usada para resolver os exercícios a seguir. Cada exercício tem sua respectiva solução, mas tente resolver os exercícios você mesmo.
EXERCÍCIO 1
Encontre o discriminante da equação $latex x^2+4x+5=0$.
Solução
Usando os valores $latex a=1$, $latex b=4$ e $latex c=5$ na fórmula discriminante, temos:
$latex D=b^2-4ac$
$latex D=4^2-4(1)(5)$
$latex D=16-20$
$latex D=-4$
O discriminante da equação é $latex D=-4$.
EXERCÍCIO 2
Determine o discriminante da equação $latex -2x^2+4x-2$.
Solução
Temos os valores $latex a=-2$, $latex b=4$, e $latex c=-2$. Usando esses valores na fórmula discriminante, temos:
$latex D=b^2-4ac$
$latex D=4^2-4(-2)(-2)$
$latex D=16-16$
$latex D=0$
O discriminante da equação é $latex D=0$.
EXERCÍCIO 3
Use o discriminante para mostrar que a equação $latex 5x^2+4x+10=0$ não tem soluções reais.
Solução
Usando a fórmula discriminante com os valores $latex a=5$, $latex b=4$ e $latex c=10$, temos:
$latex D=b^2-4ac$
$latex D=4^2-4(5)(10)$
$latex D=16-200$
$latex D=-184$
O discriminante é negativo, então a equação não tem raízes reais. Isso ocorre porque temos um número negativo dentro da raiz quadrada da fórmula geral.
EXERCÍCIO 4
Quantas raízes reais tem a equação $latex -3x^2-2x+5=0$?
Solução
Usamos os valores $latex a=-3$, $latex b=-2$ e $latex c=5$ na fórmula discriminante e temos:
$latex D=b^2-4ac$
$latex D=(-2)^2-4(-3)(5)$
$latex D=4+60$
$latex D=64$
O discriminante é positivo, então a equação tem duas raízes reais.
EXERCÍCIO 5
Encontre o valor de k na equação $latex 3x^2-6x+k=0$, supondo que a equação tenha apenas uma raiz repetida.
Solução
Neste caso, temos $latex a=3$, $latex b=-6$ e $latex c=k$. Para encontrar o valor de k, temos que usar a fórmula discriminante que tem valor igual a zero, pois a equação tem apenas uma raiz:
$latex D=b^2-4ac=0$
$latex (-6)^2-4(3)(k)=0$
$latex 36-12k=0$
$latex -12k=-36$
$latex k=3$
Então, se a equação quadrática tem uma única raiz repetida, o valor de k é 3.
EXERCÍCIO 6
Encontre o valor de k na equação $latex kx^2+5x-4=0$ se a equação tiver apenas uma raiz.
Solução
Temos os valores $latex a=k$, $latex b=5$ e $latex c=-4$. Usamos a fórmula discriminante, igualamos a zero e resolvemos para k:
$latex D=b^2-4ac=0$
$latex (5)^2-4(k)(-4)=0$
$latex 25+16k=0$
$latex 16k=-25$
$latex k=-\frac{25}{16}$
Então, se a equação quadrática tem uma única raiz repetida, o valor de k é 25/16.
EXERCÍCIO 7
Prove que $latex y=2x^2+7x+7$ é sempre positivo usando o discriminante.
Solução
Usando os valores $latex a=2$, $latex b=7$ e $latex c=7$ na fórmula discriminante, temos:
$latex D=b^2-4ac$
$latex D=(7)^2-4(2)(7)$
$latex D=49-56$
$latex D=-7$
Como o discriminante é negativo, a equação não tem raízes reais. Portanto, a função não corta o eixo x. Além disso, como o coeficiente de $latex x^2$ é positivo, o gráfico da função se abre e está sempre acima do eixo x, então os valores são sempre positivos.
Discriminante de uma equação quadrática – Exercícios para resolver
Use a fórmula para o discriminante de uma equação quadrática para resolver os seguintes exercícios práticos.
Veja também
Interessado em aprender mais sobre equações quadráticas? Você pode olhar para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
