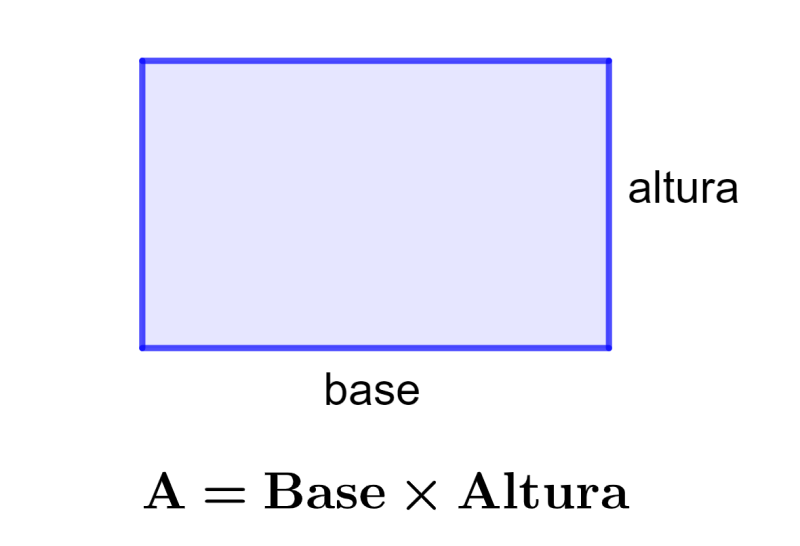
Um retângulo é uma figura bidimensional com quatro lados, quatro vértices e quatro ângulos retos. Os dois lados opostos do retângulo são iguais e paralelos um ao outro. A área de um retângulo é o espaço coberto pela figura. Alternativamente, o espaço dentro do perímetro do retângulo é a área.
A seguir, veremos por que a área de um retângulo é o produto de seus dois lados. Além disso, veremos vários exercícios de áreas de um retângulo para dominar o uso da fórmula.
GEOMETRIA
Relevante para…
Aprender a encontrar a área de um retângulo com exercícios.
GEOMETRIA
Relevante para…
Aprender a encontrar a área de um retângulo com exercícios.
Qual é a fórmula para encontrar a área de um retângulo?
A fórmula para calcular a área de um retângulo é A = Base × Altura. A área de um retângulo depende de seus lados. Basicamente, a fórmula da área é igual ao produto da base pela altura do retângulo.
Já quando falamos sobre o perímetro do retângulo, sabemos que ele é igual à soma de seus quatro lados. Portanto, podemos dizer que a região delimitada pelo perímetro do retângulo é a sua área.
O quadrado é um caso especial de retângulo, que tem todos os lados iguais. Então, como todos os lados são iguais, a área do quadrado será igual ao comprimento de um de seus lados ao quadrado.
| Área de retângulo = Base × Altura $latex A=b\times a$ |
A área de qualquer retângulo é calculada uma vez que sua base e altura são conhecidas. Multiplicando a base pela altura, a área do retângulo obtém uma dimensão em unidades quadradas.
Como calcular a área de um retângulo?
Podemos encontrar a área de um retângulo seguindo os seguintes passos:
Passo 1: Identifique as dimensões da base e a altura das informações fornecidas.
Passo 2: Multiplique os valores de base e altura.
Passo 3: Escreva a resposta em unidades quadradas.
Por que a área de um retângulo é igual à base vezes a altura?
No retângulo abaixo, sua diagonal o divide em dois triângulos retângulos iguais. Portanto, a área do retângulo será igual à soma das áreas desses dois triângulos.
Temos o retângulo ABCD:
A diagonal AC divide o retângulo em dois triângulos retângulos, $latex \Delta$ABC e $latex \Delta$ADC.
Sabemos que $latex \Delta$ABC e $latex \Delta$ADC são triângulos congruentes, então temos:
⇒ Área (ABCD) = Área (ABC) + Área (ADC)
⇒ Área (ABCD) = 2 × Área (ABC)
⇒ Área (ABC) = $latex \frac{1}{2}$ × base × altura
⇒ Área (ABCD) = 2 × ($latex \frac{1}{2}$ × b × h)
⇒ Área (ABCD) = b × h
Como calcular os lados de um retângulo conhecendo a área?
Se conhecermos a área de um retângulo, podemos calcular seus lados usando a fórmula para a área de um retângulo. A fórmula para um retângulo é A = base × altura.
No caso de um quadrado, isso se torna muito fácil, pois um quadrado é um retângulo especial que tem todos os seus lados iguais, então sua área é igual a um de seus lados ao quadrado.
Portanto, se tivermos a área de um quadrado, podemos calcular seus lados aplicando a raiz quadrada da área. Por exemplo, se temos que a área de um quadrado é de 100 metros quadrados, podemos aplicar a raiz quadrada para obter 10 metros, que é o comprimento de seus lados.
No caso de um retângulo com diferentes comprimentos de lado, isso é um pouco mais complicado, pois precisamos conhecer a área e um de seus lados para calcular o comprimento do outro lado.
Por exemplo, se a área de um retângulo é igual a 100 metros quadrados e um de seus lados é 20 metros, simplesmente dividimos 100 por 20 para obter o comprimento do outro lado. Portanto, o comprimento do outro lado é de 5 metros
Alternativamente, podemos encontrar o comprimento dos lados de um retângulo se conhecermos sua área e as proporções de seus lados. Por exemplo, se tivermos que a área de um retângulo é igual a 100 metros quadrados e as proporções de seus lados são 5:20, sabemos que um de seus lados tem 5 metros e o outro tem 20 metros.
Exercícios de área de um retângulo resolvidos
Os exercícios a seguir usam a fórmula para a área de um retângulo para obter a resposta. Cada exercício tem sua respectiva solução, mas é recomendável que você tente resolver os exercícios antes de olhar a resposta.
EXERCÍCIO 1
Encontre a área de um retângulo que tem uma base de 20 cm e uma altura de 12 cm.
Solução
Temos os seguintes dados:
- Base = 20 cm
- Altura = 12 cm
Temos a fórmula A = base × altura. Substituindo pelas informações fornecidas, temos:
$latex 20 \times 12 = 240$
Portanto, a área é de 240 cm².
EXERCÍCIO 2
Encontre a área de um quadro negro com dimensões de 140 cm na base e 90 cm de altura.
Solução
Temos as seguintes informações:
- Base = 140 cm
- Altura = 90 cm
Temos a fórmula A = base × altura. Então, substituímos para obter:
$latex 140 \times 90 = 12.600$
Portanto, a área do quadro é de 12.600 cm².
EXERCÍCIO 3
A base de um retângulo tem 20 cm e sua área é 120 cm². Qual é o comprimento da sua altura?
Solução
Temos as seguintes informações:
- Base = 20 cm
- Área = 120 cm²
Podemos usar a fórmula A = base × altura. Então, substituímos para obter:
base $latex = \frac{120}{20}=6$
Portanto, a altura é de 6 cm.
EXERCÍCIO 4
Um quadrado tem lados de 8 m de comprimento. Qual é a sua área?
Solução
Temos as seguintes informações:
- Lado = 8 m
Sabemos que um quadrado é um retângulo com lados iguais, então sua área pode ser encontrada usando A = lado². Então, substituímos para obter:
$latex A={{8}^2}=64$
Portanto, a área do quadrado é de 64 m².
EXERCÍCIO 5
A área de um quadrado é igual a 8100 cm². Qual é o comprimento de um de seus lados?
Solução
Temos as seguintes informações:
- Área = 8100 cm²
Sabemos que um quadrado é um retângulo com lados iguais, então podemos usar a fórmula A = lado². Então, nós substituímos para obter:
lado $latex = \sqrt{8100}= 90$
Portanto, o comprimento de um dos lados é de 90 cm.
Exercícios de área de um retângulo para resolver
Teste o que você aprendeu sobre a área de um retângulo com os exercícios a seguir.
Veja também
Você quer aprender mais sobre retângulos? Olha para estas páginas: