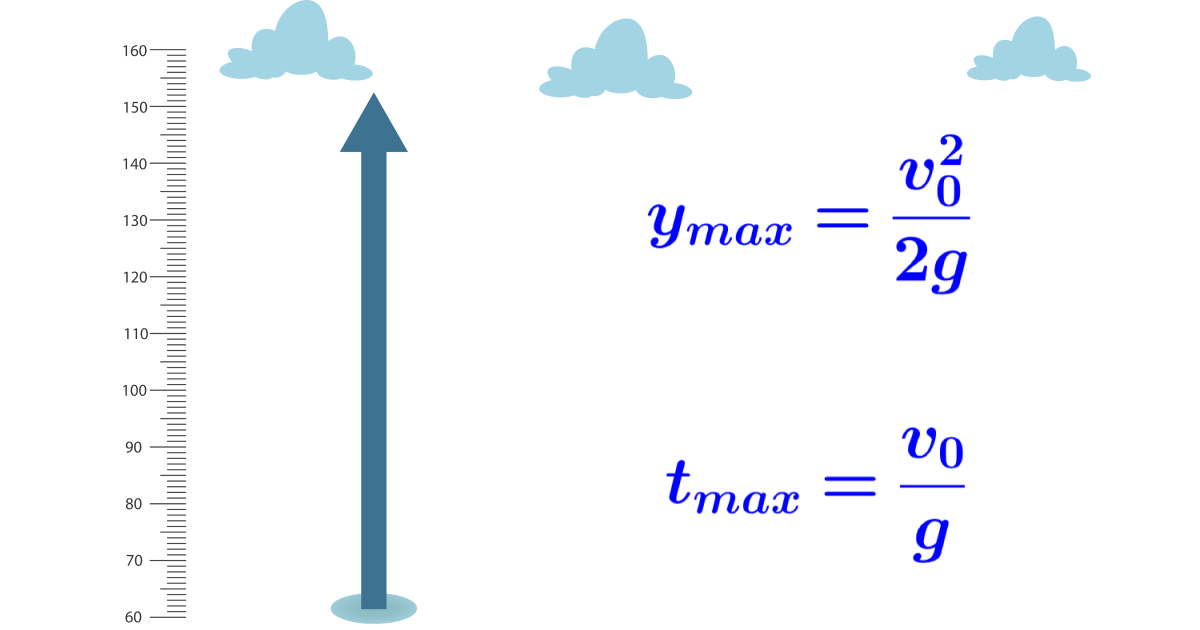
O lançamento vertical é um caso específico de movimento na física, em que um objeto é lançado verticalmente para cima ou para baixo, sem componente horizontal de velocidade. Nesse tipo de movimento, o objeto está sujeito apenas à força da gravidade, que atua para baixo com uma aceleração constante denotada por “g” (aproximadamente 9,8 m/s² na Terra).
Aqui, aprenderemos sobre as fórmulas que podemos usar para prever o comportamento de objetos em lançamento vertical e as usaremos para resolver problemas relacionados a esse tipo de movimento.
FÍSICA
Relevante para…
Aprender sobre o lançamento vertical na física com exercícios.
FÍSICA

Relevante para…
Aprender sobre o lançamento vertical na física com exercícios.
Fórmulas para o lançamento vertical
O lançamento vertical é qualquer movimento vertical acelerado sob a ação da gravidade, quer o objeto se desloque para cima ou para baixo (queda livre). A resistência do ar, que tende a desacelerar o movimento, é ignorada. Esse é um movimento extremamente comum na natureza e na vida cotidiana.
O lançamento vertical é considerado queda livre, mesmo que tenha velocidade inicial, pois a queda livre é o movimento de um objeto acelerado apenas sob a ação da gravidade.
Portanto, a equação para a posição em função do tempo em um lançamento vertical é a mesma que para qualquer movimento retilíneo com aceleração constante. Esta aceleração é denotada $latex g$ e comumente seu valor é $latex g= 9,8\hspace{1mm}\dfrac{m}{s^2}$, assumindo que o movimento ocorre nas proximidades da Terra.
Lançamento vertical: fórmula para a posição
Em todos os casos, se for escolhido um sistema de referência no qual a direção vertical descendente seja negativa, a equação para a posição de um objeto em função do tempo adquire a forma:
$$y(t)=y_{0}+v_{0}t-\frac{1}{2}gt^2$$
Entretanto, em alguns casos, será mais conveniente considerar a direção vertical descendente como positiva, portanto, deve-se tomar cuidado para ser consistente com a escolha dos sinais.
Na equação mostrada, $latex y(t)$ denota a posição vertical em função do tempo decorrido e $latex y_{0}$ é a posição inicial, que pode ser escolhida para ser igual a 0 no ponto de lançamento, simplificando a equação a:
$$y(t)=v_{0}t-\frac{1}{2}gt^2$$
O sinal da velocidade inicial pode ser positivo ou negativo, dependendo se o objeto é impulsionado para cima ou para baixo. Ou seja, se o objeto for impulsionado para cima, a velocidade inicial é positiva e, à medida que o projétil sobe, sua magnitude diminui aos poucos até parar. Nesse ponto, o objeto atinge sua altura máxima.
Diversas aplicações exigem o conhecimento dessa altura máxima, para a qual não é difícil desenvolver uma expressão:
Lançamento vertical: fórmula para a altura máxima
A partir da equação que relaciona velocidade e posição para um movimento uniformemente acelerado:
$$v^2 =v_0^2 – 2gy$$
Fazendo $latex v=0$, resulta na altura máxima $latex y_{max}$, dada por:
$$0 =v_0^2 – 2gy_{max}$$
Portanto:
$$y_{max}=\frac{v_0^2}{2g}$$
Como pode ser visto, a altura máxima depende da velocidade inicial dada ao projétil. Quanto maior for essa velocidade, mais altura o objeto alcançará.
Lançamento vertical: fórmula para o tempo máximo
O tempo máximo é o tempo que o projétil leva para atingir sua altura máxima. Ele pode ser calculado a partir da equação que relaciona velocidade e tempo:
$$v=v_0-gt$$
Quando o projétil atinge a altura máxima, ele para momentaneamente e começa a descer, só aí é atingido o tempo máximo $latex t_{max}$:
$$0=v_0-gt_{max}$$
$$t_{max}=\frac{v_0}{g}$$
Quanto maior a velocidade inicial do objeto, mais tempo ele levará para atingir a altura máxima.
Exercícios resolvidos sobre o lançamento vertical em Física
Nota: Nos exercícios a seguir, a resistência do ar é ignorada e o valor da aceleração da gravidade é tomado como $latex g=9,8\frac{m}{s}$.
EXERCÍCIO 1
Uma pedra é lançada verticalmente para cima com uma velocidade inicial de 26,2 m/s, que chega até a borda do telhado de um edifício. Calcule:
a) A altura H do edifício.
b) O tempo que permanece no ar.
c) Quantos andares tem o edifício? Suponha que cada andar tenha 3,5 m de altura.
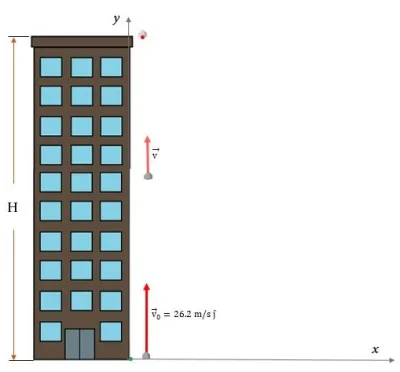
Solução
a) Para encontrar a altura do edifício, sabendo a velocidade inicial, usamos:
$$h_{max}=H=\frac{v_0^2}{2g}$$
O sistema de referência é usado com a origem no ponto inicial e a direção vertical positiva para cima.
Substituindo os valores fornecidos, obtemos:
$$H=\frac{\left(26,2\hspace{1mm}\dfrac{m}{s}\right)^2}{2\times 9,8\hspace{1mm}\dfrac{m}{s^2}}=35,02\hspace{1mm}m$$
b) A duração do tempo pode ser encontrada em:
$$t=\frac{v_0}{g}$$
$$t=\frac{26,2\hspace{1mm}\dfrac{m}{s}}{9,8\hspace{1mm}\dfrac{m}{s^2}}=2,7\hspace{1mm}s$$
c) Dividir a altura do edifício pela altura de cada andar resulta em n, o número de andares:
$$n=\frac{35,2}{3,5}\approx 10\hspace{1mm}andares$$
EXERCÍCIO 2
Uma bola é lançada verticalmente para cima até atingir uma altura máxima de 20 m.
a) Qual é a velocidade inicial a ser fornecida?
b) Quanto tempo ele durará no ar?
Solução
a) A partir da equação que relaciona a altura máxima com a velocidade inicial, resolvemos a velocidade inicial:
$$h_{max}=\frac{v_0^2}{2g}\Rightarrow v_0=\sqrt{2gh_{max}}$$
Substituindo o valor dado na declaração para a altura máxima, obtemos:
$$v_0=\sqrt{2\times\hspace{1mm}9,8\dfrac{m}{s^2}\times 20\hspace{1mm}m}=19,8\dfrac{m}{s}$$
b) Como a bola retorna ao seu ponto de partida, o tempo que ela durará no ar, ou tempo de voo $latex t_{voo}$, é o dobro do tempo necessário para atingir a altura máxima $latex t_{max}$:
$$t_{voo}=2\cdot t_{max}=\frac{2v_0}{g}=\frac{2\times 19,8\dfrac{m}{s}}{9,8\dfrac{m}{s^2}}=4,04\hspace{1mm}s$$
EXERCÍCIO 3
Do telhado de um edifício, localizado 10 m acima do solo, dois objetos são lançados verticalmente para cima, com um intervalo de tempo de 2 s entre cada lançamento. A velocidade inicial do primeiro objeto é de 80 m/s e a do segundo objeto é de 100 m/s.
a) Depois de quanto tempo os objetos estarão na mesma altura?
b) Qual será a altura?
c) Qual será a velocidade de cada objeto nesse instante?
Solução
a) Sejam $latex y_1$ e $latex y_2$ as respectivas posições de cada objeto, e sejam $latex t_1$ e $latex t_2$ seus respectivos tempos. Chamando $latex t$ o tempo do primeiro objeto, o tempo do segundo será atrasado em 2 segundos, então $latex t_2=t-2$.
Para que o encontro ocorra, as posições e os tempos dos objetos devem ser os mesmos:
$$y_1=y_2\Rightarrow v_{01}t-\frac{1}{2}gt^2= v_{02}(t-2)-\frac{1}{2}g(t-2)^2$$
$$ 80t-4,9t^2= 100(t-2)-4,9(t-2)^2$$
Então, a seguinte equação é obtida:
$$ 80t-4,9t^2= 100t-200-4,9t^2+19,6t-19,6$$
$$-20t-19,6t=-200-19,6$$
$$39,6t=219,2\Rightarrow t =\frac{219,6}{39,6}\hspace{1mm}s=5,5\hspace{1mm}s$$
b) A altura pode ser encontrada substituindo esse resultado na equação da posição dos objetos, por exemplo:
$$y_1=80t-4,9t^2=(80\times 5,5-4,9\times 5,5^2)\hspace{1mm}m=291,8\hspace{1mm}m $$
c) A equação da velocidade de qualquer um dos objetos é:
$$v(t)=v_0-gt$$
Portanto, para cada um deles:
$$v_1=80\frac{m}{s}-\left(9,8\frac{m}{s^2}\times 5,5\hspace{1mm}s\right)=26,1\hspace{1mm}\frac{m}{s}$$
$$v_2=100\frac{m}{s}-\left(9,8\frac{m}{s^2}\times 5,5\hspace{1mm}s\right)=46,1\hspace{1mm}\frac{m}{s}$$
EXERCÍCIO 4
Um balão está a 80 m, subindo a uma velocidade constante de 58 m/s, quando subitamente libera um pacote.
a) Quanto tempo leva para o pacote chegar ao solo?
b) Qual é sua altura máxima?
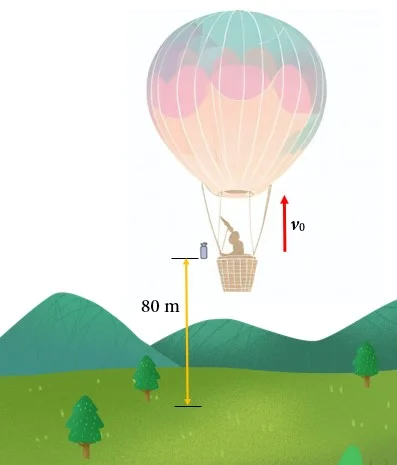
Solução
a) O pacote deixa o balão com a velocidade inicial $latex v_{0}$. Tomando a origem do sistema de coordenadas no local onde o pacote é liberado, a equação de posição é
$$y(t)=v_0t-\frac{1}{2}gt^2$$
E substituindo a velocidade inicial indicada na declaração, o resultado é o seguinte:
$$y(t)=58t-4.9t^2$$
O solo está na posição $latex y=-80\hspace{1mm}m$, o que leva à seguinte equação quadrática:
$$-80=58t-4,9t^2$$
Cujas soluções são:
$latex t_1=-1,25$
$latex t_2=13,1$
Somente a solução positiva faz sentido, portanto, o pacote permanece no ar por um tempo $latex t_{voo}=13,1\hspace{1mm}s$.
b) Como a velocidade inicial do pacote é ascendente, ela é considerada positiva. O pacote subirá uma certa altura antes de descer.
A altura máxima em relação à posição em que foi liberado é:
$$h_{max}=\frac{v_0^2}{2g}=\frac{\left(58\dfrac{m}{s}\right)^2}{2\times 9,8\dfrac{m}{s^2}}=171,6\hspace{1mm}m$$
Então, a altura máxima, medida em relação ao solo, é:
$$H_{max}=(171,6+80)\hspace{1mm}m=251,6 \hspace{1mm}m$$
EXERCÍCIO 5
Um foguete de teste é lançado verticalmente com velocidade inicial de 75,0 m/s e se afasta da plataforma de lançamento com aceleração de 5,50 m/s2. Depois de um tempo, o foguete esgota o combustível e seu motor desliga a uma altitude de 1,20 km, sendo então liberado para a ação da gravidade.
a) Quanto tempo o foguete fica no ar?
b) Qual é a altitude máxima atingida pelo foguete?
c) Qual é a velocidade do foguete logo antes de atingir o solo?
Solução
a) O movimento é vertical e ocorre em duas etapas: a primeira em que o foguete é impulsionado pela aceleração proporcionada pelo seu combustível e sobe $latex 1,20\hspace{1mm} km = 1200 \hspace{1mm}m$ .
A segunda começa quando o combustível se esgota e o foguete fica sob a ação da gravidade.
No primeiro estágio, a aceleração impulsiona o foguete para cima e recebe um sinal de +, enquanto no segundo estágio, a aceleração é a da gravidade, direcionada verticalmente para baixo e com um sinal de -.
Primeiro estágio
A equação para a posição no primeiro estágio é:
$$ y=75t+\left(\frac{1}{2}\right)5,5t^2=75t+2,75t^2$$
Onde a origem do sistema de coordenadas foi tomada no ponto de lançamento.
Resolvendo a equação em $latex t$ para $latex y=1200$, resulta:
$$2,75t^2+75t-1200=0$$
A solução positiva é:
$$t=11,3\hspace{1mm}s$$
Nesse momento, a velocidade do foguete é:
$$v=75+5,5t=(75+5,5\times 11,3)\hspace{1mm}\frac{m}{s}=137,15\hspace{1mm}\frac{m}{s} $$
Segundo estágio
O próximo estágio ocorre sob a ação da gravidade e começa com a velocidade que tinha no final do primeiro estágio, que acabou de ser calculada.
A nova equação de posição será:
$$ y=1200+137,15t-4,9t^2$$
O tempo necessário para retornar a $latex y = 0$ é obtido pela solução da equação:
$$ 1200+137,15t-4,9t^2=0$$
Cuja solução é:
$$t=35,0\hspace{1mm}s$$
Portanto, o foguete permaneceu no ar por um tempo $latex t_{total}$:
$$t_{total}=11,3\hspace{1mm}s+35,0\hspace{1mm}s=46,3\hspace{1mm}s$$
b) Durante o primeiro estágio do movimento, o foguete subiu $latex h_1= 1200\hspace{1mm}m$. Então, agora calculamos a altura que ela atinge durante o segundo estágio, que chamaremos de $latex h_2$:
$$h_2=h_{max}=\frac{v_0^2}{2g}=\left(\frac{137,15^2}{2\times 9,8}\right)\hspace{1mm}{m}=964,6\hspace{1mm}{m}$$
Portanto:
$$h_2=964,6\hspace{1mm}{m}$$
O foguete sobe a uma altura total $latex H$ de:
$$H=1200\hspace{1mm}{m}+964,6\hspace{1mm}{m}=2164,6\hspace{1mm}{m}$$
c) A equação para a velocidade no segundo estágio é:
$$v(t)=137,15-9,8t$$
Portanto, a velocidade quando ele atinge o solo é:
$$v(t)=(137,15-9,8\times 35,0)\hspace{1mm}\frac{m}{s}=-205,85\hspace{1mm}\frac{m}{s}$$
EXERCÍCIO 6
Uma bola é lançada do telhado de um prédio de 80 m e, dois segundos depois, outra bola idêntica é lançada do chão, verticalmente para cima, com velocidade inicial de 20 m/s. Calcule:
a) Em que momento eles se cruzam?
b) Em que altura ocorre o cruzamento?
Solução
a) A origem do sistema de coordenadas pode ser escolhida no telhado de forma que o solo fique na posição $latex y_{solo}=-80\hspace{1mm}m$.
Para a bola 1, a equação de posição é:
$latex y_1=-4,9t^2$
Para a bola 2, que começa 2 segundos depois da bola 1 e tem uma velocidade inicial ascendente de $latex 20\frac{m}{s}$, a equação de posição é:
$latex y_2=-80+20(t-2)-4,9(t-2)^2$
Para que as bolas se cruzem, elas devem ocupar a mesma posição vertical:
$$y_1=y_2\Rightarrow -4,9t^2=-80+20(t-2)-4,9(t-2)^2$$
Usando álgebra:
$$-4,9t^2=-80+20t-40-4,9(t^2-4t+4)\Rightarrow $$
$$-4,9t^2=-80+20t-40-4,9t^2+19,6t-19,6$$
Após simplificar os termos semelhantes:
$$39,6t=139,6\Rightarrow t=\frac{139,6}{39,6}\hspace{1mm}s=3,5\hspace{1mm}s$$
b) A localização da interseção pode ser encontrada substituindo esse tempo em qualquer uma das equações de posição, por exemplo:
$$ y_1=(-4,9\times 3,5^2)\hspace{1mm}m=-60\hspace{1mm}m$$
Isso significa que, medida a partir do solo, a altura em que a interseção ocorre é:
$$h_{cruzamento}=(80-60)\hspace{1mm}m=20\hspace{1mm}m$$
EXERCÍCIO 7
A Mulher Maravilha está em uma ponte, enquanto um caminhão-plataforma vem em sua direção na rodovia abaixo, a uma velocidade constante de 18 m/s. Quando calcula que é oportuno, a Mulher Maravilha se lança da ponte e pousa com grande precisão 10,0 m abaixo, bem no teto do caminhão. Calcule a que distância o caminhão estava da ponte quando saltou, nos seguintes casos:
a) Se ela começou com velocidade inicial zero.
b) Ela começou a descer verticalmente com uma velocidade inicial de 2 m/s.

Solução
Para resolver o exercício é necessário levar em conta que existem dois objetos em movimento. O primeiro é o caminhão, com movimento retilíneo uniforme no sentido horizontal, e o segundo é a mulher maravilha, cujo movimento é acelerado no sentido vertical.
Para que a Mulher Maravilha pouse com segurança na plataforma do caminhão, o tempo que o caminhão leva para percorrer a distância $latex \Delta x$ que o separa da ponte deve ser igual ao tempo que ela leva para cair os 10 m de altura.
Esse tempo é o seguinte:
$$y=\frac{1}{2}gt^2\Rightarrow t=\sqrt{\frac{2y}{g}}$$
$$t=\sqrt{\frac{2\times 10\hspace{1mm}m}{9,8\hspace{1mm}\dfrac{m}{s^2}}}=1,43\hspace{1mm}s$$
Durante esse tempo, o caminhão, que está em movimento retilíneo uniforme, percorrerá essa distância:
$$\Delta x=18\hspace{1mm}\dfrac{m}{s}\times1,43\hspace{1mm}s= 25,74\hspace{1mm}m$$
E a resposta é que o caminhão estava a 25,74 metros da ponte quando a Mulher Maravilha saltou dela.
b) Se a Mulher Maravilha começar com uma determinada velocidade inicial, o tempo necessário para cair 10 metros será menor. Nos cálculos a seguir, por conveniência, a posição vertical para baixo é considerada positiva:
$$y=v_0t+\frac{1}{2}gt^2$$
$$10=2t+4,9t^2$$
$$4,9t^2+2t-10=0$$
Cuja solução é:
$$t=1,24\hspace{1mm}s$$
Nesse caso, o caminhão deve estar na distância seguinte, também mais curta do que no caso anterior:
$$\Delta x=18\hspace{1mm}\dfrac{m}{s}\times1,24\hspace{1mm}s= 22,32\hspace{1mm}m$$
Lançamento vertical exercícios para resolver


Escreva a resposta na caixa de entrada.
Veja também
Interessado em aprender mais sobre movimento na física? Dê uma olhada nestas páginas:



