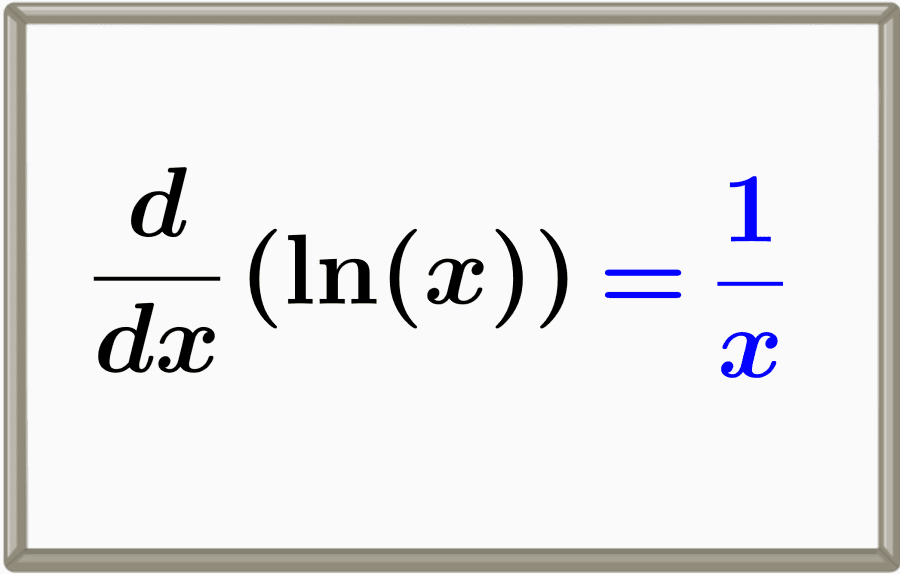O logaritmo natural, também chamado de ln(x), é o logaritmo de x na base e (número de Euler). A derivada do logaritmo natural é igual a um sobre x, 1/x. Podemos provar esta derivada usando limites ou derivação implícita.
Neste artigo, veremos como derivar a função logarítmica natural. Revisaremos alguns fundamentos, definições, fórmulas, comparações gráficas de ln(x) e sua derivada, provas e alguns exemplos.
Prova da derivada do logaritmo natural de x
Prova da derivada de ln(x) usando limites
Antes de aprender a prova da derivada da função logarítmica natural, é recomendado aprender/revisar o primeiro princípio dos limites, o número de Euler e a regra de L’hopital como pré-requisitos.
Para revisar, qualquer função pode ser diferenciada definindo-a igual ao limite de
$$ \frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$$
Suponha que nos peçam para encontrar a derivada de
$$ f(x) = \ln{(x)}$$
então temos
$$ \frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \ln{(x+h)} – \ln{(x)} }{h}}$$
Com esta equação ainda não é possível expressar o limite devido ao denominador h onde se for substituído por zero, permanecerá indefinido. Portanto, podemos verificar se a aplicação de algumas propriedades dos logaritmos pode ser útil.
A propriedade de divisão de logaritmos afirma que o logaritmo de um quociente é a diferença dos logaritmos. Podemos ver que o numerador satisfaz esta condição. Aplicando isso, temos
$$ \frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \ln{(x+h)} – \ln{(x)} }{h}}$$
$$ \frac{d}{dx} f(x) = \lim \limits_{h \to 0} { \frac{ \ln{\left(\frac{x+h}{x} \right)} }{h}}$$
$$ \frac{d}{dx} f(x) = \lim \limits_{h \to 0} { \ln{\left(\frac{x+h}{x} \right)} \cdot \frac{1}{h}}$$
Reorganizando, temos
$$ \frac{d}{dx} f(x) = \lim \limits_{h \to 0} { \frac{1}{h} \cdot \ln{\left(\frac{x+h}{x} \right)} }$$
$$ \frac{d}{dx} f(x) = \lim \limits_{h \to 0} { \frac{1}{h} \cdot \ln{\left(1 + \frac{h}{x} \right)} }$$
Podemos tentar eliminar o denominador h substituindo
$$ h = vx $$
onde
$$ v = \frac{h}{x} $$
o que prova algebricamente que quando h se aproxima de 0, v também se aproxima de 0.
Substituindo, temos
$$ \frac{d}{dx} f(x) = \lim \limits_{v \to 0} { \frac{1}{vx} \cdot \ln{\left(1 + v \right)} }$$
Reorganizando, temos
$$ \frac{d}{dx} f(x) = \lim \limits_{v \to 0} { \frac{1}{x} \cdot \frac{1}{v} \ln{\left(1 + v \right)} }$$
Agora podemos avaliar o limite de \(\frac{1}{x}\) quando v se aproxima de 0
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { \frac{1}{v} \ln{\left(1 + v \right)} }$$
Aplicando a propriedade do poder dos logaritmos ao nosso limite restante, temos
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { \left( \ln{\left(1 + v \right)} \right)^{\frac{1}{v}} }$$
Como você notará, o logaritmo natural que temos no limite restante é agora exatamente a definição matemática do número de Euler e.
Se
$$ (1 + v)^{\frac{1}{v}} = e $$
com base na definição do número de Euler, então
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} {\ln{(e)}}$$
Avaliando ln(e), sabemos que é igual a um. Portanto, temos
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} {(1)}$$
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot (1)$$
Portanto, a derivada do logaritmo natural na forma de \(\ln{(x)}\) é:
$$ \frac{d}{dx} (\ln{(x)}) = \frac{1}{x}$$
Alternativamente, em vez da definição do número de Euler, também podemos avaliar o mesmo limite restante aplicando a regra de L’hopital.
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { \frac{1}{v} \ln{\left(1 + v \right)} }$$
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { \frac{\ln{\left(1 + v \right)}}{v} }$$
Este limite restante satisfaz a condição \(\frac{0}{0}\). Avaliando temos
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { \frac{\ln{\left(1 + v \right)}}{v} }$$
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { \frac{ \frac{1}{1+v} }{1} }$$
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { \frac{1}{1+v} }$$
Avaliando substituindo o valor de aproximação de v, temos
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { \frac{1}{1+(0)} }$$
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { \frac{1}{1} }$$
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot \lim \limits_{v \to 0} { 1 }$$
$$ \frac{d}{dx} f(x) = \frac{1}{x} \cdot (1)$$
$$ \frac{d}{dx} (\ln{(x)}) = \frac{1}{x}$$
Prova da derivada de ln(x) usando diferenciação implícita
Nesta demonstração, você é incentivado a aprender/revisar derivadas de funções exponenciais e diferenciação implícita.
Suponha que temos a equação
$$ y = \ln{(x)}$$
Na forma logarítmica geral, é
$$ \log_{e}{x} = y$$
E na forma exponencial é
$$ e^y = x$$
Diferenciando implicitamente a forma exponencial em termos de x, temos
$$ e^y = x$$
$$ \frac{d}{dx} (e^y) = \frac{d}{dx} (x) $$
$$ e^y \cdot \frac{dy}{dx} = 1 $$
Isolando \(\frac{dy}{dx}\), temos
$$ \frac{dy}{dx} = \frac{1}{e^y} $$
Lembre-se disso, \(y = \ln{(x)}\). Substituindo isso no y da nossa derivada, temos
$$ \frac{dy}{dx} = \frac{1}{e^{(\ln{(x)})}} $$
Avaliando, agora temos a derivada de \(y = \ln{(x)}\)
$$ y’ = \frac{1}{x} $$
Gráfico de ln(x) vs. sua derivada
Dada a função
$$ f(x) = \ln{(x)}$$
seu gráfico é
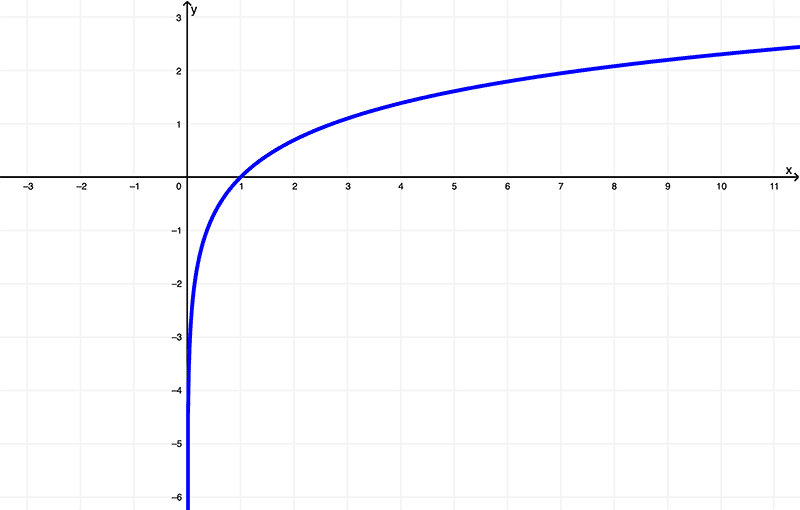
E como já sabemos, diferenciando \(f(x) = \ln{(x)}\), obtemos
$$ f'(x) = \frac{1}{x}$$
que é ilustrado graficamente como
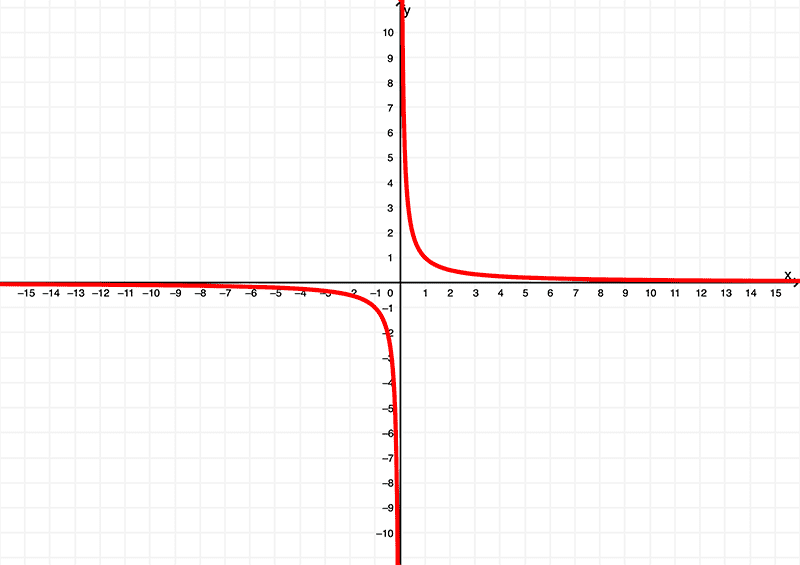
Comparando os dois gráficos em um, temos
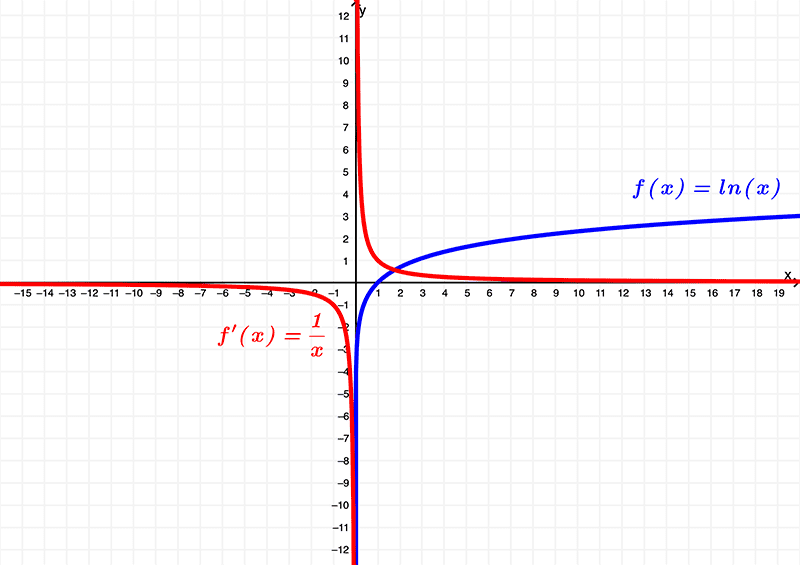
Usando seus gráficos, pode-se ver que a função original (f(x) = \ln{(x)}) tem um domínio de
\( (0,\infty) \) ou \( x | x > 0 \)
e existe dentro da imagem de
\( (-\infty, \infty) \) ou todos os números reais
enquanto a derivada \(f'(x) = \frac{1}{x} \) tem domínio de
\( (-\infty,0) \cup (0,\infty) \) ou \( x | x \neq 0 \)
e existe dentro da imagem de
\( (-\infty,0) \cup (0,\infty) \) ou \( y | y \neq 0 \)
Exemplos
Os exemplos seguintes mostram como derivar uma função logarítmica natural composta.
EXEMPLO 1
Encontre a derivada de $latex f(x) = \ln(4x)$
Solução
Esta é uma função logarítmica natural composta, pelo que podemos utilizar a regra da cadeia para a derivar.
Considerando $latex u=4x$ como a função interna, podemos escrever $latex f(u)=\ln(u)$. Assim, usando a regra da cadeia, temos:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=\frac{1}{u} \times 4$$
Substituindo $latex u=4x$ de volta à função, temos:
$$\frac{dy}{dx}=\frac{4}{4x}$$
EXEMPLO 2
Determine a derivada de $latex F(x) = \ln(4x^2-6x)$.
Solução
Vamos usar a regra da cadeia. Portanto, consideramos $latex u=4x^2-6x$ como a função interna e $latex f(u)=\ln(u)$ como a função externa.
Assim, começamos por encontrar a derivada da função externa:
$$\frac{d}{du} ( \ln(u) ) = \frac{1}{u}$$
Agora, encontramos a derivada da função interna, $latex g(x)$:
$$\frac{d}{dx}(g(x)) = \frac{d}{dx}(4x^2-6x)$$
$$\frac{d}{dx}(g(x)) = 8x-6$$
Multiplicamos a derivada da função interna pela derivada da função externa:
$$\frac{dy}{dx} = \frac{d}{du} (f(u)) \cdot \frac{d}{dx} (g(x))$$
$$\frac{dy}{dx} = \frac{1}{u} \cdot 8x-6$$
Finalmente, utilizamos a substituição $latex u=4x^2-6x$ e simplificamos:
$$\frac{dy}{dx} = \frac{1}{4x^2-6x} \cdot 8x-6$$
$$\frac{dy}{dx} = \frac{8x-6}{4x^2-6x}$$
$$\frac{dy}{dx} = \frac{4x-3}{2x^2-3x}$$
EXEMPLO 3
Qual é la derivada de $latex f(x) = \ln(\sin(x))$?
Solução
Neste caso, consideramos $latex u=\sin(x)$ como a função interna. Então $latex f(u)=\ln(u)$ é a função externa.
Usando a regra da cadeia, podemos escrever:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=\frac{1}{u} \times \cos(x)$$
Substituindo $latex u=\sin(x)$ de volta na função, temos:
$$\frac{dy}{dx}=\frac{1}{\sin(x)} \times \cos(x)$$
$$\frac{dy}{dx}=\frac{\cos(x)}{\sin(x)}$$
$$\frac{dy}{dx}=\cot(x)$$
Prática de derivadas de funções logarítmicas naturais
Veja também
Interessado em aprender mais sobre derivadas de funções logarítmicas? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
