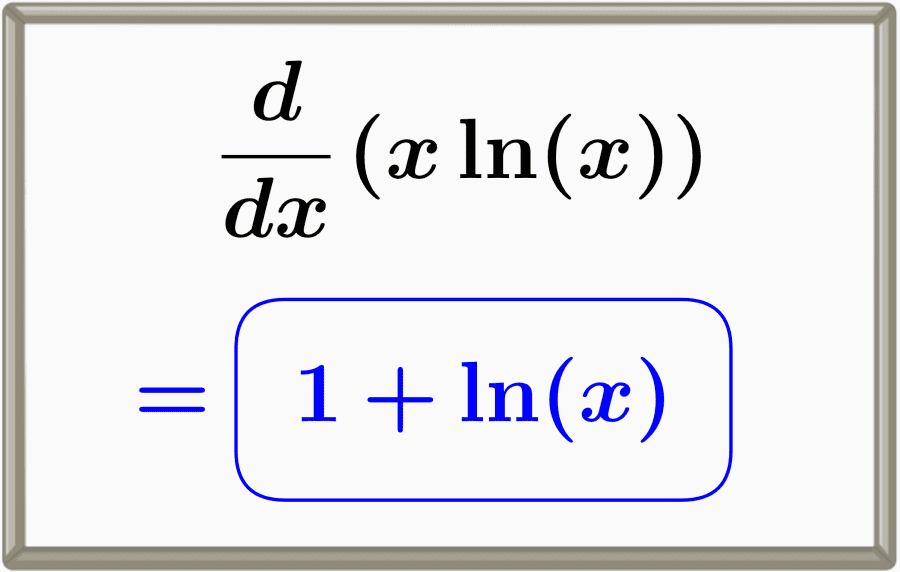A derivada de x ln(x) é igual a 1+ln(x). Essa derivada pode ser encontrada usando a regra do produto das derivadas.
Neste artigo veremos como obter a derivada de x ln(x). Revisaremos alguns princípios, comparações gráficas de derivados e não derivados x ln(x) e provas.
Provas da derivada do logaritmo natural, x ln(x)
As provas da derivada de \(x\ln{(x)}\) estão listadas abaixo. Essas provas também podem servir como os principais métodos para derivar essa função.
Prova da derivada de x ln(x) usando a fórmula da regra do produto
No processo de derivação de \(x\ln{(x)}\), a regra do produto é usada, pois o logaritmo natural de x é multiplicado por outro x. Aqui temos dois multiplicandos. São duas funções multiplicadas que não podemos simplificar algebricamente.
Você pode revisar a fórmula da regra do produto consultando este artigo: Regra do produto. Você também pode consultar este artigo para ver a prova da derivada do logaritmo natural usando limites: Derivada do logaritmo natural (ln(x)).
Temos a função
$$ f(x) = x\ln{(x)}$$
Podemos descobrir as duas funções que são multiplicadas. Há uma função logarítmica natural e um monômio neste caso. Definindo o primeiro multiplicando/termo como u, temos
$$ u = x$$
e definindo o segundo multiplicando/termo como v, temos
$$ v = \ln{(x)}$$
Lembre-se que a fórmula do produto derivado é
$$ \frac{d}{dx} uv = u \frac{d}{dx} v + v \frac{d}{dx} u$$
Ou seja, a função u vezes v é obtida pela multiplicação de u pela derivada de v e depois pela adição de v vezes a derivada de u. Aplicando esta fórmula à nossa função dada, temos
$$ \frac{d}{dx} uv = (x) \frac{d}{dx} (\ln{(x)}) + (\ln{(x)}) \frac{d}{dx} (x)$$
Avaliando a derivada de u usando a regra da potência e v usando a derivada do logaritmo natural, temos
$$ \frac{d}{dx} uv = (x) \cdot \left(\frac{1}{x} \right) + (\ln{(x)}) \cdot (1)$$
Simplificando, temos
$$ \frac{d}{dx} uv = \frac{x}{x} + (\ln{(x)}) $$
$$ \frac{d}{dx} uv = 1 + (\ln{(x)}) $$
Como resultado, chegamos à fórmula derivada \(x\ln{(x)}\).
$$ \frac{d}{dx} x\ln{(x)} = 1 + (\ln{(x)}) $$
Prova da derivada de x ln(x) usando diferenciação implícita
Aprender/revisar derivadas de funções exponenciais e diferenciação implícita é recomendado para esta demonstração.
Temos a função
$$ y = x\ln{(x)}$$
Aplicando uma propriedade logarítmica, temos
$$ y = \ln{(x)^x}$$
$$ y = \ln{\left(x^x\right)}$$
Na forma logarítmica geral, temos
$$ \log_{e}{x^x} = y$$
E na forma exponencial, temos
$$ e^y = x^x$$
Diferenciando implicitamente a forma exponencial em termos de x, temos
$$ e^y = x^x$$
$$ e^y \cdot \frac{d}{dx} = \frac{d}{dx} (x^x) $$
$$ e^y \cdot \frac{d}{dx} = \frac{d}{dx} (x^x + x^x \ln{(x)}) $$
Resolvendo para \( \frac{dy}{dx} \), temos
$$ \frac{dy}{dx} = \frac{x^x + x^x \ln{(x)}}{e^y} $$
Lembramos que no início, \( y = x\ln{(x)} \) ou \( y = \ln{\left(x^x\right)} \). Substituindo isso no y da nossa derivada, temos
$$ \frac{dy}{dx} = \frac{x^x + x^x \ln{(x)}}{e^{\left(\ln{\left(x^x\right)}\right)}} $$
Simplificando e aplicando uma propriedade logarítmica, temos
$$ \frac{dy}{dx} = \frac{x^x + x^x \ln{(x)}}{x^x} $$
$$ \frac{dy}{dx} = \frac{x^x}{x^x} + \frac{x^x \ln{(x)}}{x^x} $$
$$ \frac{dy}{dx} = 1 + \ln{(x)} $$
Avaliando, agora temos a derivada de \( y = x\ln{(x)} \)
$$ y’ = 1 + \ln{(x)} $$
Gráfico de x ln(x) vs. sua derivada
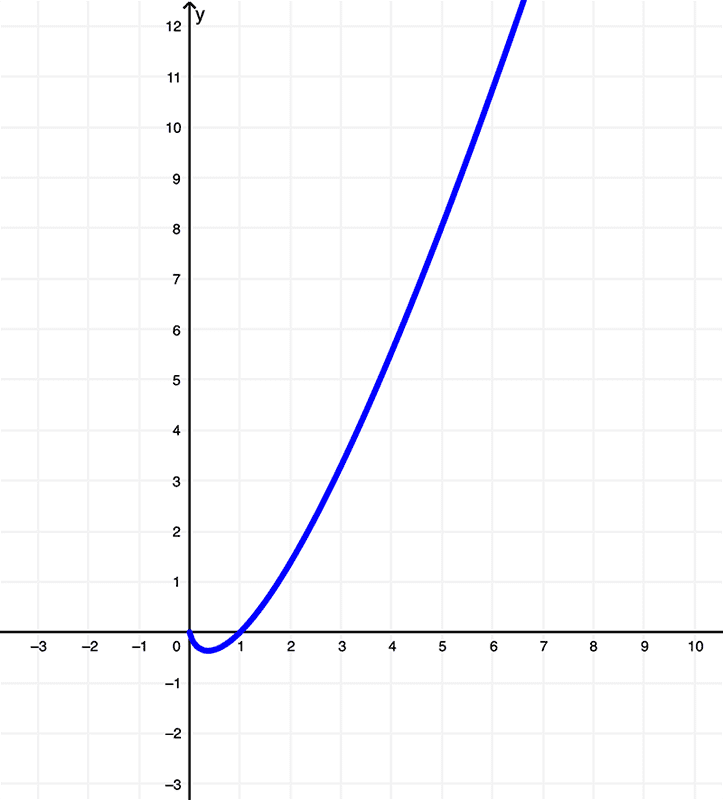
Temos a função
$$ f(x) = x\ln{(x)}$$
e seu gráfico é
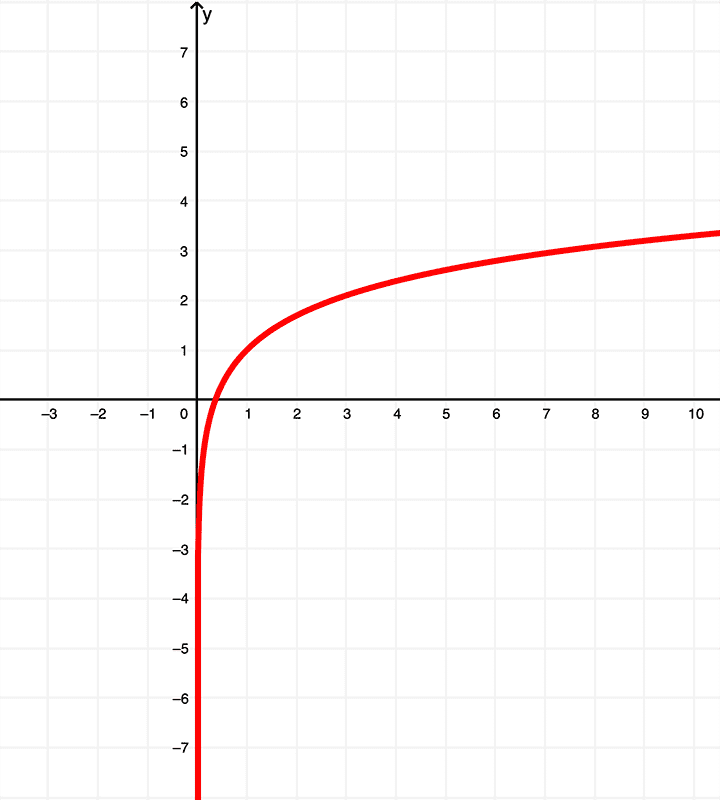
E como aprendemos anteriormente, derivando \(f(x) = x\ln{(x)}\), temos
$$ f'(x) = 1 + \ln{(x)}$$
que é ilustrado graficamente como
Ilustrando os dois gráficos em um, temos
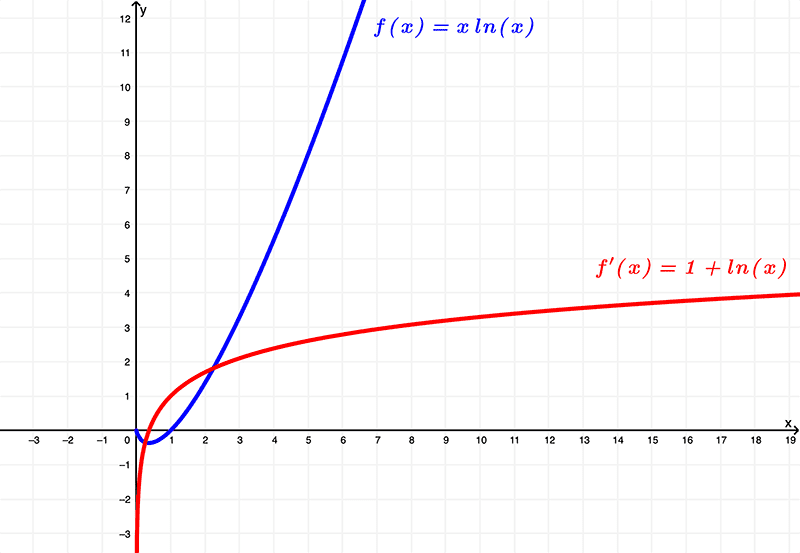
Examinando as diferenças entre essas funções usando esses gráficos, vemos que a função original \(f(x) = x\ln{(x)}\) tem um domínio de
\( (0,\infty) \) ou \( x | x > 0 \)
e está dentro da imagem de
\( \left[-\frac{1}{e}, \infty \right) \) ou \( y | y \geq -\frac{1}{e} \)
enquanto a derivada \(f'(x) = 1 + \ln{(x)}\) tem um domínio de
\( (0,\infty) \) ou \( x | x > 0 \)
que está dentro da imagem de
\( (-\infty,\infty) \) ou todos os números reais
Veja também
Interessado em aprender mais sobre derivadas de funções logarítmicas? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
