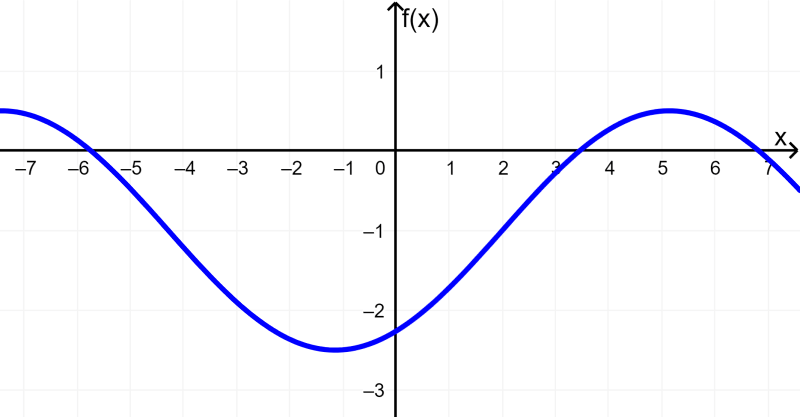
Existem várias transformações de funções trigonométricas com as quais podemos mudar para os gráficos das funções trigonométricas padrão. Podemos fazer mudanças na amplitude, no período, na fase da função. Também podemos realizar traduções verticais e produzir reflexos a partir dos gráficos.
A seguir, veremos essas transformações de funções trigonométricas em detalhes, juntamente com alguns exemplos para visualizar o efeito das transformações.
ALGEBRA
Relevante para…
Aprender a realizar transformações de funções trigonométricas.
ALGEBRA
Relevante para…
Aprender a realizar transformações de funções trigonométricas.
Amplitude de funções trigonométricas
A amplitude de uma função trigonométrica é o deslocamento máximo no gráfico dessa função. A amplitude é a distância do valor médio da curva até seu valor máximo ou mínimo.
No caso das funções seno e cosseno, a amplitude é o valor do coeficiente líder da função. Podemos alterar a amplitude dessas funções multiplicando a função por uma constante A. Por exemplo, se a função for $latex y= A \sin(x)$, então a amplitude é |A|.
No caso das funções tangente, cossecante, secante e cotangente, a amplitude será infinitamente grande, independentemente do valor de A.
Período de funções trigonométricas
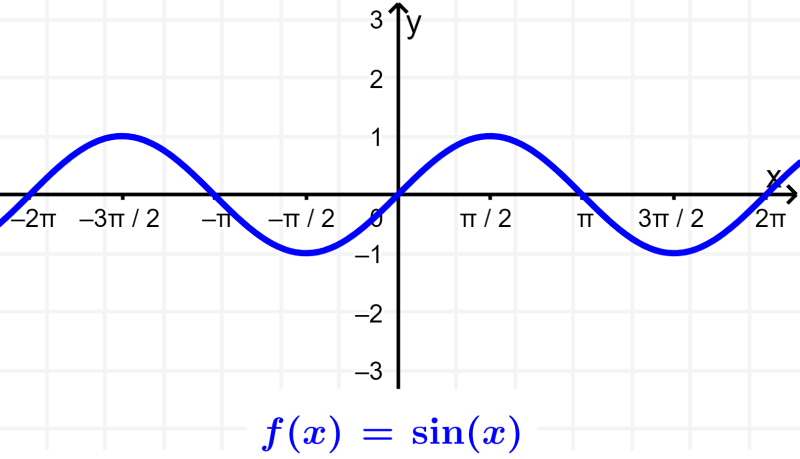
O período de uma função trigonométrica é a duração de um ciclo. Ou seja, o período é o deslocamento de x em que o gráfico da função começa a se repetir. Por exemplo, considere a função $latex y= \sin(x)$:
O valor $latex x=2 \pi$ é o ponto em que o gráfico começa a se repetir.
O coeficiente de x é a constante que determina o período. A forma geral é $latex y=\sin(Bx)$, onde B determina o período. Para as funções seno, cosseno, secante e cossecante, o período é $latex 2 \pi$ e podemos alterar o período de acordo com a fórmula:
$latex \text{período}=\frac{\text{período original}}{|B|}$
Quando |B| for maior que 1, o novo período é menor que o original, então a função parece ter compressão horizontal. Quando |B| for menor que 1, a função parece ter um alongamento horizontal.
As funções tangente e cotangente têm um período de $latex \pi$.
Fase de funções trigonométricas
A fase de uma função trigonométrica refere-se à translação horizontal à direita do gráfico da função.
A forma geral da função trigonométrica é $latex y=A \sin B(x-C)$, onde A é a amplitude, B é o período e C é a fase.
O gráfico de $latex y=\sin(x)$ pode ser traduzido para a direita ou esquerda. Se C for positivo, a tradução é para a direita e se C for negativa, a tradução é para a esquerda.
Movimento vertical
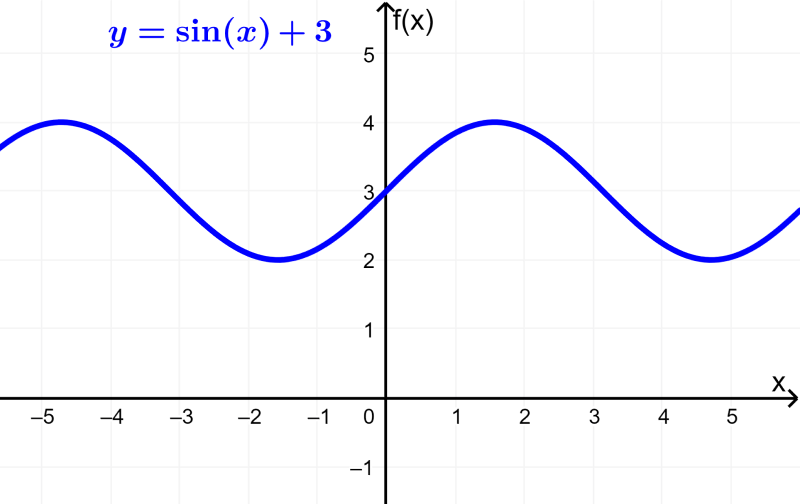
Ao adicionar um valor D à função trigonométrica, traduziremos seu gráfico verticalmente. Se D for positivo, o gráfico se moverá para cima por um fator de D, e se D for negativo, o gráfico se moverá para baixo.
A forma geral da função seno com translação vertical é $latex y=A \sin B(x-C)+D$.
Reflexões
Para obter o gráfico de:
- $latex y=-f(x)$ refletimos o gráfico de $latex y=f(x)$ em relação ao eixo x
- $latex y=f(-x)$ refletimos o gráfico de $latex y=f(x)$ em relação ao eixo y
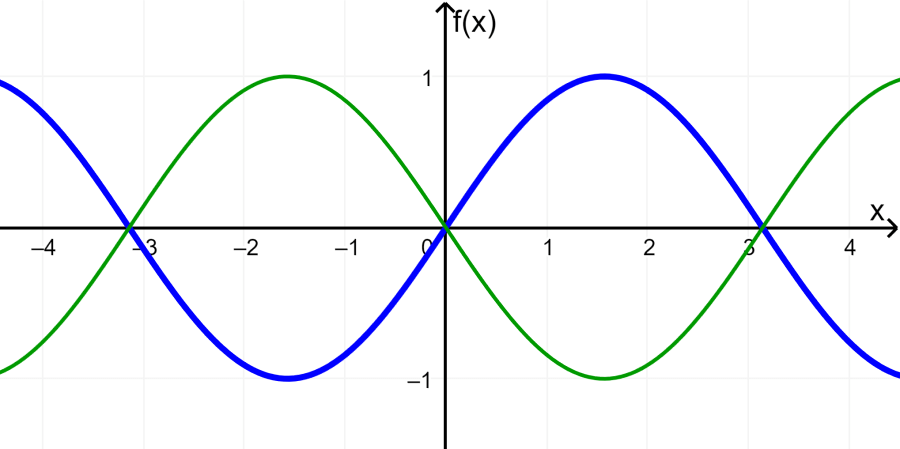
O gráfico a seguir mostra a função seno em azul, ou seja, a função $latex y=\sin(x)$. A função em verde representa a função $latex y=-f(x)$ e a função $latex y=f(-x)$. Neste caso particular, a reflexão em x da função é igual à reflexão em y.
Exemplos de funções trigonométricas com transformações
EXEMPLO 1
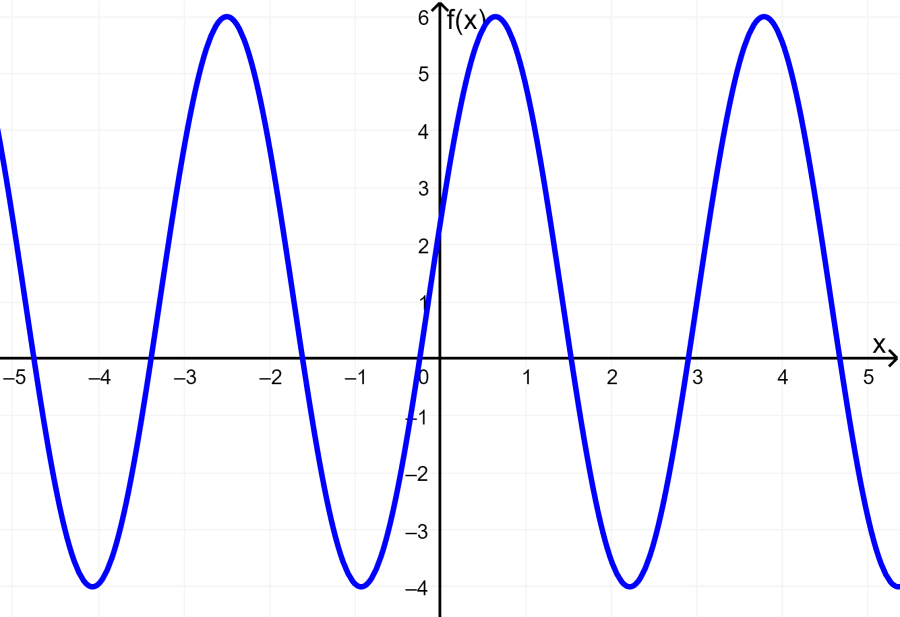
A seguir está o gráfico da função $latex y=5 \sin(2(x-3))+1$.
Aqui, temos:
- Amplitude: $latex A=5$
- Período: $latex \text{periodo}=\frac{2\pi}{B}=\frac{2\pi}{2}=\pi$
- Fase: $latex C=3$
- Movimento vertical: $latex D=1$
EXEMPLO 2
A seguir está o gráfico da função $latex y=1,5 \sin(0,5(x-2)) -1$.
Esta função tem o seguinte:
- Amplitude: $latex A=1.5$
- Período: $latex \text{periodo}=\frac{2\pi}{B}=\frac{2\pi}{0.5}=4\pi$
- Fase: $latex C=2$
- Movimento vertical: $latex D=-1$
EXEMPLO 3
A seguir está o gráfico da função $latex y=3 \sin (2(x+3)) – 2$.
Nesta função, temos:
- Amplitude: $latex A=2$
- Período: $latex \text{periodo}=\frac{2\pi}{B}=\frac{2\pi}{2}=\pi$
- Fase: $latex C=-3$
- Movimento vertical: $latex D=-2$
Veja também
Você quer aprender mais sobre funções? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
