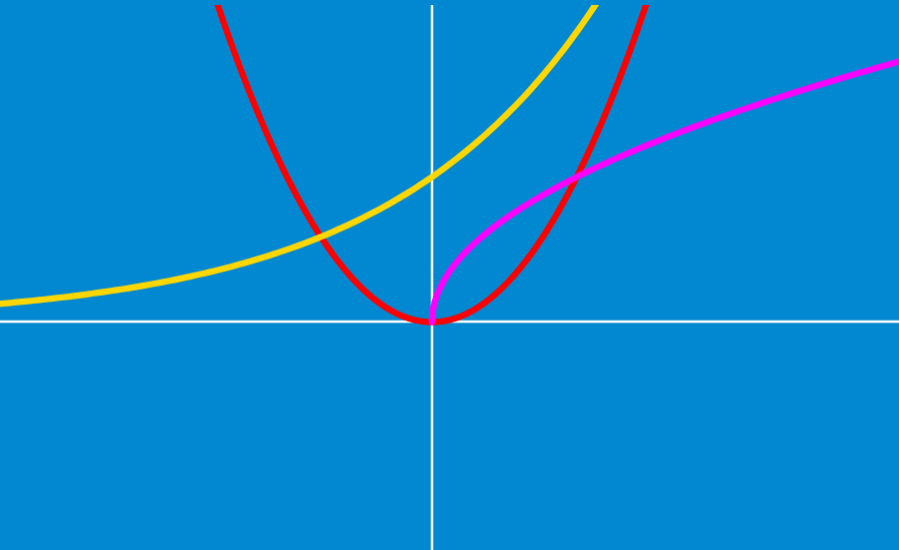
Existem vários tipos de funções algébricas que possuem características diferentes que as tornam únicas. Muitas dessas funções algébricas podem ser identificadas visualizando seu gráfico. Neste artigo, aprenderemos sobre os tipos de funções algébricas e seus gráficos, juntamente com algumas de suas características mais importantes.
O que são funções?
Uma função é uma relação entre um conjunto de entradas e um conjunto de saídas com a propriedade de que cada entrada está relacionada a exatamente uma saída. Suponha que temos os conjuntos P e Q, o mapeamento de P para Q será uma função apenas quando cada elemento no conjunto P tiver apenas um elemento do conjunto Q atribuído.
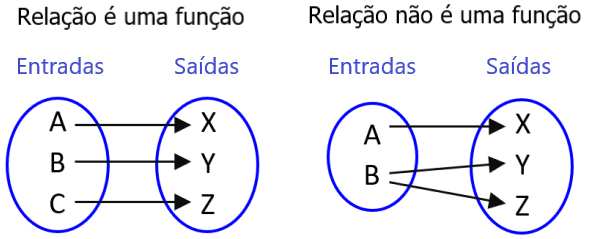
Condições para uma função
Os conjuntos P e Q não devem estar vazios.
Em uma função, uma determinada entrada é fornecida para obter uma determinada saída.
Uma função f: P → Q denota que f é uma função de P a Q, onde P é o domínio e Q é o intervalo.
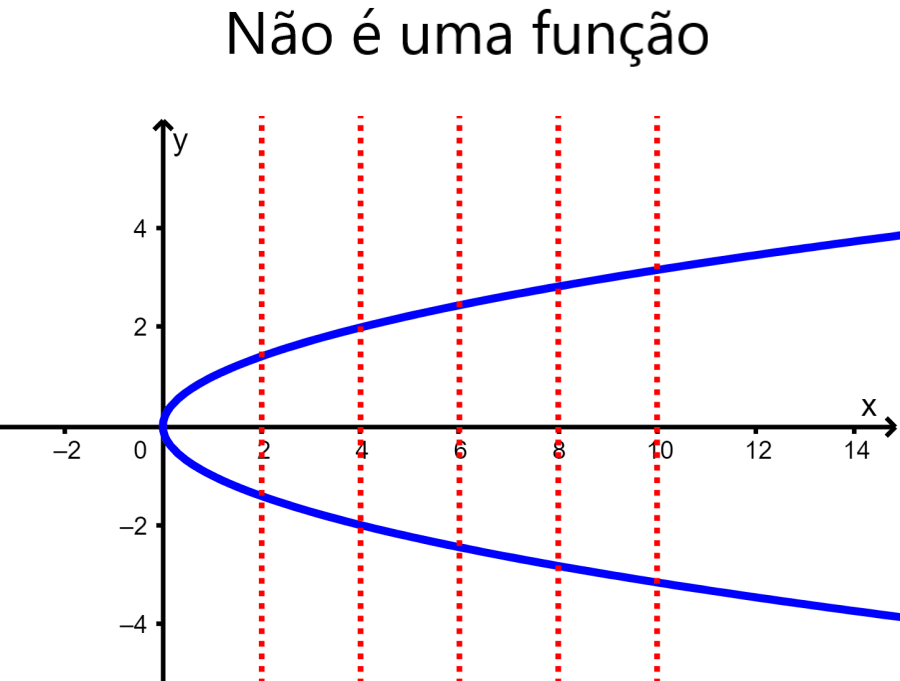
Teste de linha vertical: O teste de linha vertical é usado para determinar se a curva representa uma função ou não. Para que o gráfico seja uma função, qualquer linha vertical desenhada deve cruzar o gráfico em apenas um ponto. Se for possível traçar uma linha vertical que cruze o gráfico em dois ou mais de dois pontos, o gráfico não é uma função.
Representação de funções
As funções são geralmente representadas como $latex f(x)$.
Se tivermos a função $latex f(x)={{x}^3}$, lemos isso como f de x é igual a x ao cubo.
Lembre-se de que podemos usar qualquer letra do alfabeto em minúsculas ou maiúsculas para representar as funções e suas variáveis. Por exemplo, os itens a seguir também são representações válidas de funções:
$latex g(t), ~h(x), ~f(s)$
Quais são os tipos de funções algébricas?
A seguir estão os tipos mais importantes de funções algébricas:
- Função polinomial
- Função constante
- Função linear
- Função quadrática
- Função cúbica
- Função de identidade
- Função racional
- Função inversa
- Função exponencial
- Função logarítmica
- Funções trigonométricas
- Funções pares e ímpares
- Funções definidas por partes
- Função injetiva
- Função sobrejetiva
- Função bijetiva
- Função de valor absoluto
Tipos de funções algébricas e seus gráficos
Função polinomial
Uma função polinomial é uma função formada por um polinômio como
$latex f(x)=a{{x}^3}+b{{x}^2}+cx+d$
O domínio das funções polinomiais são todos os números reais. Essas funções são contínuas em todo o seu domínio.
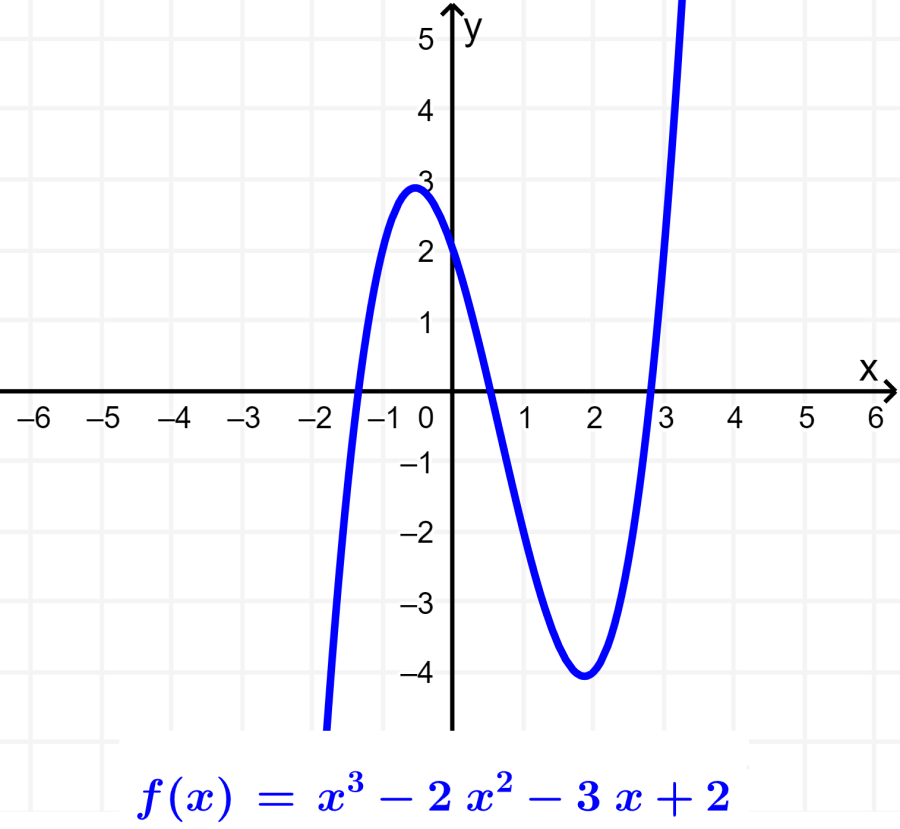
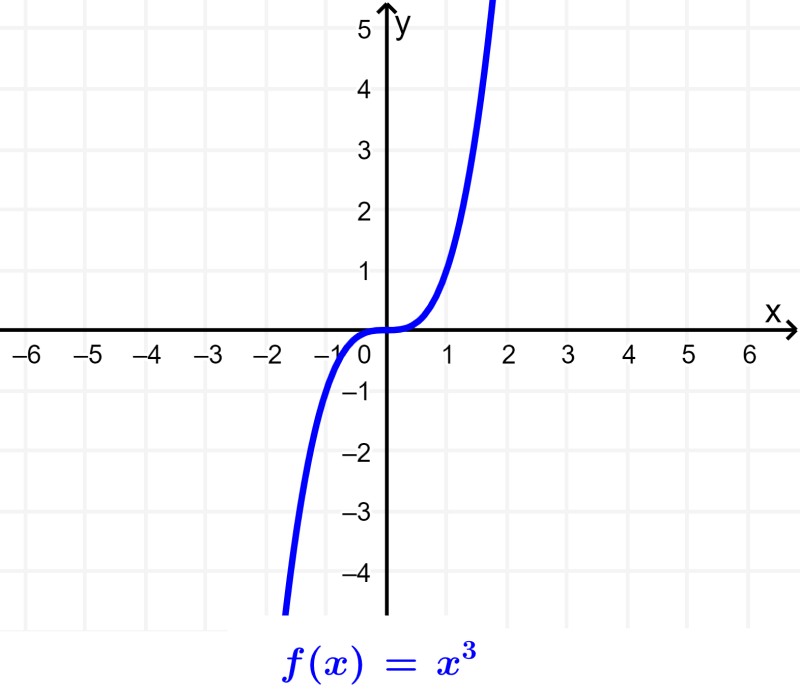
O maior poder na expressão é conhecido como o grau da função polinomial. Por exemplo, o gráfico a seguir representa uma função polinomial de terceiro grau:
Função contante
A função constante é uma função polinomial de grau zero, onde temos $latex f(x)=f(0)=c$. Não importa qual seja o valor de entrada, a função sempre retorna o mesmo valor constante.
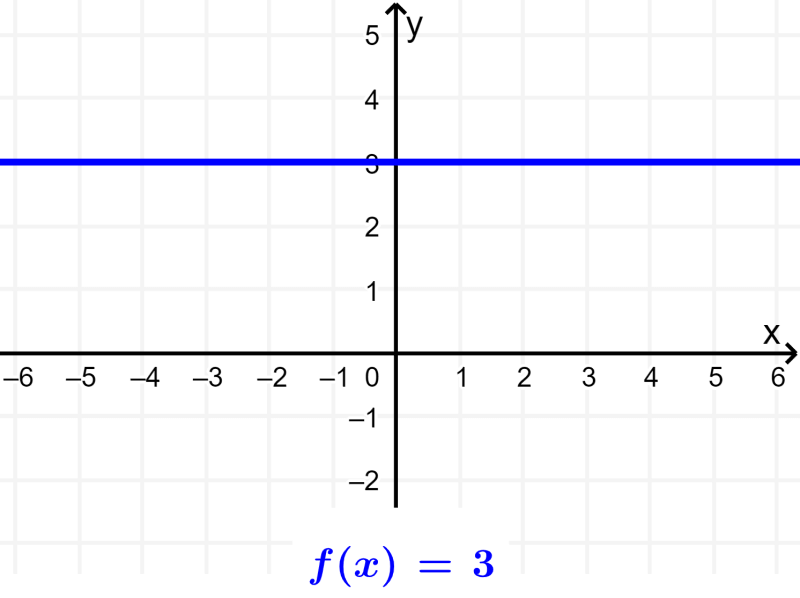
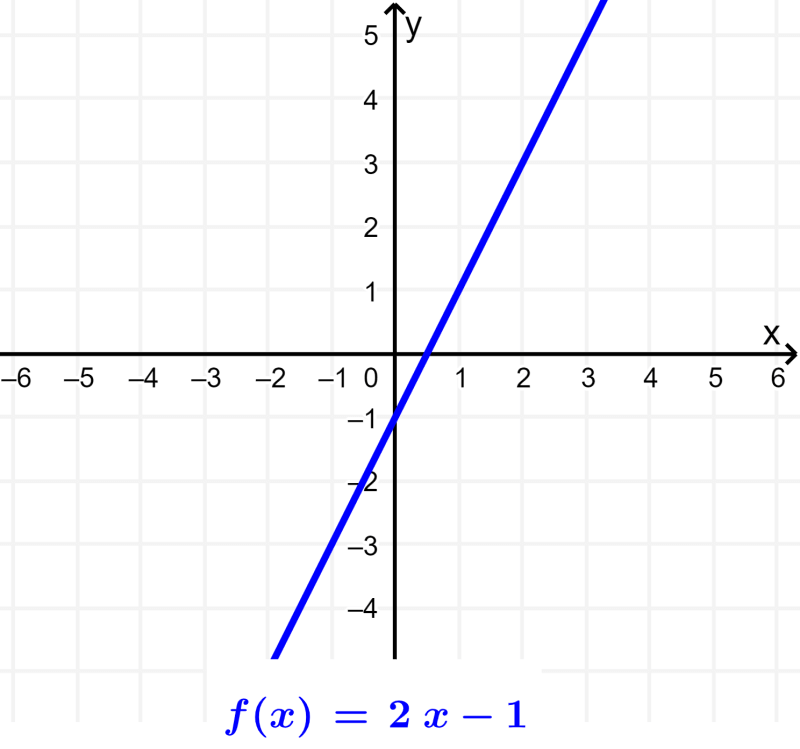
Função linear
Todas as funções da forma $latex f(x)=ax+b$, onde a e b são números reais e a é diferente de zero, são funções lineares. O gráfico dessas funções sempre será uma linha reta. Isso significa que a função linear é uma função polinomial de primeiro grau:
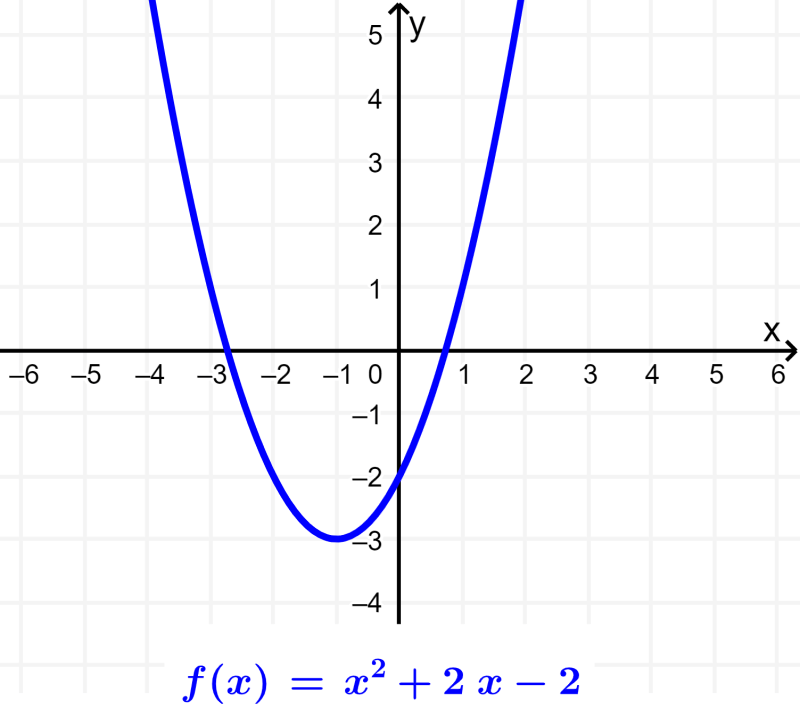
Função quadrática
Todas as funções que têm a forma $latex f(x)=a{{x}^2}+bx+c$, onde a, b e c são números reais e a é diferente de zero, são funções quadráticas. Uma função quadrática é uma função polinomial de segundo grau, então seu gráfico é uma parábola:
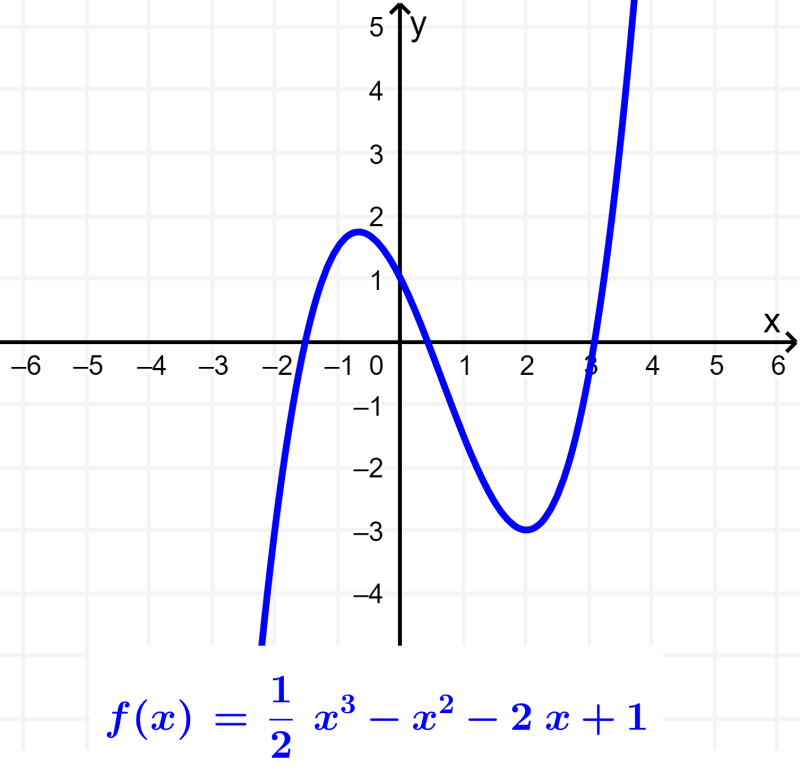
Função cúbica
Semelhante às funções polinomiais anteriores, a função cúbica tem a forma $latex f(x)=a{{x}^3}+b{{x}^2}+cx+d$, onde a, b, c e d são reais números e a é diferente de zero. Esta função é uma função polinomial de terceiro grau:
Função de identidade
Uma função de identidade é uma função em que a imagem de qualquer elemento é o mesmo elemento: $latex f(x)=x$.
A função de identidade é uma função linear com inclinação $latex m=1$ que passa pelo ponto (0, 0). Esta função divide o primeiro e o terceiro quadrantes em partes iguais:
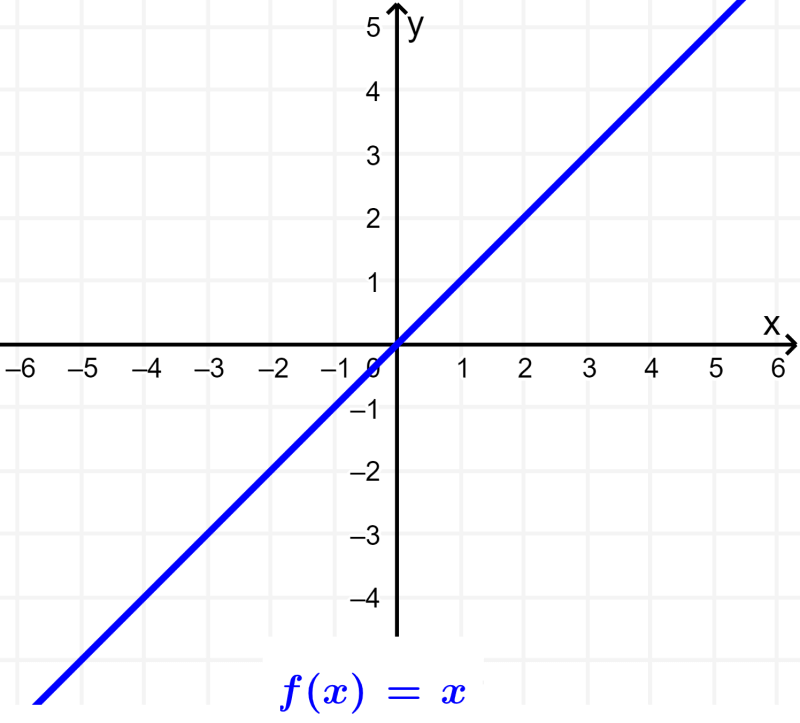
Função racional
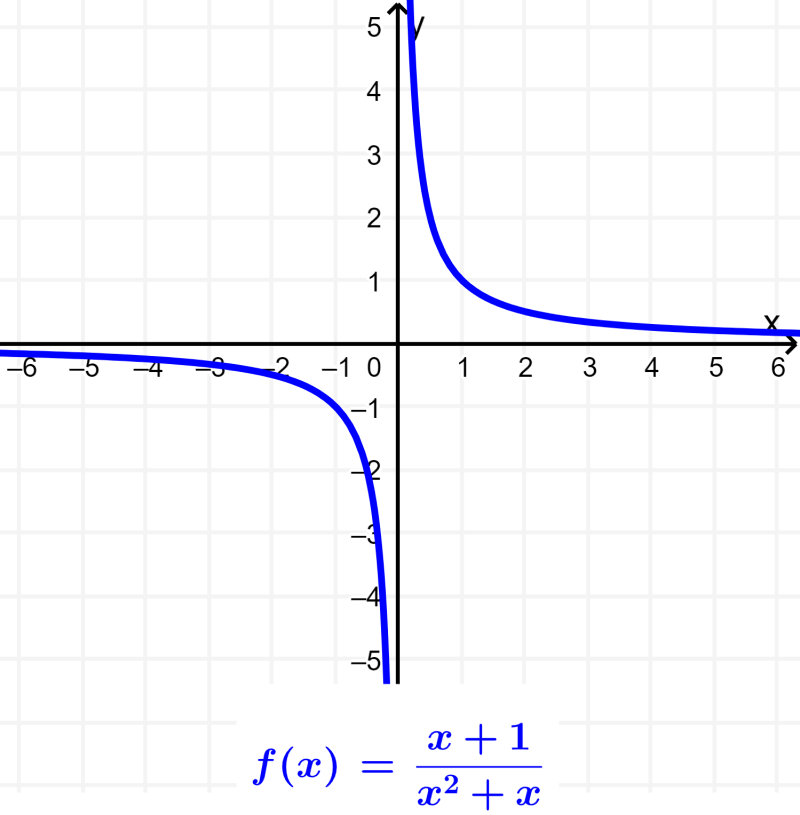
Funções racionais são funções representadas como frações de dois polinômios, $latex f(x)=\frac{{P(x)}}{{Q(x)}}$, onde o quociente é irredutível e $latex Q(x)$ é diferente de zero. O domínio de uma função racional são todos os números reais, exceto os números que tornam o denominador igual a zero.
Função inversa
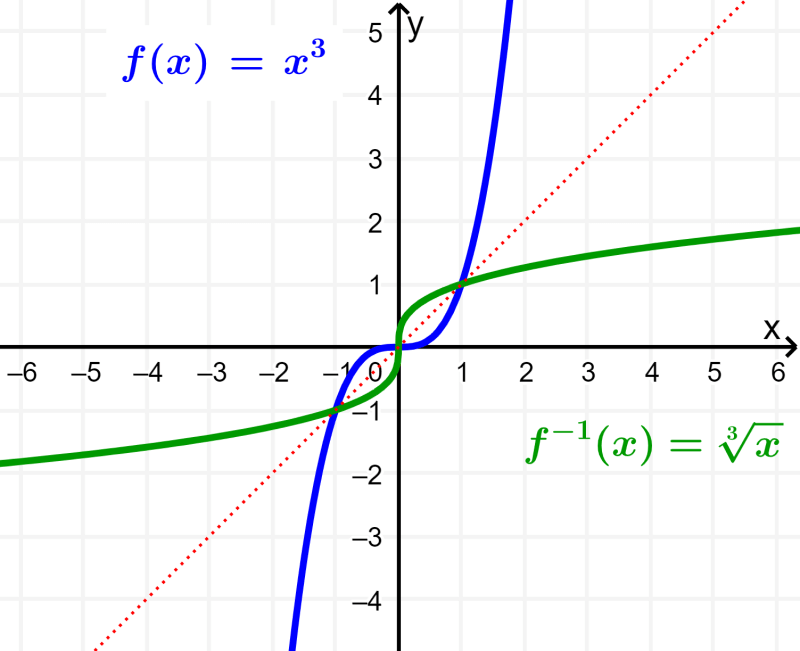
Uma função inversa é uma função que inverte o efeito da função original. Por exemplo, se a função original multiplica por 3, a função inversa divide por 3, e se a função original multiplica por 3 e adiciona 4, então a função inversa subtrai 4 e divide por 3. O seguinte é o gráfico do função $latex f(x)={{x}^3}$ e seu inverso:
Função exponencial
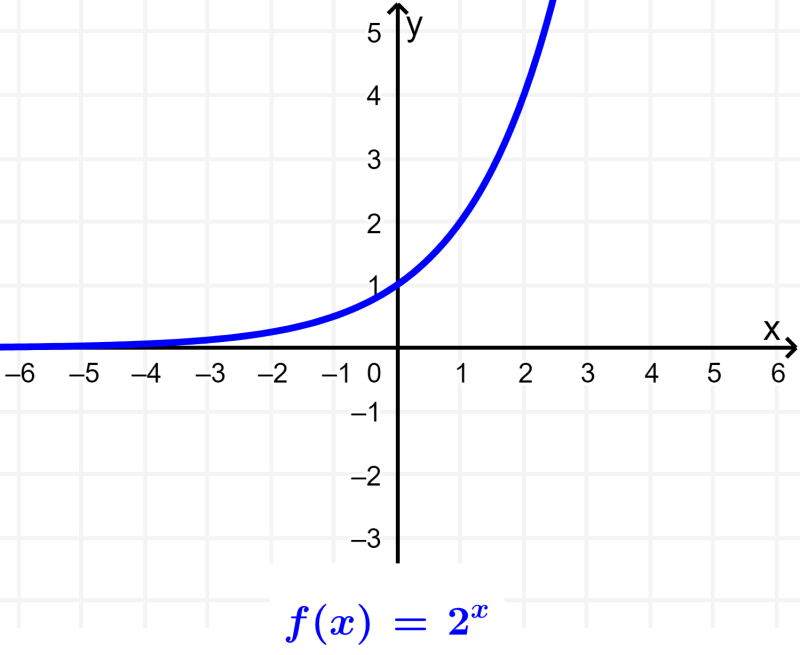
Funções exponenciais são funções que têm a variável como expoente de uma base. Essas funções têm a forma geral $latex f(x)={{b}^x}$, onde b é a base da função exponencial.
Função logarítmica
Uma função logarítmica é composta de um logaritmo com base b. Em sua forma mais simples, a função logarítmica tem a forma $latex f(x)=\log_{b}(x)$.
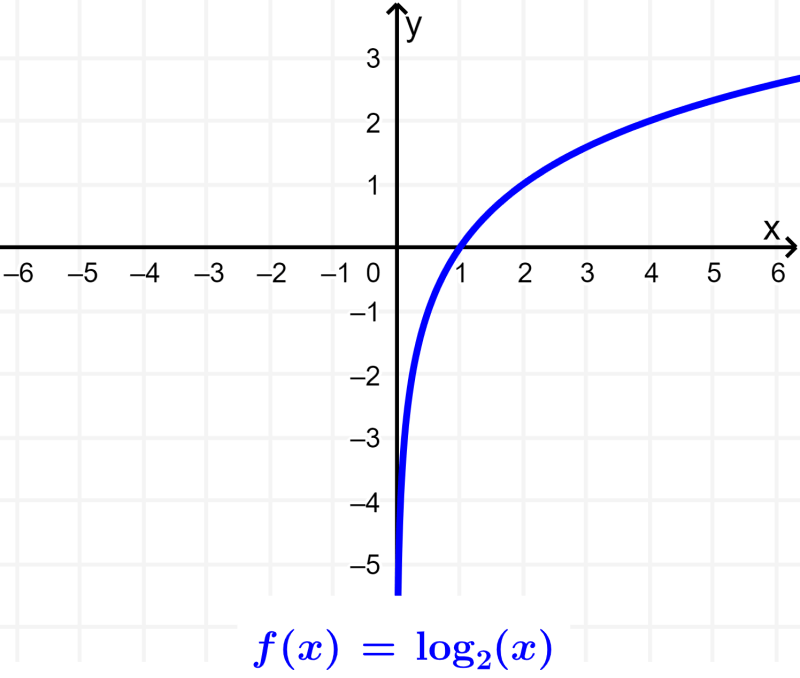
Funções trigonométricas
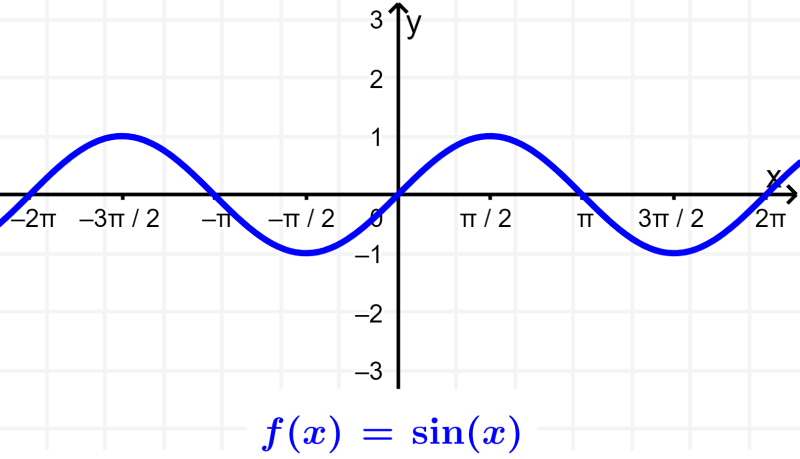
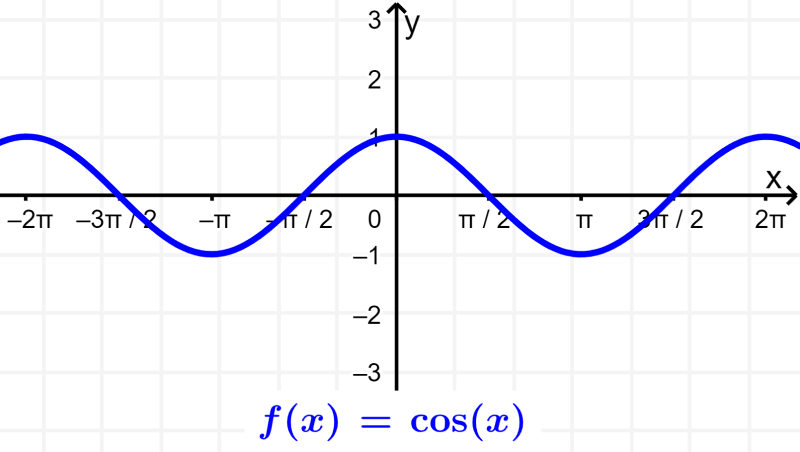
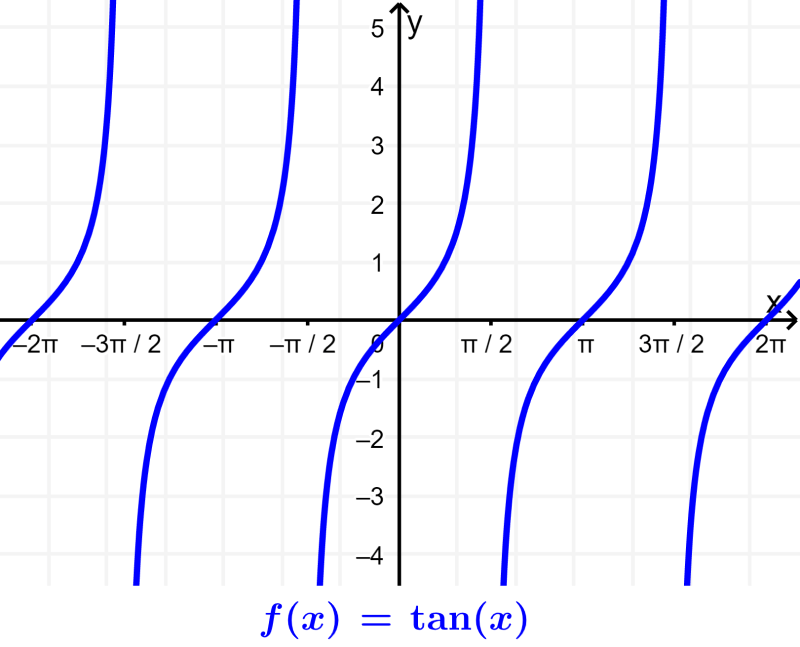
Funções trigonométricas são funções obtidas de diferentes relações dos três lados de um triângulo retângulo. As seis funções trigonométricas principais são seno, cosseno, tangente, cossecante, secante e cotangente.
Seno: O seno de um ângulo é definido como a razão entre o lado oposto (O) e a hipotenusa (H). $latex \sin(\theta)=\frac{O}{H}$.
Cosseno: O cosseno de um ângulo é definido como a razão entre o lado adjacente (O) e a hipotenusa (H). $latex \cos(\theta)=\frac{A}{H}$.
Tangente: A tangente de um ângulo é definida como a razão entre o lado oposto (O) e o lado adjacente (A). $latex \tan(\theta)=\frac{O}{A}$.
Cossecante: A cossecante é a razão trigonométrica recíproca do seno. A cossecante é definida como a razão entre a hipotenusa (H) e o lado oposto (H). $latex \csc(\theta)=\frac{H}{O}$.
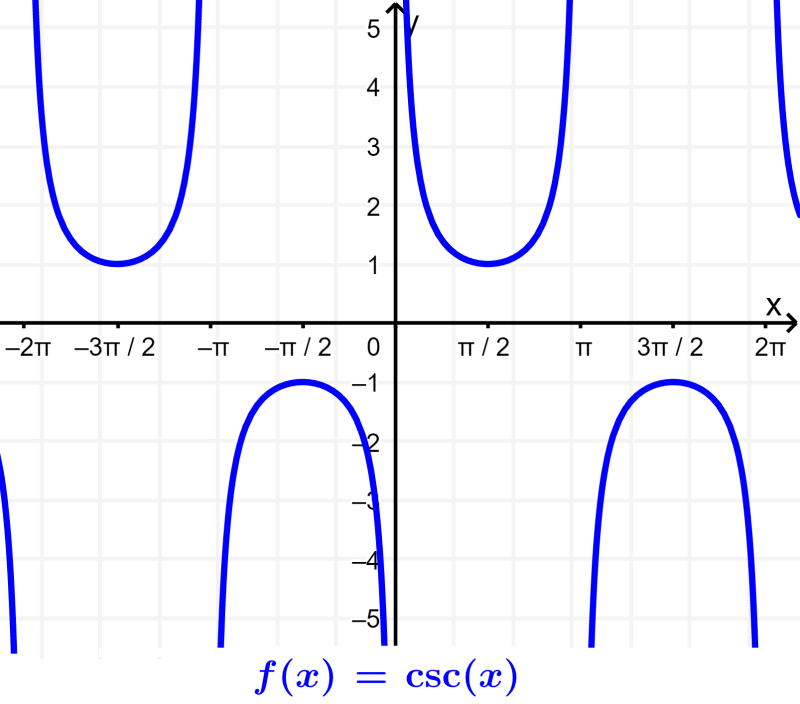
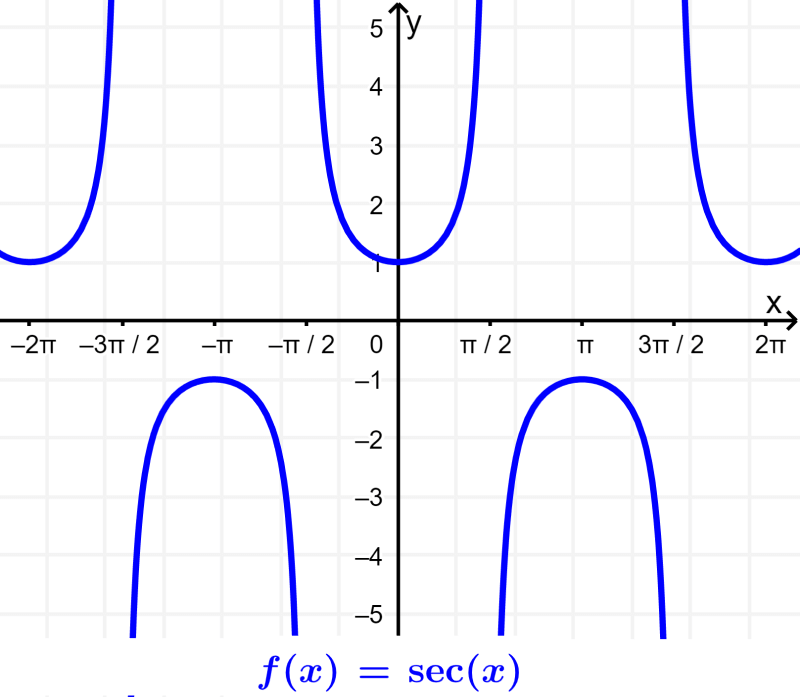
Secante: A secante é a razão trigonométrica recíproca do cosseno. A cossecante é definida como a razão entre a hipotenusa (H) e o lado adjacente. $latex \sec(\theta)=\frac{H}{A}$.
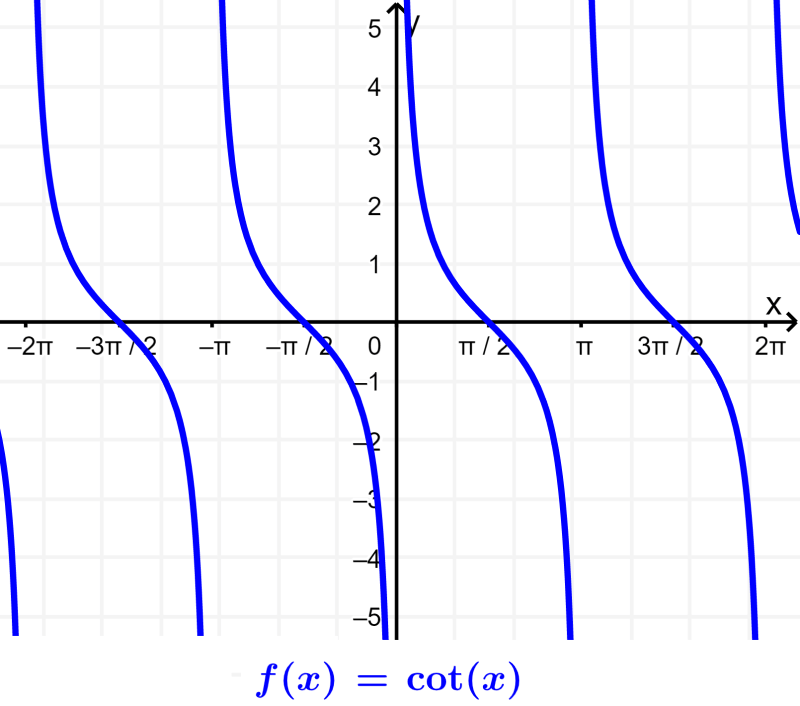
Cotangente: A cotangente é a razão trigonométrica recíproca da tangente. A cotangente é definida como a razão entre o lado adjacente e o lado oposto (O). $latex \cot(\theta)=\frac{A}{O}$.
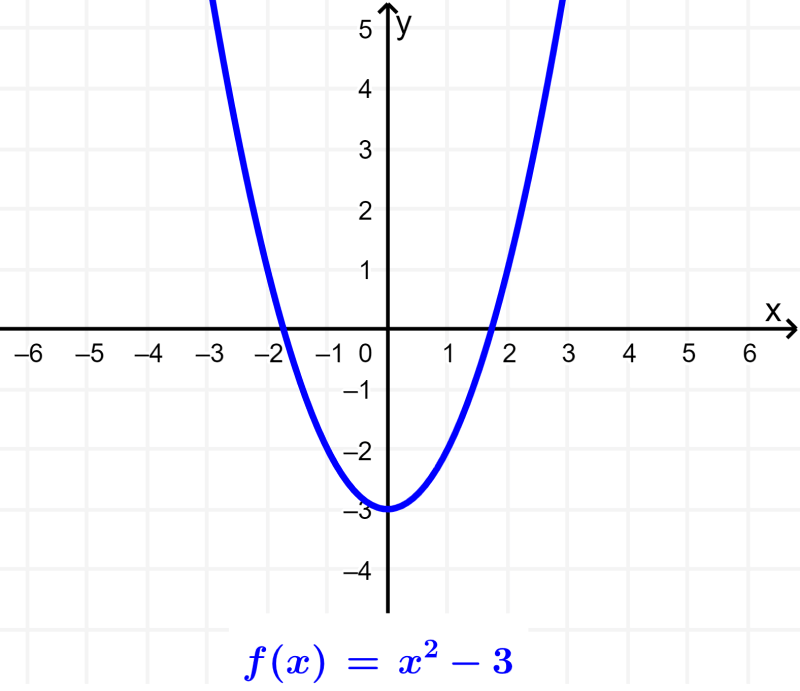
Funções pares e ímpares
Se tivermos que $latex f(x)=f(-x)$, então a função será par. A função par é simétrica em relação ao eixo y.
Se tivermos que $latex -f(x)=f(x)$, então a função será ímpar. A função ímpar é simétrica em relação à origem.
Funções definidas por partes
Funções definidas em partes ou também conhecidas como funções por partes, são funções que possuem expressões diferentes dependendo do intervalo em que a variável independente se encontra.
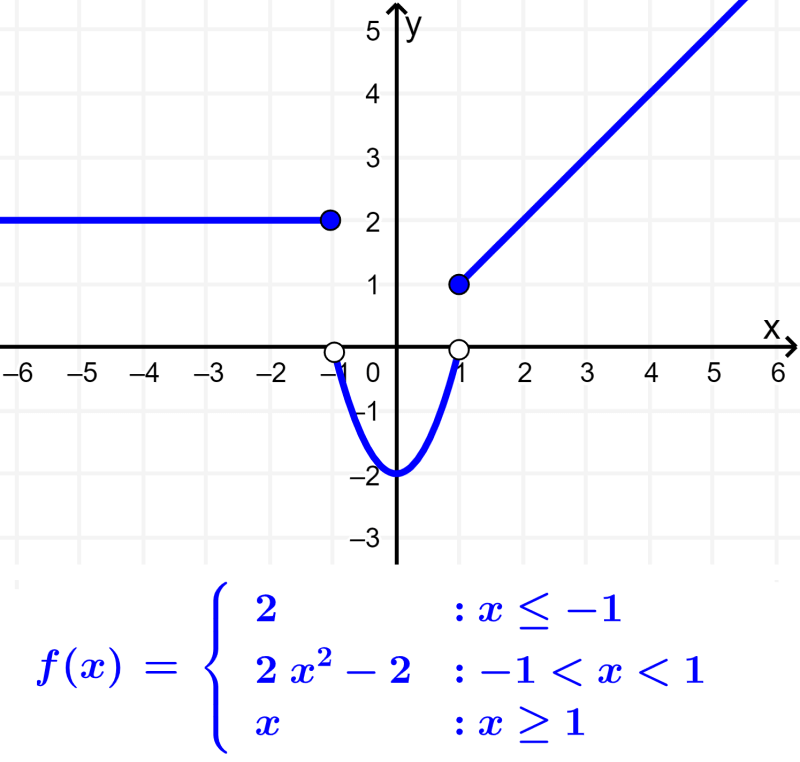
Função de valor absoluto
A função de valor absoluto faz com que as saídas da função sejam sempre positivas. Em sua forma mais simples, a função de valor absoluto tem a forma $latex f(x)=|x|$. Esta função forma um gráfico em forma de V.
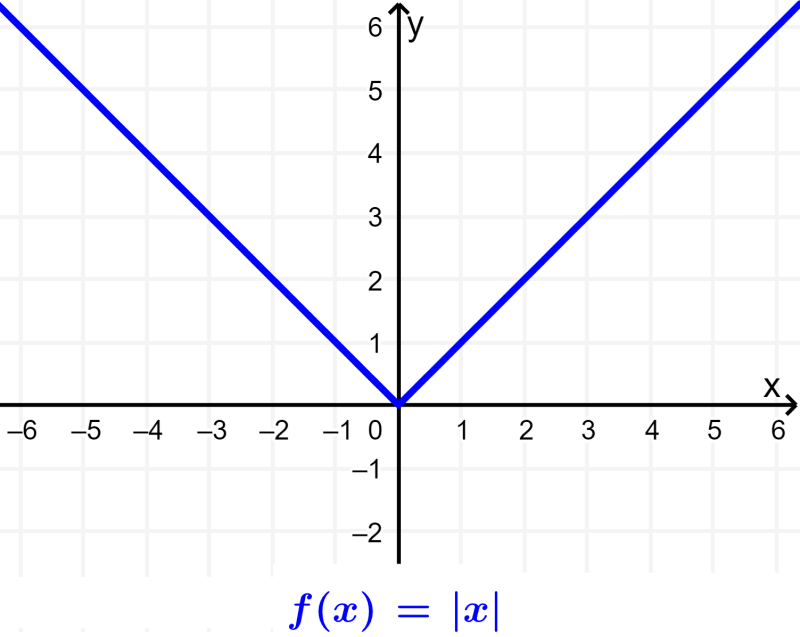
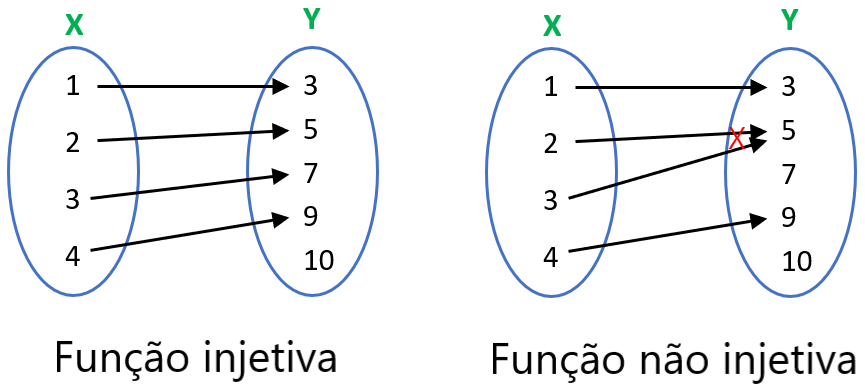
Função injetiva
A função injetiva é uma função em que cada elemento do conjunto final (Y) possui um único elemento do conjunto inicial (X). Essas funções também são conhecidas como um-para-um.
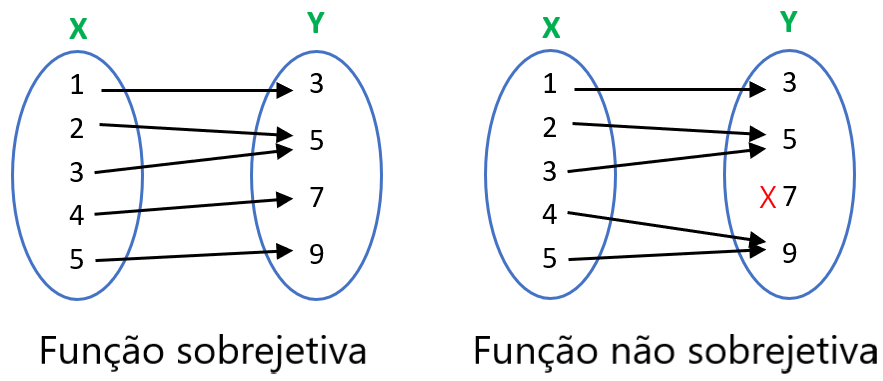
Função sobrejetiva
Uma função sobrejetiva é uma função em que todos os elementos do conjunto final (Y) têm pelo menos um elemento do conjunto inicial (X) que lhes corresponde.
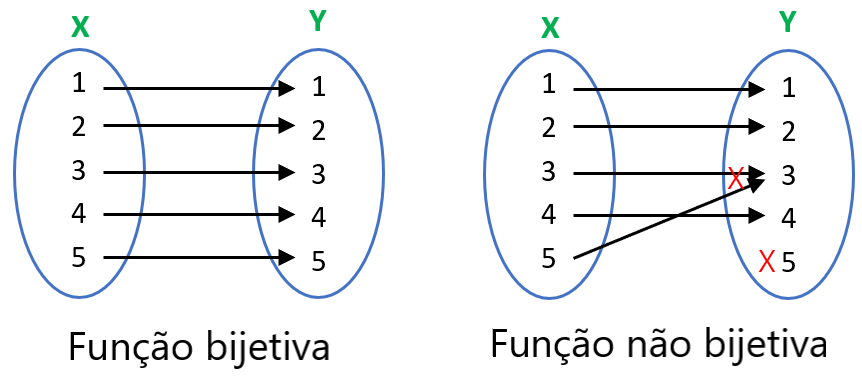
Função bijetiva
Uma função bijetiva é uma função que é injetiva e sobrejetiva ao mesmo tempo.
Veja também
Você quer aprender mais sobre funções? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
