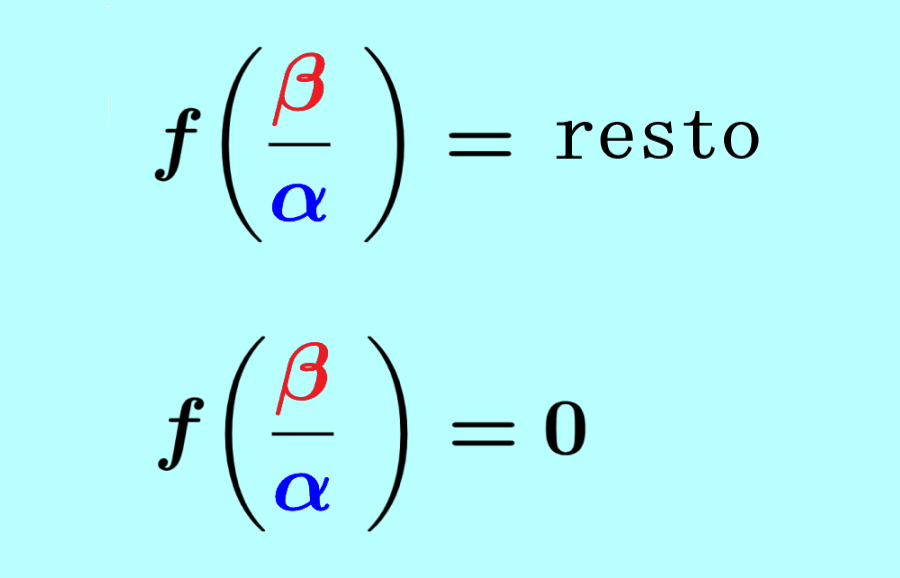Os teoremas do resto e fator são dois teoremas algébricos relacionados à divisão e fatoração de polinômios. O teorema do resto nos permite encontrar o resto quando dividimos um polinômio por uma expressão linear. Por outro lado, o teorema dos fatores nos permite verificar os fatores de um polinômio.
A seguir, aprenderemos tudo relacionado aos teoremas do resto e dos fatores. Veremos suas definições, as provas dos teoremas e alguns exemplos.
O que é o teorema do resto?
O teorema do resto é um teorema algébrico afirmando que quando dividimos um polinômio $latex f(x)$ por $latex (\alpha x-\beta)$, o resto é $latex f\left(\frac{\beta }{ \alpha}\right)$.
Isso significa que podemos usar o teorema do resto para encontrar o resto da divisão de um polinômio pela expressão $latex (\alpha x-\beta)$.
Prova do teorema do resto
O resultado de uma divisão é o quociente. Então, se multiplicarmos o quociente pelo divisor e somarmos o resto, obtemos o polinômio original. Ou seja, temos:
$$f(x)=(\alpha x-\beta)(\text{Quociente})+(\text{Resto})$$
Agora, vamos usar o valor $latex x=\frac{\beta}{\alpha}$, para obter o seguinte:
$$f\left(\frac{\beta}{\alpha}\right)=\left[ \alpha \left(\frac{\beta}{\alpha}\right)-\beta\right](\text{Quociente})+(\text{Resto})$$
$$=\left[ \beta-\beta\right](\text{Quociente})+(\text{Resto})$$
$$=\left[ 0 \right](\text{Quociente})+(\text{Resto})$$
$$=\text{Resto}$$
Vemos que o teorema do resto é verdadeiro, pois usando $latex x=\frac{\beta}{\alpha}$ na função, obtemos o resto da divisão.
O que é o teorema do fator?
O teorema do fator é um teorema algébrico que nos diz que se $latex (\alpha x-\beta)$ é um fator do polinômio $latex f(x)$, então $latex f\left(\frac{ \beta} {\alpha}\right)=0$.
Isso significa que o teorema do fator conecta os fatores e os zeros de um polinômio. O teorema do resto pode ser considerado como uma versão específica deste teorema.
Além disso, podemos usar o teorema do fator para remover zeros conhecidos de um polinômio e deixar todos os zeros desconhecidos intactos, resultando em um polinômio de menor grau com zeros mais fáceis de encontrar.
Prova do teorema do fator
Se $latex (\alpha x-\beta)$ é um fator de $latex f(x)$, então o resto é igual a 0 quando dividimos $latex f(x)$ por $latex (\alpha x -\beta) $.
Então, se usarmos o teorema do resto, podemos mostrar que
$$f\left(\frac{\beta}{\alpha}\right)=0$$
Como usar o teorema do fator
A seguir estão os passos que podemos seguir para usar o teorema dos fatores para identificar os fatores de um polinômio:
Passo 1: Se $latex f(-c)=0$, então $latex (x+ c)$ é um fator do polinômio $latex f(x)$.
Passo 2: Se $latex p(\frac{d}{c})= 0$, então $latex (cx-d)$ é um fator do polinômio $latex f(x)$.
Passo 3: Se $latex p(-\frac{d}{c})= 0$, então $latex (cx+d)$ é um fator do polinômio $latex f(x)$.
Passo 4: Se $latex p(c)=0$ e $latex p(d)=0$, então $latex (x – c)$ e $latex (x -d)$ são fatores do polinômio $latex p(x)$.
O teorema do fator pode ser um método mais fácil de encontrar os fatores de um polinômio em comparação com o método da divisão longa.
Podemos usar este teorema para eliminar zeros conhecidos, deixando todos os zeros desconhecidos intactos para encontrar o polinômio de menor grau.
Se o resto for zero, o teorema do fator é mostrado da seguinte forma:
Se $latex f(c)=0$, o polinômio $latex f(x)$ tem um fator $latex (x-c)$, onde $latex f(x)$ é um polinômio de grau $latex n$.
Exemplos dos teoremas do resto e do fator
Os exemplos a seguir são resolvidos aplicando os teoremas do resto e do fator. Cada exemplo tem uma solução detalhada.
EXEMPLO 1
Encontre o resto quando dividimos o polinômio $latex x^3+5x^2-17x-21$ por $latex x-4$.
Solução: Para resolver isso, temos que usar o teorema do resto.
O teorema do resto nos diz que quando $latex f(x)$ é dividido por $latex x-4$, é $latex f(4)$. Então temos:
$$f(4)=(4)^3+5(4)^2-17(4)-21$$
$latex =64+80-68-21$
$latex =55$
O resto da divisão é 55.
EXEMPLO 2
Quando dividimos o polinômio $latex 3x^3+bx^2-7x+5$ por $latex x+3$, o resto é 17. Encontre o valor de b.
Solução: Neste caso, vamos usar o teorema do resto para formar uma equação e então resolver para b.
Usando o teorema do resto, sabemos que $latex f(-3)=17$. Então temos:
$$3(-3)^3+b(-3)^2-7(-3)+5=17$$
$latex -81+9b+21+5=17$
$latex 9b=72$
$latex b=8$
O valor de b é 8.
EXEMPLO 3
Determine se $latex (x+1)$ é um fator do polinômio $latex f(x) = {x}^2 + x – 2$.
Solução: Para determinar se $latex (x+1)$ é um fator, vamos usar o teorema do fator.
O teorema do fator nos diz que se x+1 é um fator do polinômio, devemos ter $latex f(-1)=0$. Então, usando $latex x=-1$ no polinômio, temos:
$latex f(x) = {x}^2 – x -2$
$latex f(-1) = {(-1)}^2 – (-1) -2$
$latex f(-1) = 1 +1 – 2 $
$latex f(-1) = 0$
Vemos que f(-1) = 0. Isso significa que $latex (x + 2)$ é um fator do polinômio dado.
EXEMPLO 4
$latex (2x-1)$ é um fator do polinômio $latex f(x) = 2{x}^2 – x – 1$?
Solução: Novamente, vamos usar o teorema do fator para resolver isso.
Se 2x-1 é um fator do polinômio, devemos ter $latex f(\frac{1}{2})=0$. Substituindo o valor $latex \frac{1}{2}$ no polinômio, temos:
$latex f(\frac{1}{2}) = 2{x}^2 – x – 1$
$latex f(\frac{1}{2}) = 2{(\frac{1}{2})}^2 – (\frac{1}{2}) – 1$
$latex f(\frac{1}{2}) = 2(\frac{1}{4}) – (\frac{1}{2}) – 1$
$latex f(\frac{1}{2}) = \frac{1}{2} – (\frac{1}{2}) – 1$
Temos $latex f(\frac{1}{2}) = -1$. Isso significa que (2x–1) não é um fator de $latex f(x) = 2{x}^2 – x – 1$.
Veja também
Interessado em aprender mais sobre os teoremas do resto e fator? Você pode olhar para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
