A soma de uma progressão geométrica infinita pode ser calculada quando a razão comum é um número menor que 1 e maior que -1. Para isso, precisamos apenas do valor do primeiro termo e do valor da razão. Em seguida, usamos esses valores em uma fórmula padrão.
A seguir, conheceremos a fórmula que podemos usar para encontrar a soma de uma progressão geométrica infinita. Em seguida, aplicaremos esta fórmula para resolver alguns exercícios.
ÁLGEBRA
Relevante para…
Aprender a encontrar a soma de uma progressão geométrica infinita.
ÁLGEBRA
Relevante para…
Aprender a encontrar a soma de uma progressão geométrica infinita.
Fórmula para a soma de uma progressão geométrica infinita
A soma de uma progressão geométrica infinita pode ser calculada quando temos $latex -1<r<1$. Por exemplo, considere a seguinte progressão:
$$1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…\left(\frac{1}{2}\right)^n$$
Vemos que à medida que o número de termos aumenta, o valor de cada termo fica cada vez menor.
Ou seja, como $latex n \rightarrow \infty$, o termo $latex \left(\frac{1}{2}\right)^n\rightarrow 0$, portanto a soma da progressão infinita tem um valor específico.
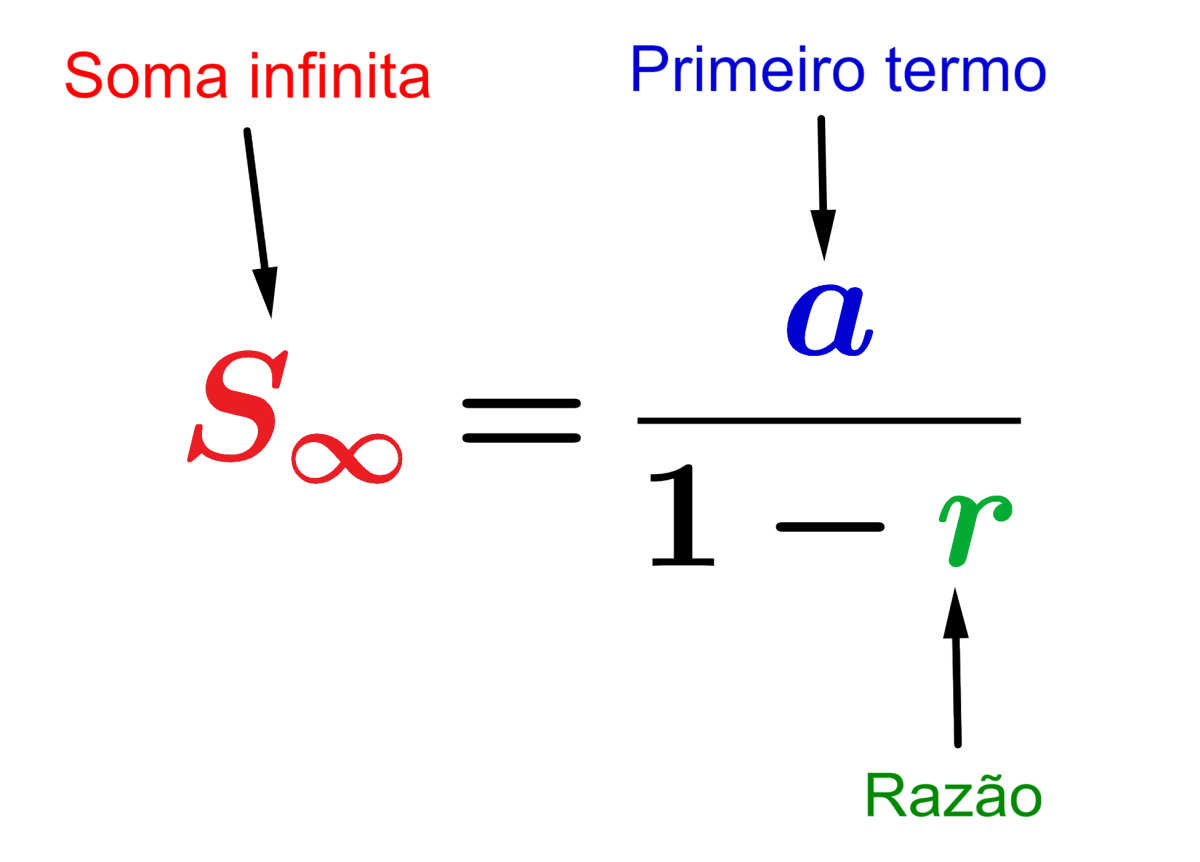
Para encontrar a soma de uma progressão geométrica infinita, usamos a seguinte fórmula:
$$S_{\infty}= \frac{a}{1-r}$$
onde $latex -1<r<1$. Se a razão comum não atender a essa condição, a soma infinita não existe.
Prova da fórmula da soma de progressões geométricas infinitas
Lembre-se de que podemos encontrar a soma dos primeiros $latex n$ termos de qualquer progressão geométrica usando a seguinte fórmula:
$$S_{n}=\frac{a(1-r^n)}{1-r}$$
Se a razão comum satisfaz a condição $latex -1<r<1$, como $latex n\rightarrow \infty$, temos $latex r^n\rightarrow 0$.
Basicamente, isso significa que o termo $latex r^n$ da progressão fica cada vez menor até que seu valor se aproxime cada vez mais de 0.
Então, como $latex n\rightarrow \infty$, temos:
$$S_{n}\rightarrow \frac{a(1-0)}{1-r}=\frac{a}{1-r}$$
Portanto, provamos que a soma infinita de uma progressão geométrica onde $latex -1<r<1$ é dada por:
$$S_{\infty}=\frac{a}{1-r}$$
Notamos que a prova começa assumindo que $latex -1<r<1$. Se não for esse o caso, a soma infinita não existe.
Exemplos resolvidos da soma de progressões geométricas infinitas
EXEMPLO 1
Encontre a soma infinita da seguinte progressão geométrica:
$$1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…$$
Solução
Começamos escrevendo as informações que sabemos:
- Primeiro termo: $latex a=1$
- Razão: $latex r=\frac{1}{2}$
Agora, usamos a fórmula para a soma infinita de uma progressão geométrica:
$$S_{\infty}=\frac{a}{1-r}$$
$$=\frac{1}{1-\frac{1}{2}}$$
$$=\frac{1}{\frac{1}{2}}$$
$latex S_{\infty}=2$
EXEMPLO 2
Encontre a soma infinita de uma progressão geométrica na qual o primeiro termo é igual a -3 e a razão é igual a $latex -\frac{1}{2}$.
Solução
Neste caso, temos os seguintes valores
- Primeiro termo: $latex a=-3$
- Razão: $latex r=-\frac{1}{2}$
Aplicando a fórmula da soma infinita de uma progressão geométrica, temos:
$$S_{\infty}=\frac{a}{1-r}$$
$$=\frac{-3}{1+\frac{1}{2}}$$
$$=\frac{-3}{\frac{3}{2}}$$
$latex S_{\infty}=-2$
EXEMPLO 3
Encontre a soma infinita da seguinte progressão geométrica:
$$2+\frac{1}{2}+\frac{1}{8}+\frac{1}{32}+…$$
Solução
Neste caso, temos o seguinte
- Primeiro termo: $latex a=2$
- Razão: $latex r=\frac{1}{4}$
Quando usamos a fórmula da soma infinita, temos:
$$S_{\infty}=\frac{a}{1-r}$$
$$=\frac{2}{1-\frac{1}{4}}$$
$$=\frac{2}{\frac{3}{4}}$$
$$S_{\infty}=\frac{8}{3}$$
EXEMPLO 4
Encontre o resultado da seguinte soma:
$$\sum_{r=1}^{\infty}\left(\frac{1}{5}\right)^r$$
Solução
Aqui, temos a soma da progressão geométrica escrita na forma de somatório. Encontramos o valor do primeiro termo usando $latex r=1$.
A razão comum é o número dentro dos parênteses, então temos:
- Primeiro termo: $latex a=\frac{1}{5}$
- Razão: $latex r=\frac{1}{5}$
Usando a fórmula da soma infinita com esses valores, temos:
$$S_{\infty}=\frac{a}{1-r}$$
$$=\frac{\frac{1}{5}}{1-\frac{1}{5}}$$
$$=\frac{\frac{1}{5}}{\frac{4}{5}}$$
$$=\frac{5}{20}$$
$$S_{\infty}=\frac{1}{4}$$
EXEMPLO 5
Escreva o decimal recursivo 0,3232… como a soma de uma progressão geométrica e, em seguida, escreva o decimal como um número racional.
Solução
Para resolver este exercício, começamos escrevendo o decimal como a soma de uma progressão geométrica:
$$0,323232…= \frac{32}{100}+\frac{32}{10000}+\frac{32}{1000000}+…$$
Agora, identificamos os seguintes valores:
- $latex a=\frac{32}{100}$
- $latex r=\frac{1}{100}$
Como $latex -1<r<1$, podemos calcular o valor da soma infinita:
$$S_{\infty}=\frac{a}{1-r}$$
$$=\frac{\frac{32}{100}}{1-\frac{1}{100}}$$
$$=\frac{\frac{32}{100}}{\frac{99}{100}}$$
$$S_{\infty}=\frac{32}{99}$$
Assim, o decimal recorrente 0,3232…, pode ser escrito como $latex \frac{32}{99}$.
EXEMPLO 6
Expresse o decimal recorrente 0,7272… como uma fração em sua forma mais simples.
Solução
Escrevemos para o decimal como uma progressão geométrica:
$$0,727272…= \frac{72}{100}+\frac{72}{10000}+\frac{72}{1000000}+…$$
Agora, podemos ver que a progressão tem os seguintes valores:
- $latex a=\frac{72}{100}$
- $latex r=\frac{1}{100}$
Como $latex -1<r<1$, podemos calcular o valor da soma infinita:
$$S_{\infty}=\frac{a}{1-r}$$
$$=\frac{\frac{72}{100}}{1-\frac{1}{100}}$$
$$=\frac{\frac{72}{100}}{\frac{99}{100}}$$
$$=\frac{72}{99}$$
$$S_{\infty}=\frac{8}{11}$$
Assim, o decimal recorrente 0,7272…, pode ser escrito como $latex \frac{8}{11}$.
Soma de progressões geométricas infinitas – Exercícios para resolver
Encontre a soma infinita da seguinte progressão geométrica $$4+\frac{4}{3}+\frac{4}{9}+…$$
Escreva a resposta na caixa.
Veja também
Interessado em aprender mais sobre progressões geométricas? Você pode olhar para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
