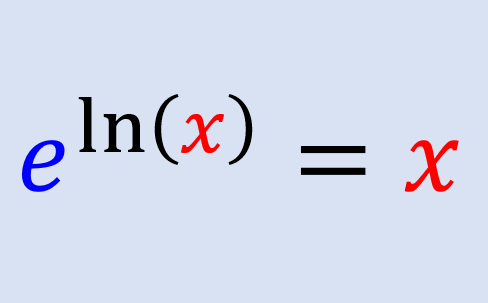Com as regras dos logaritmos naturais, podemos simplificar as expressões logarítmicas e reescrevê-las de maneiras mais convenientes. Temos onze regras principais de logaritmos naturais. Com essas onze regras, podemos expandir os logaritmos naturais, condensá-los e resolver equações logarítmicas. Embora essas regras sejam especificadas para logaritmos naturais, as regras dos logaritmos se aplicam a logaritmos de qualquer base.
A seguir, conheceremos as onze principais regras dos logaritmos. Além disso, vamos resolver alguns exercícios de logaritmo para aplicar essas regras.
Quais são as regras dos logaritmos naturais?
Lembre-se de que um logaritmo natural é um logaritmo com base e. O número e é chamado de constante natural e tem um valor aproximado de 2,71828. O logaritmo natural é denotado como ln. O número e tem diversas aplicações em diversas áreas como matemática, economia, entre outras.
Como e aparece em muitas áreas, muitas pessoas precisam calcular o logaritmo com base e frequentemente, então houve a necessidade de criar um atalho com o logaritmo natural e defini-lo como um logaritmo com base e.
A seguir estão as leis mais importantes dos logaritmos naturais:
1. Regra do produto
Se tivermos um logaritmo natural de um produto, podemos escrevê-lo como a soma dos logaritmos de cada fator separadamente:
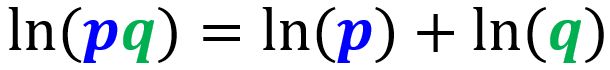
2. Regra do quociente
Se tivermos um logaritmo natural de um quociente, podemos reescrevê-lo como o logaritmo natural do numerador menos o logaritmo natural do denominador:
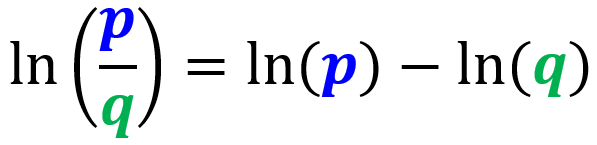
3. Regra de potência
O logaritmo natural de um argumento exponencial pode ser reescrito como o expoente multiplicado pelo logaritmo da base (sem o expoente):
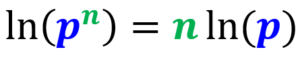
4. Regra do logaritmo de recíproco
O logaritmo natural do recíproco de x é o oposto do logaritmo natural de x:
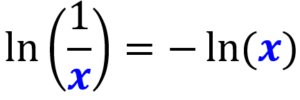
5. Regra do logaritmo natural de 1
O logaritmo natural de 1 é igual a zero:
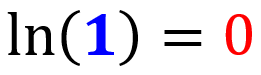
6. Regra do logaritmo natural de e
O logaritmo natural do número natural, e, é igual a 1:
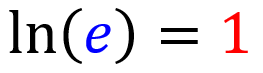
7: Regra do logaritmo natural de zero
O logaritmo natural de zero é indefinido:
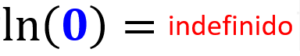
8: Regra do logaritmo natural de um número negativo
O logaritmo natural de um número negativo também é indefinido.
9: Regra do logaritmo natural do infinito
O logaritmo natural do infinito é igual ao infinito:
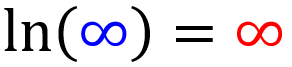
10: Regra do logaritmo natural de exponencial e
O logaritmo natural do exponencial e é igual ao expoente de e:
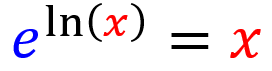
11: Regra de e elevada ao logaritmo natural
O número e elevado ao logaritmo natural de um número é igual ao número:
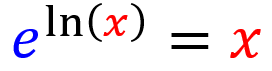
Exercícios sobre regras de logaritmos naturais resolvidos
Os exercícios a seguir usam as regras dos logaritmos naturais descritas acima. Recomenda-se que você tente resolver os exercícios sozinho antes de examinar a resposta.
EXERCÍCIO 1
Simplifique a seguinte expressão: $latex \ln(8)+\ln(10)$.
Solução
Temos uma soma de logaritmos, então podemos aplicar a lei do produto para simplificar:
$latex \ln(8)+\ln(10)=\ln(8\times 10)$
$latex =\ln(80)$
Podemos deixar o logaritmo dessa forma ou resolvê-lo, temos:
$latex \ln(80)\approx 4.382$
EXERCÍCIO 2
Simplifique a expressão logarítmica: $latex \ln(72)-\ln(3)$.
Solução
Neste caso, temos uma subtração dos logaritmos naturais, para que possamos aplicar a lei do quociente:
$latex \ln(72)-\ln(3)=\ln(\frac{72}{3})$
$latex =\ln(24)$
Podemos deixar o logaritmo natural assim ou podemos aplicá-lo:
$latex \ln(24)\approx 3.178$
EXERCÍCIO 3
Qual é o valor de $latex \ln({{e}^{15}})$?
Solução
Aqui, podemos usar a regra do logaritmo natural de e exponencial. Esta regra nos diz que quando temos o logaritmo natural de e elevado a um expoente, isso é equivalente ao expoente:
$latex \ln({{e}^{15}})=15$
EXERCÍCIO 4
Simplifique a seguinte expressão $latex \ln(100)-\ln(5)+\ln(4)$.
Solução
Nesta expressão, temos subtrações e adições de logaritmos naturais. Podemos formar um único logaritmo aplicando a lei do quociente e a regra do produto. Então, temos:
$latex \ln(100)-\ln(5)+\ln(4)=\ln(\frac{100 \times 4}{5})$
$latex =\ln(\frac{400}{5})$
$latex =\ln(80)$
Agora, podemos deixar o logaritmo assim ou podemos calculá-lo para obter:
$latex \ln(80)\approx 4.382$
EXERCÍCIO 5
Simplifique a expressão: $latex 2\ln(5)+\ln(40)-3\ln(10)$.
Solução
Começamos usando a regra de potência para reescrever os logaritmos naturais.
$latex 2\ln(5)+\ln(40)-3\ln(10)$
$latex =\ln({{5}^2})+\ln(40)-\ln({{10}^3})$
$latex =\ln(25)+\ln(40)-\ln(1000)$
Agora, podemos usar a regra do produto e a regra do quociente para obter um único logaritmo:
$latex =\ln(\frac{25\times 40}{1000})$
$latex =\ln(1)$
Finalmente, aplicamos a regra do logaritmo natural de 1 para resolver:
$latex \ln(1)=0$
EXERCÍCIO 6
Escreva a versão expandida do logaritmo natural: $latex\ln({{e}^3}{{x}^3}{{y}^4})$.
Solução
Podemos aplicar a regra do produto para separar os fatores e formar uma soma dos logaritmos naturais:
$latex \ln({{e}^3}{{x}^3}{{y}^4})=\ln({{e}^3})+\ln({{x}^3})+\ln({{y}^4})$
Agora, podemos usar a regra de potência para reescrever os expoentes como uma multiplicação de cada logaritmo individual:
$latex =3\ln(e)+3\ln(x)+4\ln(y)$
$latex =3(1)+3\ln(x)+4\ln(y)$
$latex =3+3\ln(x)+4\ln(y)$
Exercícios sobre regras de logaritmos naturais para resolver
Teste seu conhecimento das regras dos logaritmos naturais resolvendo os exercícios a seguir. Se precisar de ajuda, você pode consultar a lista de regras dos logaritmos naturais ou os exercícios resolvidos acima.
Veja também
Você quer aprender mais sobre logaritmos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
