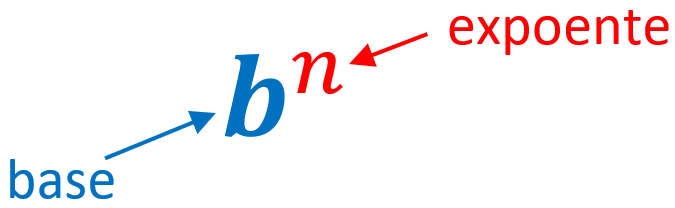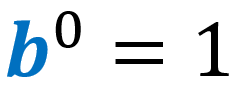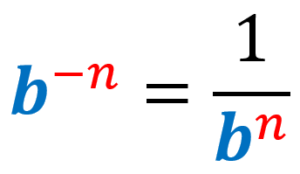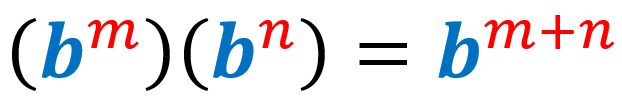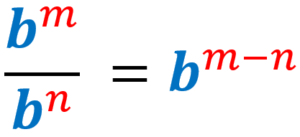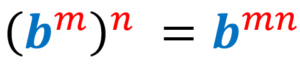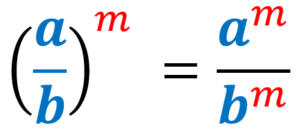Regras das potências são regras algébricas que nos permitem simplificar expressões com expoentes. Essas regras são usadas para obter expressões mais simples ou até mesmo resolver expressões. Dominar as regras de expoentes básicos tornará seu estudo de álgebra mais fácil e produtivo.
Partes de expressões exponenciais
Vamos começar explorando as partes de uma expressão exponencial.
Uma expressão exponencial é composta de duas partes. A primeira parte é a base, que “mantém” o expoente, que é a segunda parte e está localizado na parte superior direita, como pode ser visto na ilustração:
- O expoente é o número que indica quantas vezes a base será multiplicada por ela mesma.
- A base é o número ou variável que está sendo multiplicado repetidamente.
Por exemplo, vamos tentar escrever $latex 3 \times 3 \times 3 \times 3$ na notação de expoente.
O número 3 é o número que está sendo multiplicado repetidamente, então sabemos imediatamente que 3 é a base. Notamos que foi escrito 4 vezes. Este número indica quantas vezes a base está sendo multiplicada, portanto sabemos que é o expoente.
A base de uma expressão algébrica também pode ser uma letra ou variável. Por exemplo, se tivermos a variável x repetidamente multiplicada por si mesma, podemos escrevê-la em notação de expoente:
Resumo rápido das regras das potências
Nas regras a seguir, a e b são números reais diferentes de zero e m e n são inteiros:
1) Regra potência zero
2) Regra de expoentes negativos:
3) Regra do produto dos expoentes:
4) Regra do quociente de expoentes:
5) Potência de uma potência de expoentes:
6) Potência de um produto de expoentes:
7) Potência de um quociente de expoentes:
Descrição das regras das potências com exemplos
1) Regra potência zero
Qualquer número elevado à potência de zero é igual a 1.
EXEMPLOS
- Simplifique a expressão exponencial $latex {{4}^0}$.
Aqui, a base é 4 e o expoente é 0. Podemos aplicar a regra do zero diretamente. Então $latex {{4}^0}=1$.
- Simplifique a expressão exponencial $latex {{(3x {{y}^2})}^0}$.
A base é a expressão inteira que está entre parênteses. Isto é mais facil do que parece. Contanto que as variáveis x e y sejam diferentes de zero, a regra zero se aplica e temos $latex {{(3x{{y}^2})}^0}=1$.
2) Regra de expoentes negativos
Qualquer número elevado a um expoente negativo não está em sua forma padrão. Teremos que reorganizá-lo. Para conseguir isso, movemos a base com o expoente negativo para o lado oposto da fração e, em seguida, tornamos o expoente positivo.
EXEMPLOS
- Simplifique a expressão exponencial $latex {{2}^{{-3}}}$.
Aqui, a base é 2 e tem um expoente negativo de -3. Usando a regra dos expoentes negativos, podemos movê-lo para o denominador da fração e alterar o expoente de negativo para positivo:
$latex {{2}^{{-3}}}=\frac{1}{{{{2}^{3}}}}$
$latex =\frac{1}{8}$
- Simplifique a expressão exponencial $latex \frac{1}{{{{x}^{-5}}}}$.
A base com expoente negativo está no denominador. Podemos movê-lo para o numerador e alterar o expoente de negativo para positivo:
$latex \frac{1}{{{{x}^{-5}}}}={{x}^{{5}}}$
3) Regra do produto dos expoentes
Quando multiplicamos duas expressões exponenciais, onde temos a mesma base, copiamos a base e adicionamos seus expoentes. Aqui, assumimos que a base b é diferente de zero e os expoentes m e n são inteiros.
EXEMPLOS
- Simplifique o produto de expressões exponenciais $latex ({{x}^{{3}}})({{x}^{{5}}})$.
Usando a regra do produto dos expoentes, simplesmente copiamos a base e adicionamos os expoentes:
$latex ({{x}^{{3}}})({{x}^{{5}}})={{x}^{{5+3}}}$
$latex ={{x}^{{8}}}$
- Simplifique o produto de expressões exponenciais $latex (2{{x}^{{2}}}{{y}^{{3}}})(3{{x}^{{3}}}{{y}^{{4}}})$.
Nesse caso, cada parêntese contém um número, a variável x e a variável y. Para resolver isso, temos que garantir que multiplicamos apenas os termos do mesmo tipo, ou seja, multiplicamos os números e as variáveis separadamente:
$latex (2{{x}^{{2}}}{{y}^{{3}}})(3{{x}^{{3}}}{{y}^{{4}}})$
$latex =(2\times 3)({{x}^{{2}}}\times {{x}^{{3}}})({{y}^{{3}}}\times {{y}^{{4}}})$
$latex =6({{x}^{{2+3}}})({{y}^{{3+4}}})$
$latex =6({{x}^{{5}}})({{y}^{{7}}})$
4) Regra do quociente de expoentes
Quando temos uma divisão de expressões exponenciais com a mesma base, copiamos a base e subtraímos o expoente da expressão do numerador pelo expoente da expressão do denominador.
Aqui, assumimos que a base b é diferente de zero e os expoentes m e n são inteiros.
EXEMPLOS
- Simplifique a divisão de expressões exponenciais $latex \frac{{{{x}^{4}}}}{{{{x}^{2}}}}$.
Aplicando a regra do quociente, copiamos a base e subtraímos o expoente abaixo do expoente acima:
$latex \frac{{{{x}^{4}}}}{{{{x}^{2}}}}={{{x}^{4-2}}}$
$latex ={{{x}^{2}}}$
- Simplifique a divisão de expressões exponenciais $latex \frac{{{{x}^{3}}}{{{y}^{4}}}}{{{{x}^{4}}}{{{y}^{3}}}}$.
Vemos que temos as variáveis x e y, portanto, aplicamos a regra de quociente a cada variável separadamente:
$latex \frac{x^3y^4}{x^4y^3}=(x^{3-4})(y^{4-3})$
$latex ={{{x}^{-1}}}{{{y}^{1}}}$
$latex =\frac{y}{x}$
5) Potência de uma potência de expoentes
Quando uma expressão exponencial é elevada a uma potência, copiamos a base e multiplicamos os expoentes. Novamente, assumimos que a base é diferente de zero e os expoentes são números inteiros.
EXEMPLOS
- Simplifique a expressão exponencial $latex {{\left( {{{x}^{2}}} \right)}^{3}}$.
Esta expressão possui um expoente interno e um expoente externo. A regra de potência de uma potência nos diz para copiar a base e multiplicar os expoentes:
$latex {{\left( {{{x}^{2}}} \right)}^{3}}= {{{x}^{(2)(3)}}}$
$latex ={{{x}^{6}}}$
- Simplifique a expressão exponencial $latex {{\left( {{{x}^{3}}}{{{y}^{5}}} \right)}^{4}}$.
Aplicamos a regra de potência de uma potência separadamente:
$latex {{\left( {{{x}^{3}}}{{{y}^{5}}} \right)}^{4}}={{{x}^{(3)(4)}}}{{{y}^{(4)(5)}}}$
$latex ={{{x}^{12}}}{{{y}^{20}}}$
6) Potência de um produto de expoentes
Quando temos o produto de dois ou mais fatores elevados a uma potência, copiamos cada fator e, em seguida, multiplicamos o expoente externo por seu expoente. Temos que fazer isso para cada fator entre parênteses. Aqui, assumimos que as bases são diferentes de zero e os expoentes são números inteiros.
EXEMPLOS
- Simplifique a expressão exponencial $latex {{\left( {{{3}^{2}}{{x}^{3}}{{y}^{4}}} \right)}^{3}}$.
Aqui temos três fatores, cada um com expoentes. Simplesmente temos que copiar cada fator e multiplicar seu expoente pelo expoente externo:
$latex {{\left( {{{3}^{2}}{{x}^{3}}{{y}^{4}}} \right)}^{3}}=({{{3}^{(2)(3)}}{{x}^{(3)(3)}}{{y}^{(4)(3)}}})$
$latex ={{{3}^{6}}{{x}^{9}}{{y}^{12}}}$
7) Potência de um quociente de expoentes
Quando um quociente é elevado a uma potência, copiamos o fator para o numerador e multiplicamos seu expoente pelo expoente externo. Então fazemos o mesmo com o fator no denominador. Assumimos que as bases são diferentes de zero e que os expoentes são números inteiros.
EXEMPLOS
- Simplifique a expressão exponencial $latex {{\left( {\frac{{{{x}^{3}}}}{{{{y}^{5}}}}} \right)}^{4}}$.
Usando a regra de potência de um quociente de expoentes. Copiamos as bases do numerador e do denominador e multiplicamos seus expoentes pelo expoente externo:
$latex {{\left( {\frac{{{{x}^{3}}}}{{{{y}^{5}}}}} \right)}^{4}}={\frac{{{{x}^{(3)(4)}}}}{{{{y}^{(5)(4)}}}}}$
$latex ={\frac{{{{x}^{12}}}}{{{{y}^{20}}}}}$
Veja também
Você quer aprender mais sobre expressões com expoentes? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
