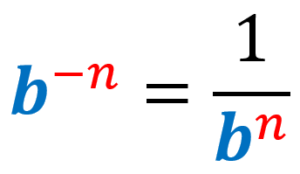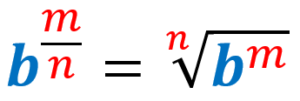Expoente Negativo em Fração – Regra e Exercícios

EXEMPLO 1

Simplifique a expressão $latex {{3}^{-2}}$.

Solução: Sabemos que o expoente negativo significa que a base pertence ao outro lado da fração. Mas vemos que não há linha de fração. No entanto, sabemos que isso pode ser escrito como uma fração com denominador 1.

Então, começamos convertendo a expressão em uma fração da maneira que todas as expressões podem ser convertidas em frações: colocando-a no 1. Portanto, temos o seguinte:

$latex {{3}^{{-2}}}=\frac{{{{3}^{{-2}}}}}{1}=\frac{1}{{{{3}^{2}}}}=\frac{1}{9}$

EXEMPLO 2

Escreva $latex {{x}^{-3}}$ usando apenas expoentes positivos.

Solução: Novamente, sabemos que devemos mudar a base para o outro lado da fração e mudar o expoente de negativo para positivo. Formamos uma fração colocando a expressão sobre 1.

Então, começamos convertendo a expressão em uma fração onde o denominador é 1 e depois simplificamos. Portanto, temos o seguinte:

$latex {{x}^{{-3}}}=\frac{{{{x}^{{-3}}}}}{1}=\frac{1}{{{{x}^{3}}}}$

EXEMPLO 1

• Simplifique a fração $latex \frac{{{{4}^{{-2}}}}}{{{{8}^{{-2}}}}}$.

Solução: Podemos aplicar a regra do expoente negativo separadamente ao numerador e ao denominador e então simplificar a expressão resultante. Então nós temos:

$latex \frac{{{{4}^{{-2}}}}}{{{{8}^{{-2}}}}}=\frac{1}{{{{4}^{2}}}}\times \frac{{{{8}^{2}}}}{1}$

$latex =\frac{{{{8}^{{2}}}}}{{{{4}^{{2}}}}}$

$latex =\frac{64}{16}$

$latex =4$

Então, descobrimos que $latex \frac{{{{4}^{{-2}}}}}{{{{8}^{{-2}}}}}$é equivalente a 4.

EXEMPLO 2

• Simplifique a fração $latex \frac{{3{{x}^{{-2}}}y}}{{xy}}$.

Solução: Neste caso, apenas a expressão $latex {{{x}^{{-2}}}}$ possui um expoente negativo. Então, mudamos essa expressão do numerador para o denominador e a tornamos positiva:

$latex \frac{{3{{x}^{{-2}}}y}}{{xy}}=\frac{{3y}}{{{{x}^{2}}\left( {xy} \right)}}$

$latex =\frac{{3y}}{{{{x}^{3}}y}}$

Agora cancelamos os termos semelhantes no numerador e no denominador:

$latex \frac{{3y}}{{{{x}^{3}}y}}=\frac{{3}}{{{{x}^{3}}}}$

EXEMPLO 1

• Simplifique a fração $latex \frac{{{{4}^{{-\frac{1}{2}}}}}}{{{{6}^{{-2}}}}}$.

Solução: No numerador, temos um expoente fracionário negativo e no denominador, um expoente negativo. Então, começamos aplicando a regra dos expoentes negativos:

$latex \frac{{{{4}^{{-\frac{1}{2}}}}}}{{{{6}^{{-2}}}}}=\frac{{{{6}^{2}}}}{{{{4}^{{\frac{1}{2}}}}}}$

Agora, temos expoentes positivos no numerador e no denominador, mas temos um expoente fracionário no denominador, então aplicamos a regra dos expoentes fracionários lá:

$latex =\frac{{{{6}^{2}}}}{{\sqrt{4}}}$

Agora, resolvemos os expoentes e simplificamos:

$latex =\frac{{36}}{2}$

$latex =18$

EXEMPLO 2

• Simplifique a expressão $$\frac{{{{x}^{{-\frac{3}{2}}}}}}{{{{{16}}^{{-\frac{1}{4}}}}{{y}^{{-\frac{1}{2}}}}}}$$

Solução: Todos os expoentes são negativos, então começamos aplicando a regra dos expoentes negativos:

$$\frac{{{{x}^{{-\frac{3}{2}}}}}}{{{{{16}}^{{-\frac{1}{4}}}}{{y}^{{-\frac{1}{2}}}}}}=\frac{{{{{16}}^{{\frac{1}{4}}}}{{y}^{{\frac{1}{2}}}}}}{{{{x}^{{\frac{3}{2}}}}}}$$

Agora, temos expoentes positivos no numerador e no denominador. Podemos aplicar a regra do expoente fracionário:

$latex =\frac{{\sqrt[4]{{16}}\sqrt{y}}}{{\sqrt{{{{x}^{3}}}}}}$

Agora, simplificamos:

$latex =\frac{{2~\sqrt{y}}}{{\sqrt{{{{x}^{3}}}}}}$

EXERCÍCIO 1

• Simplifique a expressão $latex \frac{{{{x}^{2}}}}{{{{x}^{{-3}}}}}$.

Solução: Esta expressão possui apenas o denominador com expoente negativo. Então, mudamos o denominador para o numerador com um expoente positivo:

$latex \frac{{{{x}^{2}}}}{{{{x}^{{-3}}}}}=\frac{{{{x}^{2}}{{x}^{3}}}}{1}$

Agora só temos expoentes positivos e podemos aplicar a regra do produto dos expoentes para simplificar:

$latex ={{x}^{{2+3}}}={{x}^{5}}$

EXERCÍCIO 2

• Simplifique a expressão $$\frac{{{{{25}}^{{-\frac{1}{2}}}}}}{{{{{16}}^{{-\frac{1}{4}}}}}}$$

Solução: Neste caso, temos expoentes negativos fracionários. Então, começamos aplicando a regra dos expoentes negativos para mudar do numerador para o denominador e vice-versa e mudar de negativo para positivo:

$$\frac{{{{{25}}^{{-\frac{1}{2}}}}}}{{{{{16}}^{{-\frac{1}{4}}}}}}=\frac{{{{{16}}^{{\frac{1}{4}}}}}}{{{{{25}}^{{\frac{1}{2}}}}}}$$

Agora, temos expoentes positivos no numerador e no denominador. Portanto, podemos aplicar a regra dos expoentes fracionários para formar radicais:

$latex =\frac{{\sqrt[4]{{16}}}}{{\sqrt{{25}}}}$

Finalmente, calculamos os radicais:

$latex =\frac{2}{5}$

EXERCÍCIO 3

• Escreva a expressão $latex {{\left( {\frac{{{{x}^{{-3}}}}}{{{{y}^{{-2}}}}}} \right)}^{{-2}}}$ apenas com expoentes positivos.

Solução: Começamos observando que temos um expoente negativo fora dos parênteses. Isso significa que o numerador deve ser movido para baixo e o denominador deve ser movido para cima. Ou seja, devemos inverter a fração que está dentro dos parênteses:

$latex {{\left( {\frac{{{{x}^{{-3}}}}}{{{{y}^{{-2}}}}}} \right)}^{{-2}}}={{\left( {\frac{{{{y}^{{-2}}}}}{{{{x}^{{-3}}}}}} \right)}^{2}}$

Agora que temos um expoente positivo, usamos a regra da potência de uma potência para aplicar o expoente separadamente ao numerador e denominador:

$latex =\frac{{{{{\left( {{{y}^{{-2}}}} \right)}}^{2}}}}{{{{{\left( {{{x}^{{-3}}}} \right)}}^{2}}}}$

$latex =\frac{{{{y}^{{-4}}}}}{{{{x}^{{-6}}}}}$

Finalmente, usamos a regra dos expoentes negativos novamente e invertemos a fração:

$latex =\frac{{{{x}^{6}}}}{{{{y}^{4}}}}$