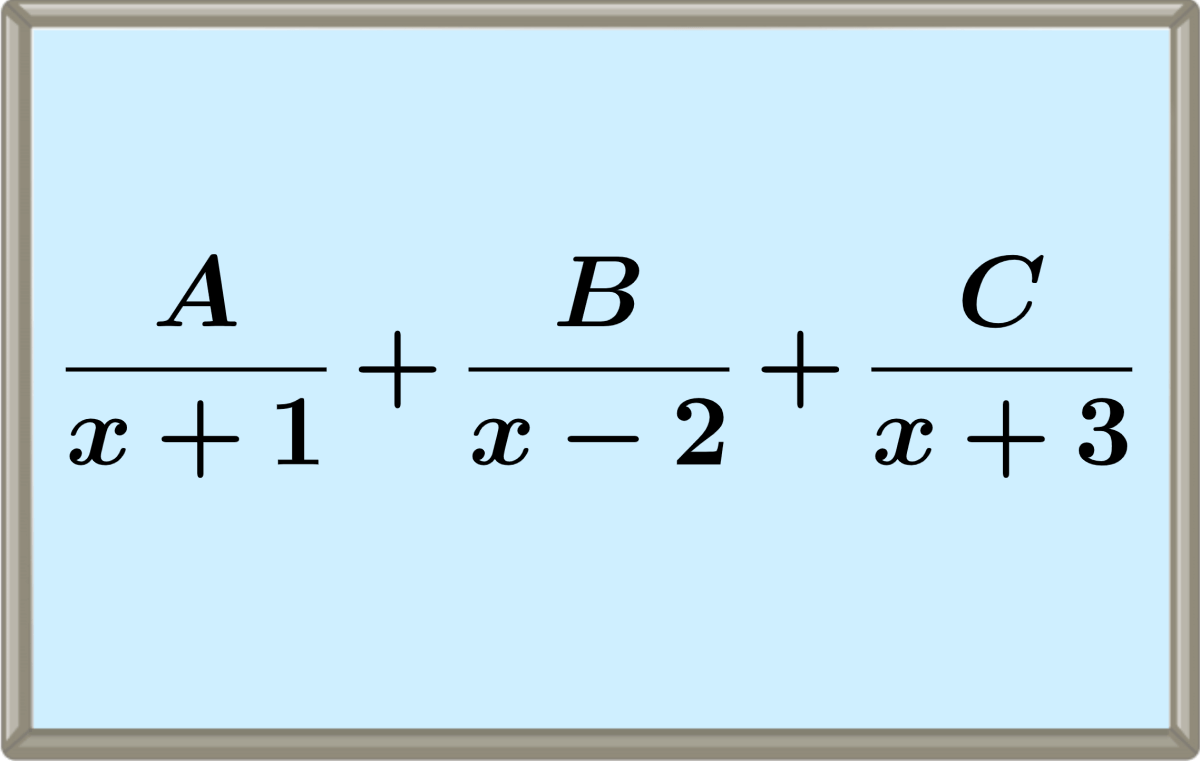A decomposição de uma fração em frações parciais pode ser considerada o processo inverso de adição ou subtração de duas, ou mais frações. Existem quatro casos principais de frações parciais: denominador com fatores lineares, denominador com fator quadrático irredutível, denominador com fator repetido e frações impróprias.
A seguir, vamos conhecer estes quatro casos de fracções parciais em detalhe. Além disso, vamos olhar para alguns exemplos para aplicar os conceitos.
Caso 1: Denominador com fatores lineares
Cada fator linear $latex (ax+b)$ no denominador tem uma fração parcial correspondente da forma
$$\frac{A}{ax+b}$$
onde $latex a,~b$ e $latex A$ são constantes.
Por exemplo, se tivermos a seguinte fração
$$\frac{3x-1}{(x+3)(x-2)}$$
as suas fracções parciais terão a seguinte forma:
$$\frac{3x-1}{(x+3)(x-2)}=\frac{A}{x+3}+\frac{B}{x-2}$$
Os valores das constantes A e B podem ser encontrados multiplicando a expressão inteira pelo denominador da fração original.
Então, podemos usar dois métodos diferentes, como mostrado nos exemplos a seguir.
EXEMPLO 1
Decompor a fracção seguinte em fracções parciais:
$$\frac{3x-1}{(x+3)(x-2)}$$
Solução
Como temos dois fatores lineares $latex (x+3)$ e $latex (x-2)$, sua decomposição em frações parciais é:
$$\frac{3x-1}{(x+3)(x-2)}=\frac{A}{x+3}+\frac{B}{x-2}$$
Agora, multiplicamos a expressão inteira por $latex (x+3)(x-2)$ para obter:
$$3x-1=A(x-2)+B(x+3)$$
Podemos usar dois métodos diferentes para encontrar os valores das constantes. Usando o primeiro método, substituímos $latex x=2$ para eliminar a constante A e encontrar o valor de B:
$$3(2)-1=A(2-2)+B(2+3)$$
$latex 5=5B$
$latex B=1$
Depois, substituímos $latex x=-3$ para encontrar o valor de A:
$$3(-3)-1=A(-3-2)+B(-3+3)$$
$latex -10=-5A$
$latex A=2$
O segundo método consiste em expandir o lado direito da equação para obter:
$$3x-1=A(x-2)+B(x+3)$$
$$3x-1=Ax-2A+Bx+3B$$
Comparando os coeficientes dos termos com a variável x, temos:
$latex 3=A+B$
Comparando os termos constantes, temos:
$latex -1=-2A+3B$
Formando um sistema de equações e resolvendo simultaneamente, temos $latex A=2$ e $latex B=1$, semelhante ao método anterior.
Então,
$$\frac{3x-1}{(x+3)(x-2)}=\frac{2}{x+3}+\frac{1}{x-2}$$
EXEMPLO 2
Expresse a seguinte fração em frações parciais
$$\frac{9x^2+34x+14}{(x+2)(x^2-x-12)}$$
Solução
Neste caso, podemos começar por factorar o denominador para obter apenas factores lineares:
$$x^2-x-12=(x+3)(x-4)$$
Então, temos:
$$\frac{9x^2+34x+14}{(x+2)(x^2-x-12)}=\frac{9x^2+34x+14}{(x+2)(x+3)(x-4)}$$
Agora, como só temos factores lineares no denominador, podemos escrever como se segue:
$$\frac{9x^2+34x+14}{(x+2)(x+3)(x-4)}=\frac{A}{x+2}+\frac{B}{x+3}+\frac{C}{x-4}$$
Se multiplicarmos a expressão inteira por $latex (x+2)(x+3)(x-4)$, temos:
$$ 9x^2+34x+14=A(x+3)(x-4)+B(x+2)(x-4)+C(x+2)(x+3)$$
Quando usamos $latex x=-2$, temos:
$$ 9(-2)^2+34(-2)+14=A(-2+3)(-2-4)+B(-2+2)(-2-4)+C(-2+2)(-2+3)$$
$latex -18=-6A$
$latex A=3$
Quando usamos $latex x=-3$, temos:
$$ 9(-3)^2+34(-3)+14=A(-3+3)(-3-4)+B(-3+2)(-3-4)+C(-3+2)(-3+3)$$
$latex -7=7B$
$latex B=-1$
Quando usamos $latex x=4$, nós temos:
$$ 9(4)^2+34(4)+14=A(4+3)(4-4)+B(4+2)(4-4)+C(4+2)(4+3)$$
$latex 294=42C$
$latex C=7$
Então, temos:
$$\frac{9x^2+34x+14}{(x+2)(x+3)(x-4)}=\frac{3}{x+2}-\frac{1}{x+3}+\frac{7}{x-4}$$
Caso 2: Denominador com um factor quadrático irredutível
Cada fator quadrático da forma $latex (ax^2+bx+c)$ no denominador tem uma fração parcial correspondente da seguinte forma se for irredutível, ou seja, se não puder ser fatorado:
$$\frac{Ax+B}{ax^2+bx+c}$$
onde $latex a,~b,~c,~A$ e $latex B$ são constantes.
Por exemplo, suponha que temos a seguinte fração
$$\frac{7x^2+2x-28}{(x-6)(x^2+3x+5)}$$
As suas fracções parciais têm a seguinte forma:
$$\frac{7x^2+2x-28}{(x-6)(x^2+3x+5)}=\frac{A}{x-6}+\frac{Bx+C}{x^2+3x+5}$$
Então, podemos encontrar os valores de A, B e C usando os mesmos métodos vistos no caso I, como mostrado no exemplo a seguir.
EXEMPLO
Expresse a seguinte fração em frações parciais:
$$\frac{7x^2+2x-28}{(x-6)(x^2+3x+5)}$$
Solución
Como a expressão quadrática $latex x^2+3x+5$ no denominador não pode ser considerada, podemos assumir que as frações parciais têm a seguinte forma:
$$\frac{7x^2+2x-28}{(x-6)(x^2+3x+5)}=\frac{A}{x-6}+\frac{Bx+C}{x^2+3x+5}$$
Agora, multiplique a expressão inteira por $latex (x-6)(x^2+3x+5)$ e temos:
$$7x^2+2x-28=A(x^2+3x+5)+(Bx+C)(x-6)$$
Quando substituímos $latex x=6$, podemos encontrar o valor de A:
$$7(6)^2+2(6)-28=A((6)^2+3(6)+5)+(B(6)+C)(6-6)$$
$latex 236=59A$
$latex A=4$
Quando comparamos os coeficientes dos termos com $latex x^2$, temos:
$latex 7=A+B$
Substituindo $latex A=4$ nesta equação, obtemos o valor $latex B=3$.
Se agora compararmos os termos constantes, temos:
$latex -28=5A-6C$
Substituindo $latex A=4$ por esta equação, obtemos o valor $latex C=8$.
Então, as fracções parciais são:
$$\frac{7x^2+2x-28}{(x-6)(x^2+3x+5)}=\frac{4}{x-6}+\frac{3x+8}{x^2+3x+5}$$
Caso 3: Denominador com um factor repetido
Cada fator linear repetido da forma $latex (ax+b)^2$ no denominador tem frações parciais da seguinte forma:
$$\frac{A}{ax+b}+\frac{B}{ax+b}^2$$
onde $latex A,~b,~A$ e $latex B $ são constantes.
Por exemplo, suponha que temos a seguinte fração
$$\frac{2x^2+29x-1}{(2x+1)(x-2)^2}$$
Podemos decompor em frações parciais usando a seguinte forma:
$$\frac{2x^2+29x-1}{(2x+1)(x-2)^2}=\frac{A}{2x+1}+\frac{B}{x-2}+\frac{C}{(x-2)^2}$$
Encontramos os valores das constantes A, B e C aplicando as mesmas técnicas que nos casos anteriores.
EXEMPLO
Expresse a seguinte fração em frações parciais:
$$\frac{2x^2+29x-1}{(2x+1)(x-2)^2}$$
Solução
Esta fração tem um fator linear $latex (2x+1)$ e um fator repetido $latex (x-2)^2$. Então, as suas fracções parciais têm a forma:
$$\frac{2x^2+29x-1}{(2x+1)(x-2)^2}=\frac{A}{2x+1}+\frac{B}{x-2}+\frac{C}{(x-2)^2}$$
Agora, multiplique toda a expressão pelo denominador da fração original $latex (2x+1)(x-2)^2$ e temos:
$$2x^2+29x-11=A(x-2)^2+B(2x+1)(x-2)+C(2x+1)$$
Quando usamos o valor $latex x=-\frac{1}{2}$, temos:
$$2(-\frac{1}{2})^2+29(-\frac{1}{2})-11=A(-\frac{1}{2}-2)^2+B(2(-\frac{1}{2})+1)(-\frac{1}{2}-2)+C(2(-\frac{1}{2})+1)$$
$$-25=\frac{25}{4}A$$
$latex A=-4$
Quando usamos o valor $latex x=2$, temos:
$$2(2)^2+29(2)-11=A(2-2)^2+B(2(2)+1)(2-2)+C(2(2)+1)$$
$latex 55=5C$
$latex C=11$
Se compararmos os coeficientes dos termos com $latex x^2$, temos:
$latex 2=A+2B$
Usando o valor $latex A=-4$ nesta equação, encontramos o valor de $latex B=3$. Então, temos:
$$\frac{2x^2+29x-1}{(2x+1)(x-2)^2}=-\frac{4}{2x+1}+\frac{3}{x-2}+\frac{11}{(x-2)^2}$$
Caso 4: Fracções impróprias
Uma fração algébrica imprópria é uma fração na qual o grau do numerador é maior ou igual ao grau do denominador.
Para simplificar uma fração algébrica imprópria, podemos dividir o numerador pelo denominador. Quando fizermos isso, podemos obter o seguinte:
- Se um polinômio de grau $latex n$ é dividido por um polinômio de grau $latex n$, o quociente é uma constante.
- Se um polinômio de grau $latex n$ for dividido por um polinômio de grau $latex m$, onde $latex m<n$, o quociente é um polinômio de grau $latex (n-m)$.
Por exemplo, na fração seguinte o grau do numerador é 2 e o grau do denominador também é 2:
$$\frac{5x^2-71}{(x+5)(x-4)}$$
Então, o quociente é uma constante (a constante A) e as suas fracções parciais têm a seguinte forma:
$$\frac{5x^2-71}{(x+5)(x-4)}=A+\frac{B}{x+5}+\frac{C}{x-4}$$
Na fração seguinte, o grau do numerador é 4 e o grau do denominador é 3:
$$\frac{3x^4+7x^3+8x^2+53x-186}{(x+4)(x^2+9)}$$
Então, o quociente é um polinómio de grau (4-3)=1 e as suas fracções parciais têm a seguinte forma:
$$\frac{3x^4+7x^3+8x^2+53x-186}{(x+4)(x^2+9)}=Ax+B+\frac{C}{x+4}+\frac{Dx+E}{x^2+9}$$
EXEMPLO
Expresse a seguinte fração em frações parciais
$$\frac{5x^2-71}{(x+5)(x-4)}$$
Solução
O grau do polinômio no numerador é 2 e o grau do polinômio no denominador é também 2.
Então, o quociente é uma constante e as suas fracções parciais têm a seguinte forma:
$$\frac{5x^2-71}{(x+5)(x-4)}=A+\frac{B}{x+5}+\frac{C}{x-4}$$
Multiplique a expressão inteira por $latex (x+5)(x-4)$ e temos:
$$5x^2-71=A(x+5)(x-4)+B(x-4)+C(x+5)$$
Podemos encontrar o valor de A facilmente comparando os coeficientes dos termos com $latex x^2$ e descobrir que $latex A=5$.
Quando usamos o valor $latex x=-5$, temos:
$$5(-5)^2-71=B(-5-4)$$
$latex 54=-9B$
$latex B=-6$
Quando usamos o valor $latex x=4$, temos:
$$5(4)^2-71=C(4+5)$$
$latex 9=9C$
$latex C=1$
Então, temos:
$$\frac{5x^2-71}{(x+5)(x-4)}=5-\frac{6}{x+5}+\frac{1}{x-4}$$
→ Calculadora de frações parciais
Veja também
Interessado em saber mais sobre fracções parciais? Confira estas páginas: