As propriedades dos logaritmos, também conhecidas como regras dos logaritmos, são úteis porque nos permitem expandir, condensar ou resolver equações que contêm expressões logarítmicas.
A seguir, aprenderemos sobre as propriedades e regras dos logaritmos. Aprenderemos como derivar essas propriedades usando as regras dos expoentes. Além disso, veremos exemplos da aplicação dessas propriedades.
Propriedade do produto dos logaritmos
A regra do produto dos logaritmos indica que a multiplicação de dois ou mais logaritmos com a mesma base pode ser escrita como a soma dos logaritmos individuais:
Teste desta propriedade
Suponha que temos $latex x=\log_{b}(p)$ e $latex y=\log_{b}(q)$. Podemos escrever cada uma dessas equações em forma exponencial:
⇒ $latex {{b}^x}=p$
⇒ $latex {{b}^y}=q$
Multiplicando os termos exponenciais p e q, temos:
$latex {{b}^x}\times {{b}^y}=pq$
Como a base é comum, podemos aplicar a regra do produto dos expoentes para adicionar os expoentes e combinar a base:
$latex {{b}^{x+y}}=pq$
Tomando o logaritmo com base “b” de ambos os lados, temos:
$latex \log_{b}({{b}^{x+y}})=\log_{b}(pq)$
Aplicando a regra de potência de logaritmos (que veremos mais tarde), temos:
$latex (x+y)\log_{b}(b)=\log_{b}(pq)$
$latex (x+y)=\log_{b}(pq)$
Agora, substituímos os valores de x e y na equação obtida:
| $latex \log_{b}(p)+\log_{b}(q)=\log_{b}(pq)$ |
EXEMPLOS
- Aplicando a propriedade do produto para resolver a expressão $latex \log_{4}(8)+\log_{4}(32)$, temos:
$latex \log_{4}(8)+\log_{4}(32)=\log_{4}(8\times 32)$
$latex =\log_{4}(256)$
$latex =4$
- Resolvendo a expressão $latex \log(25)+\log(4)$, temos:
$latex \log(25)+\log(4)=\log(25\times 4)$
$latex =\log(100)$
$latex =2$
Propriedade do quociente dos logaritmos
A regra do quociente de logaritmos indica que a razão de dois logaritmos com as mesmas bases é igual à diferença dos logaritmos:
Teste desta propriedade
Vamos definir as equações $latex x=\log_{b}(p)$ e $latex y=\log_{b}(q)$. Então, podemos reescrevê-las em sua forma exponencial:
⇒ $latex {{b}^x}=p$
⇒ $latex {{b}^y}=q$
Se dividirmos os termos exponenciais p e q, temos:
$latex \frac{{{b}^x}} {{{b}^y}}=\frac{p}{q}$
Como a base é comum, aplicamos a regra do quociente do expoente para combinar a base e subtrair os expoentes:
$latex {{b}^{x-y}}=\frac{p}{q}$
Agora, podemos pegar o logaritmo com base “b” de ambos os lados:
$latex \log_{b}({{b}^{x-y}})=\log_{b}(\frac{p}{q})$
Se aplicarmos a regra de potência de logaritmos (que veremos mais tarde), temos:
$latex (x-y)\log_{b}(b)=\log_{b}(\frac{p}{q})$
$latex (x-y)=\log_{b}(\frac{p}{q})$
Se substituirmos os valores de x e y na equação obtida, temos:
| $latex \log_{b}(p)-\log_{b}(q)=\log_{b}(\frac{p}{q})$ |
EXEMPLOS
- Podemos resolver a expressão $latex \log_{5}(50)-\log_{5}(2)$ com a propriedade do quociente:
$latex \log_{5}(50)-\log_{5}(2)=\log_{5}(\frac{50}{2})$
$latex =\log_{5}(25)$
$latex =2$
- Se aplicarmos a propriedade do quociente a $latex \log_{3}(108)-\log_{3}(4)$, temos:
$latex \log_{3}(108)-\log_{3}(4)=\log_{3}(\frac{108}{4})$
$latex =\log_{3}(27)$
$latex =3$
Propriedade de potência dos logaritmos
De acordo com a propriedade da potência dos logaritmos, o logaritmo de um número “p” com expoente “n” é igual ao produto do expoente e o logaritmo do número (sem o expoente):
Teste desta propriedade
Vamos definir a equação $latex x=\log_{b}(p)$ e vamos escrevê-la em sua forma exponencial:
⇒ $latex {{b}^x}=p$
Podemos elevar à potência de n ambos os lados da equação:
$latex {{({{b}^x})}^n}={{p}^n}$
⇒ $latex {{b}^{xn}}={{p}^n}$
Se tomarmos o logaritmo com base “b” de ambos os lados, temos:
$latex \log_{b}({{b}^{xn}})=\log_{b}({{p}^n})$
$latex xn\log_{b}(b)=\log_{b}({{p}^n})$
$latex xn=\log_{b}({{p}^n})$
Substituindo o valor de x na equação obtida, temos:
| $latex n\log_{b}(p)=\log_{b}({{p}^n})$ |
EXEMPLOS
- Resolvemos a expressão $latex \log_{8}({{64}^2})$ aplicando a propriedade de potência de logaritmos:
$latex \log_{8}({{64}^2})=2\log_{8}(64)$
$latex =2(2)$
$latex =4$
- Aplicando a propriedade de potência na expressão $latex \log({{100}^4})$, temos:
$latex \log({{100}^4})=4\log(100)$
$latex =4(2)$
$latex =8$
Propriedade de mudança de base dos logaritmos
De acordo com a propriedade de mudança de base do logaritmo, podemos reescrever qualquer logaritmo como a proporção de dois logaritmos com uma nova base:
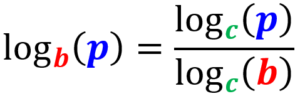
Teste desta propriedade
Suponha que temos $latex x=\log_{b}(p)$. Podemos escrever isso em sua forma exponencial:
⇒ $latex {{b}^x}=p$
Aplicando o logaritmo com base “c” em ambos os lados, temos:
$latex \log_{c}({{b}^{x}})=\log_{c}(p)$
Usamos a regra de potência de logaritmos:
$latex (x)\log_{c}(b)=\log_{c}(p)$
Agora, podemos resolver para x:
$latex x=\frac{\log_{c}(p)}{\log_{c}(b)}$
Agora, substituímos o valor de x:
| $latex \log_{b}(p)=\frac{\log_{c}(p)}{\log_{c}(b)}$ |
EXEMPLOS
- Aplicamos a propriedade de mudança de bases para resolver $latex \log_{8}(16)$:
$latex \log_{8}(16)=\frac{\log_{2}(16)}{\log_{2}(8)}$
$latex =\frac{4}{3}$
- Resolvendo a expressão $latex \log_{27}(81)$, temos:
$latex \log_{27}(81)=\frac{\log_{3}(81)}{\log_{3}(27)}$
$latex =\frac{4}{3}$
Outras propriedades
- O logaritmo de 1 para qualquer base finita diferente de zero é igual a zero.
Teste desta propriedade
Podemos provar isso reescrevendo-a em sua forma exponencial:
$latex \log_{b}(1)=0$
⇒ $latex {{b}^0}=1$
- O logaritmo de qualquer número positivo para a mesma base é igual a 1.
Teste desta propriedade
Novamente, podemos provar isso reescrevendo-a em sua forma exponencial:
$latex \log_{b}(b)=1$
⇒ $latex {{b}^1}=b$
Veja também
Você quer aprender mais sobre logaritmos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
