Propriedades do triângulo de Pascal

Definição do triângulo de Pascal

O triângulo de Pascal pode ser introduzido através de um conjunto de regras. Para formar o triângulo de Pascal, começamos com 1 no topo e colocamos “1” ao longo de ambos os lados do triângulo.

Cada novo número ficará entre e abaixo de dois números, e seu valor é igual à soma desses dois números. O triângulo teórico é infinito e pode continuar indefinidamente enquanto for necessário.

Construção do triângulo de Pascal

As linhas no triângulo de Pascal são numeradas começando em 0, então a linha superior é a linha 0. A maneira mais fácil de construir um triângulo de Pascal é começar da linha zero e escrever apenas o número 1.

A partir daí, obtemos cada número na próxima linha adicionando os dois números diretamente no canto superior esquerdo e direito. Se não houver nenhum número à direita ou à esquerda, substituímos esse número por zero e prosseguimos com a adição.

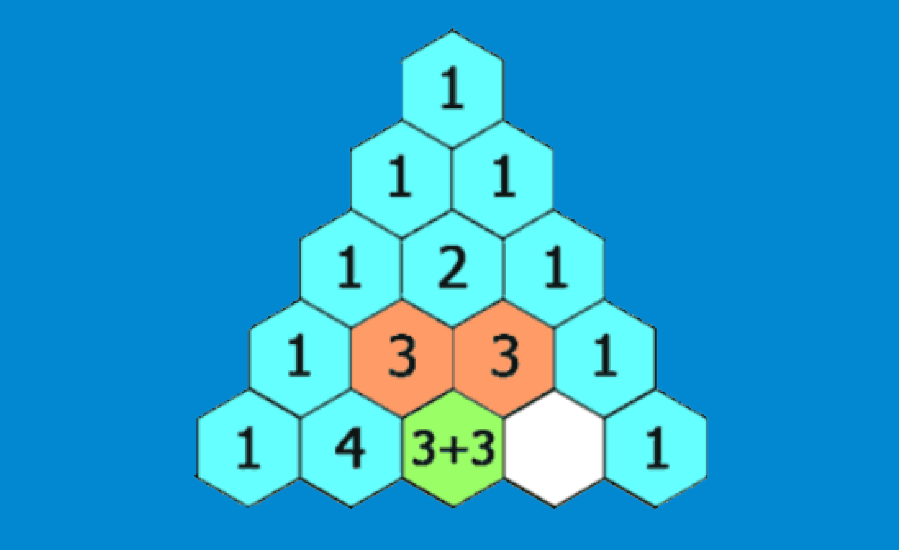
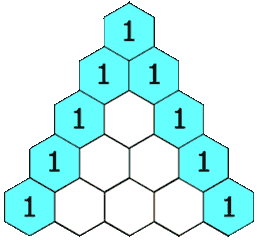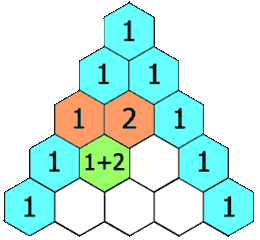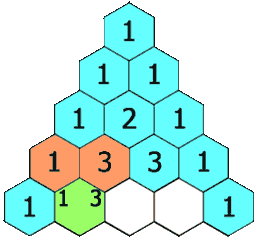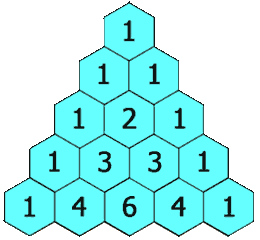
O seguinte é uma ilustração de como construir o triângulo de Pascal:

Propriedades do triângulo de Pascal

A seguir estão as propriedades mais importantes do triângulo de Pascal:

• Cada número é a soma dos dois números acima dele.
• Todos os números externos são iguais a 1.
• O triângulo de Pascal é simétrico.
• A primeira diagonal mostra os números contados.
• As somas das linhas dão as potências de 2.
• Cada linha dá os dígitos das potências de 11.
• Cada elemento representa a combinação $latex{m}C_{n}$, onde m é a linha do elemento e n é a posição do elemento na linha.
• Cada linha representa os coeficientes binomiais.
• Os números de Fibonacci estão ao longo das diagonais.

Padrões de triângulo de Pascal

Soma das linhas

Uma das propriedades interessantes do triângulo é que a soma dos números em uma linha é igual a $latex {{2}^n}$, onde n é o número na linha. Por exemplo, temos:

• $latex 1=1={{2}^0}$
• $latex 1+1=2={{2}^1}$
• $latex 1+2+1=4={{2}^2}$
• $latex 1+3+3+1=8={{2}^3}$
• $latex 1+4+6+4+1=16={{2}^4}$

Números primos no triângulo

Outro padrão visível no triângulo está relacionado aos números primos. Se uma linha começa com um número primo ou é uma linha de número primo, todos os números nessa linha, exceto 1, são divisíveis por esse número primo.

Se olharmos para a linha 5 (1, 5, 10, 10, 5, 1) podemos ver que 5 e 10 são divisíveis por 5. No entanto, para uma linha composta como a linha 8 (1, 8, 28, 56, 70 , 56, 28, 8, 1), 28 e 70 não são divisíveis por 8.

Sequência de Fibonacci no triângulo

Somando os números nas diagonais do triângulo de Pascal, podemos obter a sequência de Fibonacci, conforme mostra a figura:

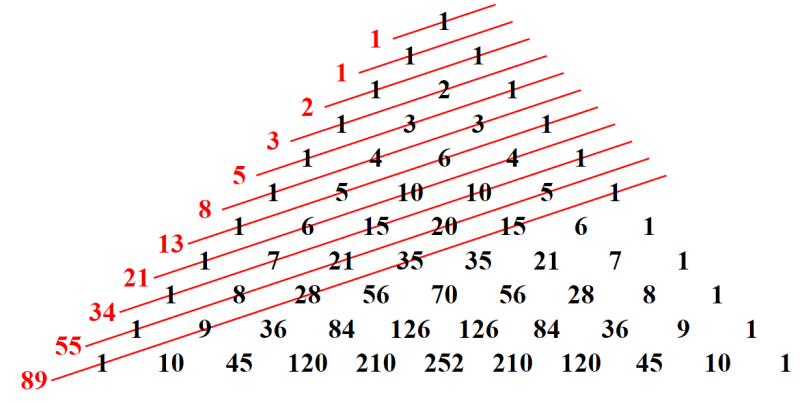
Expansão binomial com triângulo de Pascal

O triângulo de Pascal define os coeficientes que aparecem em expressões binomiais. Isso significa que a linha n do triângulo de Pascal contém os coeficientes da expressão binomial expandida $latex {{(x+y)}^n}$.

Os coeficientes de expansão podem ser expressos como $latex a_{k}=_{n}C_{k}$. Por exemplo, podemos expandir a expressão para o binômio $latex {{x+y}^3}$:

$${{(x+y)}^3}=_{3}C_{0}{{x}^3}+_{3}C_{1}{{x}^2}y+_{3}C_{2}x{{y}^2}+_{3}C_{3}{{y}^3}$$

$latex =(1){{x}^3}+(3){{x}^2}y+(3)x{{y}^2}+(1){{y}^3}$

Nesta expressão, temos $latex n=3$, o que significa que usamos os números da linha 3 do triângulo de Pascal, que são 1, 3, 3, 1.

Veja também

Interessado em aprender mais sobre o triângulo de Pascal e o teorema binomial? Veja estas páginas:

• Aplicações do triângulo de Pascal
• Binómio de Newton com Exercícios