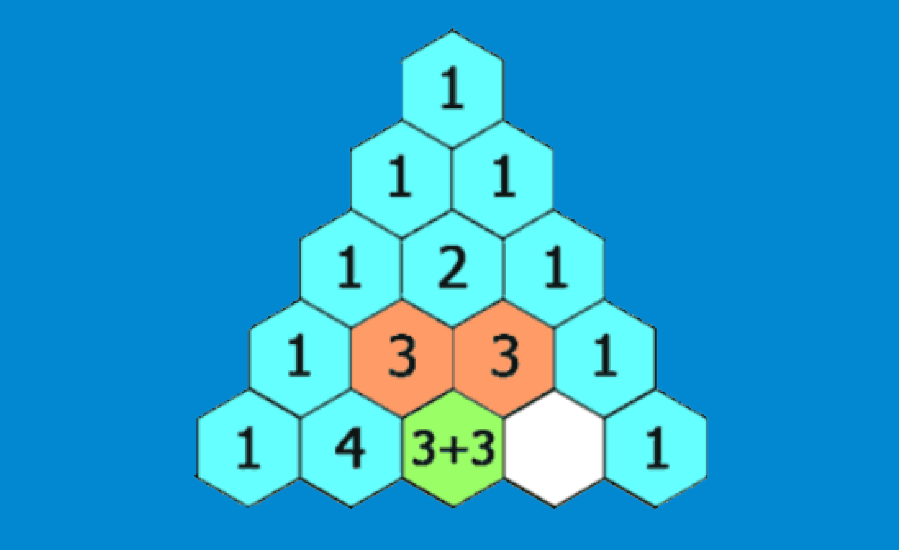
O triângulo de Pascal tem muitas aplicações em matemática e estatística. Podemos usar o triângulo de Pascal para encontrar a expansão binomial. Além disso, o triângulo de Pascal é usado em aplicações probabilísticas e no cálculo de combinações. Lembre-se de que o triângulo de Pascal é um padrão de números em forma de triângulo, onde cada número é encontrado somando os dois números acima dele.
A seguir, veremos cada uma das aplicações mais importantes do triângulo de Pascal em detalhes, juntamente com alguns exemplos para entender seu uso.
Triângulo de Pascal em expansão binomial
O seguinte é o triângulo de Pascal:
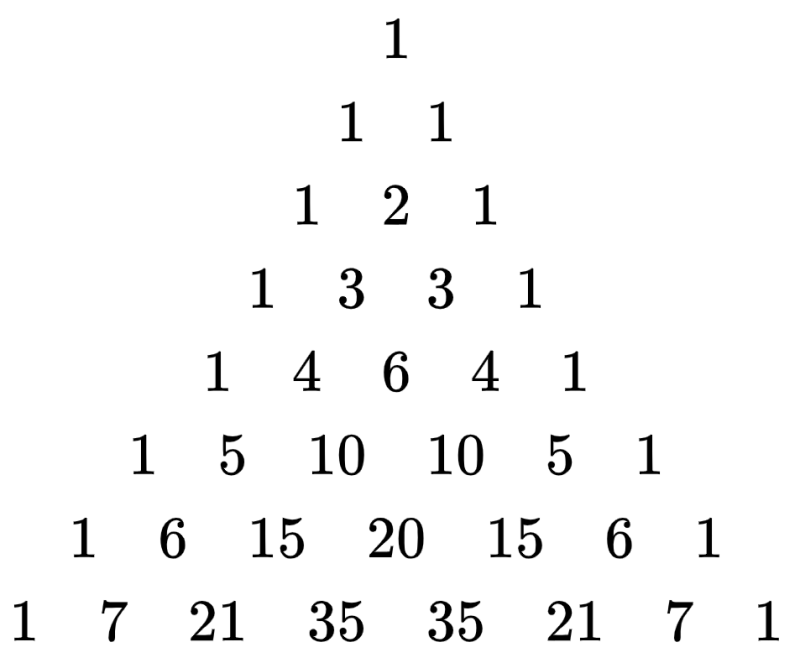
Podemos usar as linhas do triângulo de Pascal para facilitar o processo de expansão binomial. Conforme a potência do binômio, podemos usar uma linha do triângulo de Pascal que representa os coeficientes dos valores expandidos. Usamos n+1 para determinar a linha a ser usada, onde n representa a potência do binômio.
Alternativamente, podemos tomar a primeira linha como 0 e pegar a linha do triângulo de Pascal indicada pela potência. Por exemplo, vejamos a seguinte expansão binomial:
$latex {{(a+b)}^2}=1{{a}^2}+2ab+1{{b}^2}$
Nesta expansão, temos os coeficientes 1, 2, 1. Isso corresponde à terceira linha do triângulo de Pascal. Vemos que a potência do binômio é 2, então, usando n+1, temos 3 que corresponde à terceira linha usada.
EXEMPLO
- Expanda o binômio $latex {{(x+y)}^4}$.
Solução: Neste caso a potência é 4, então temos que usar a linha $latex 4+1=5$. Esta linha corresponde aos números 1, 4, 6, 4, 1. Estes são os coeficientes da expansão binomial e nos diz que teremos 5 termos na expansão. Além disso, sabemos que expandimos um binômio começando com cada termo na potência mais alta e reduzindo a 0, cada termo na direção oposta:
$latex {{(x+y)}^4}$
$$=1{{x}^4}{{y}^0}+4{{x}^3}{{y}^1}+6{{x}^2}{{y}^2}+4{{x}^1}{{y}^3}+1{{x}^0}{{y}^4}$$
$$=1{{x}^4}(1)+4{{x}^3}{{y}^1}+6{{x}^2}{{y}^2}+4{{x}^1}{{y}^3}+1(1){{y}^4}$$
$latex ={{x}^4}+4{{x}^3}y+6{{x}^2}{{y}^2}+4x{{y}^3}+{{y}^4}$
Triângulo de Pascal em probabilidade
O triângulo de Pascal pode ser usado em probabilidade para simplificar a contagem das probabilidades de algum evento. Por exemplo, o triângulo de Pascal pode nos mostrar de quantas maneiras podemos combinar cara e coroa no lançamento de moedas.
Então isso pode nos mostrar a probabilidade de qualquer combinação. No exemplo a seguir, S representa coroa e C representa cara.
EXEMPLO
Suponha que uma moeda seja lançada 4 vezes, as probabilidades das combinações são:
- CCCC
- CCCS, CCSC, CSCC, SCCC
- CCSS, CSCS, CSSC, SCCS, SCSC, SSCC
- CSSS, SCSS, SSCS, SSSC
- SSSS
Assim, o padrão observado é 1, 4, 6, 4, 1. Se estivermos procurando o número total de possibilidades, apenas somamos os números. Ou seja, temos $latex 1+4+6+4+1=16$ combinações possíveis se jogarmos uma moeda 4 vezes.
Triângulo de Pascal em combinações
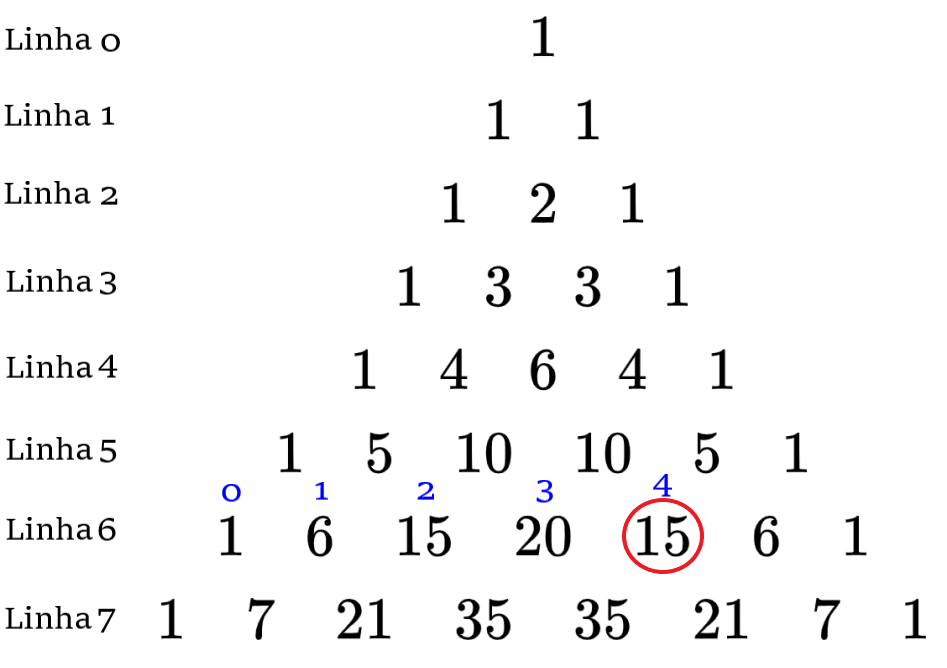
O triângulo de Pascal pode ser usado para encontrar combinações. A linha superior do triângulo de Pascal é a linha 0, e o primeiro número em cada linha é o elemento zero dessa linha.
Por exemplo, se quisermos encontrar a combinação $latex _{6}C_{4}$, temos que olhar a linha 6 e o item 4. A resposta é 15:
EXEMPLO
- Temos 5 bolinhas de gude em um saco, 1 vermelha, 1 azul, 1 verde, 1 amarela e 1 preta. Quantas combinações são possíveis se quisermos obter 2 bolinhas de gude?
Soluções: O número total de bolinhas é 5 e queremos escolher 2 bolinhas. Então, temos a combinação $latex _{5}C_{2} $. Isso significa que precisamos olhar para o 2º item na linha 5. Isso significa que a resposta é 10.
Veja também
Interessado em aprender mais sobre o triângulo de Pascal e o teorema binomial? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
