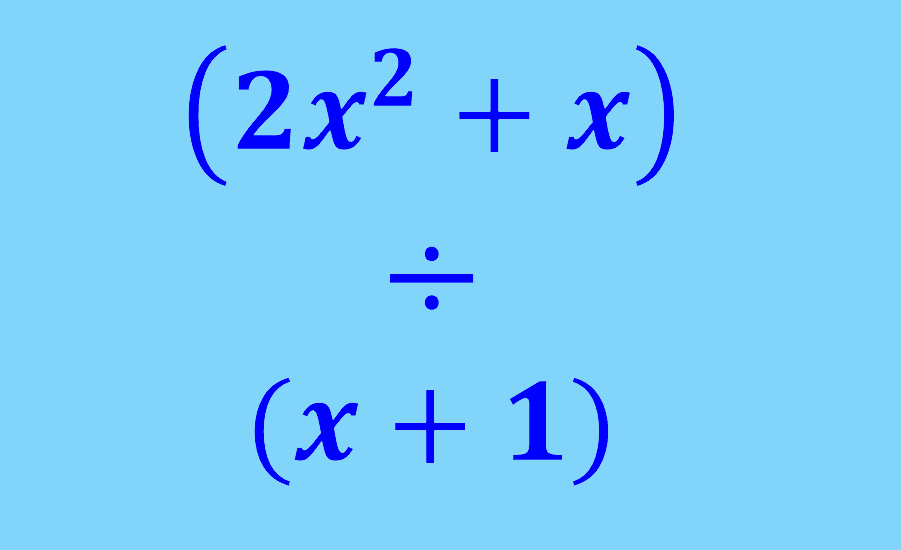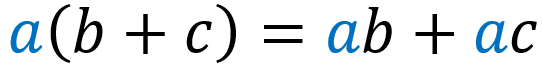Podemos realizar várias operações com expressões algébricas. Essas operações incluem adição, subtração, multiplicação e divisão. A seguir, aprenderemos a realizar essas operações com expressões algébricas. Veremos vários exemplos elaborados para compreender totalmente as idéias principais.
ALGEBRA
Relevante para…
Realizar adição, subtração, multiplicação e divisão com expressões algébricas.
ALGEBRA
Relevante para…
Realizar adição, subtração, multiplicação e divisão com expressões algébricas.
Ordem de operações
As operações com expressões algébricas seguem uma certa ordem. Cada vez que você vir uma expressão algébrica ou uma equação, decomponha-a na ordem em que deve ser resolvida. Para lembrar facilmente esta ordem, considere este acrônimo: PEMDAS:
1. Avalie todas as expressões entre parênteses ou outros símbolos de agrupamento.
2. Avalie todas as expressões que contêm expoentes.
3. Faça as multiplicações e divisões restantes à medida que as encontrar. Ou seja, faça as multiplicações e divisões da esquerda para a direita.
4. Faça as adições e subtrações restantes à medida que as encontrar. Ou seja, some e subtraia da esquerda para a direita.
EXERCÍCIOS
- Resolva $latex 5+4\times 3$.
Solução: Aplicar a ordem das operações:
$latex 5+4\times 3=5+12=17$
- Resolva $latex 2\left( {3+1} \right)+2\times 3\left( {3+1} \right)$.
Solução:Aplicar a ordem das operações:
$$2\left( {3+1} \right)+2\times 3\left( {3+1} \right)=2\left( 4 \right)+2\times 3\left( 4 \right)$$
$latex =8+2\times 12$
$latex =8+24$
$latex =32$
Experimente você mesmo – Resolva os exercícios
Adição e subtração
Ao adicionar ou subtrair expressões algébricas, é importante que os termos sejam termos semelhantes. Termos semelhantes são definidos como as mesmas variáveis elevadas à mesma potência.
EXERCÍCIOS
- Adicione as expressões $latex 2x+4$ e $latex 3x+2$.
Solução: Identifique os termos semelhantes e combine-os:
$latex 2x+4+3x+2=5x+6$
- Adicione as expressões $latex 2{{x}^{2}}+3x+4$ e $latex 4{{x}^{2}}-2x+3$ .
Solução: Identifique os termos semelhantes e combine-os:
$latex 2{{x}^{2}}+3x+4+4{{x}^{2}}-2x+3$
$latex =6{{x}^{2}}+x+7$
- Subtraia a expressão $latex 3x+3$ da expressão $latex 8x+5$.
Solução: Por ser uma subtração, mudamos o sinal da expressão que está subtraindo:
$$8x+5-(3x+3)=8x+5-3x-3$$
$latex =5x+2$
- Subtraia a expressão $latex 2{{x}^{2}}+3x-6$ da expressão $latex -4{{x}^{2}}+2x-5$.
Solução: Por ser uma subtração, mudamos o sinal da expressão que está subtraindo:
$latex -4{{x}^{2}}+2x-5-\left( {2{{x}^{2}}+3x-6} \right)$
$latex =-4{{x}^{2}}+2x-5-2{{x}^{2}}-3x+6$
$latex =-6{{x}^{2}}-x+1$
Experimente você mesmo – Resolva os exercícios
Multiplicação
Para multiplicar expressões algébricas, temos que usar a propriedade distributiva. A propriedade distributiva indica que para quaisquer números reais a, b, c, temos:
EXERCÍCIOS
- Multiplique $latex x$ por $latex x+1$.
Solução: Usamos a propriedade distributiva para distribuir o $latex x$:
$latex x\left( {x+1} \right)=x\times x+x\times 1$
$latex ={{x}^{2}}+x$
- Multiplique $latex x+2$ por $latex x+1$.
Solução: Usamos a propriedade distributiva duas vezes, distribuímos $latex x$ e depois 2:
$$(x+2)(x+1)={{x}^{2}}+x+2x+2$$
$latex ={{x}^{2}}+3x+2$
- Multiplique $latex x+4$ por $latex {{x}^{2}}+2x-5$.
Solução: Usamos a propriedade distributiva duas vezes, distribuímos $latex x$ e depois 4:
$latex (x+4)({{x}^{2}}+2x-5)$
$$={x}^{3}+2{{x}^{2}}-5x+4{{x}^{2}}+8x-20$$
$latex ={{x}^{3}}+6{{x}^{2}}+3x-20$
- Multiplique $latex x-3$ por $latex 2{{x}^{2}}-2x+3$.
Solução: Usamos a propriedade distributiva duas vezes, distribuímos $latex x$ e depois -3:
$latex (x-3)(2{{x}^{2}}-2x+3)$
$$=2{x}^{3}-2{{x}^{2}}+3x-6{{x}^{2}}+6x-9$$
$latex ={2{x}^{3}}-8{{x}^{2}}+9x-12$
Experimente você mesmo – Resolva os exercícios
Divisão
Dividir uma expressão algébrica é semelhante a simplificar os termos. Os coeficientes numéricos são divididos e os expoentes das variáveis são subtraídos.
EXERCÍCIOS
- Divida $latex 6{{a}^{2}}{{b}^{3}}$ por $latex 2{{a}^{3}}{{b}^{2}}$.
Solução: Para entender mais facilmente, escrevemos a divisão da seguinte forma:
$$\frac{{6aa~bbb}}{{2~aaa~bb}}$$
Dividimos as constantes e simplificamos as variáveis:
$$=\frac{{3b}}{a}$$
- Resolva o seguinte:
$$\frac{{\left( {x+1} \right)\left( {x+2} \right)}}{{\left( {x+2} \right)\left( {x-3} \right)}}$$
Solução: Simplificamos a expressão algébrica cancelando os termos:
$$\frac{{x+1}}{{x-3}}$$
- Simplifique a expressão $latex \frac{3}{x}+\frac{4}{{x+1}}$.
Solução: Para simplificar, a equação precisa ter o mesmo denominador. Aqui, multiplicamos ambos os termos por $latex x\left( {x+1} \right)$ e cancelamos:
$$\frac{{3\left( x \right)\left( {x+1} \right)}}{x}=3\left( {x+1} \right)$$
$$\frac{{4\left( x \right)\left( {x+1} \right)}}{{x+1}}=4x$$
Unindo os termos e simplificando, temos:
$$3\left( {x+1} \right)+4x=3x+3+4x$$
$latex =7x+3$
Experimente você mesmo – Resolva o exercício
Veja também
Você quer aprender mais sobre expressões algébricas ? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
