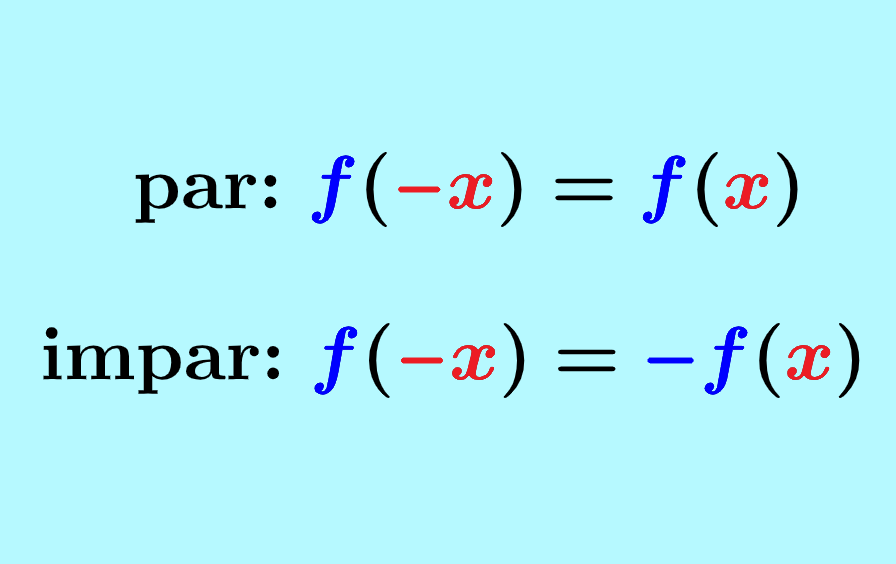As funções ímpares e pares são duas funções com características importantes. Uma função par exibe simetria em torno do eixo y. Por outro lado, a função ímpar tem simetria rotacional de 180° em relação à origem. É possível determinar se uma função é ímpar ou par usando métodos algébricos.
A seguir, aprenderemos tudo sobre as funções pares e ímpares. Veremos seus gráficos, algumas características importantes e conheceremos como determinar se uma função é par ou ímpar.
Características e gráfico da função par
Funções par têm a principal característica de serem simétricas em relação ao eixo y. Isso significa que, se dobrarmos o gráfico no eixo y, obteremos duas partes iguais do gráfico.
Uma função par importante é a função $latex f(x)=x^2$, que tem o seguinte gráfico:
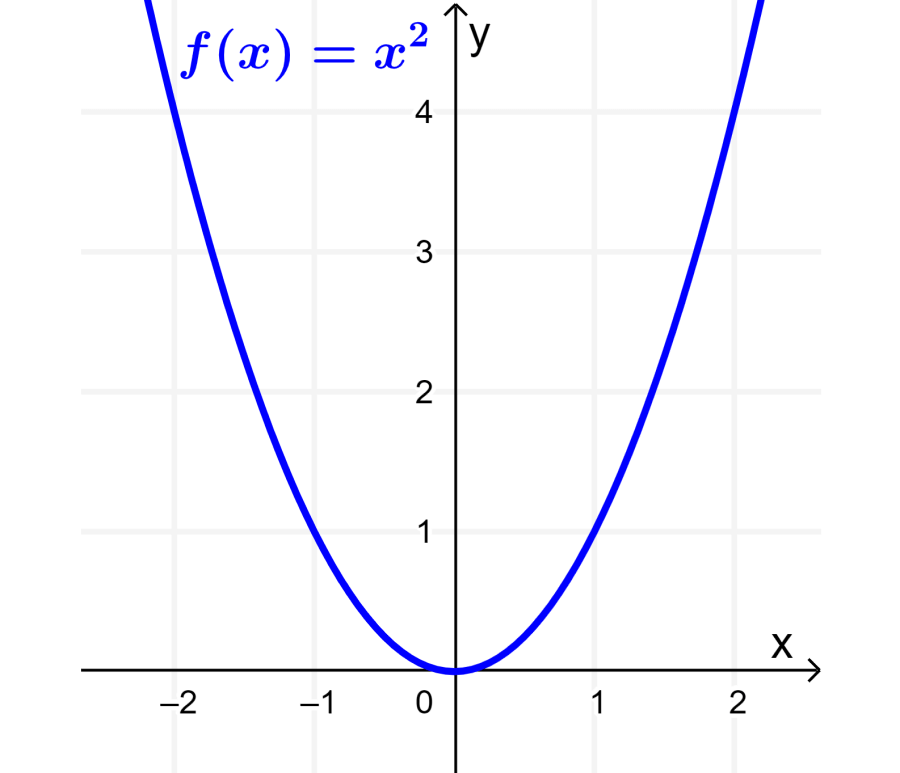
Outros exemplos de funções pares são as seguintes funções:
- $latex f(x)=\cos(x)$
- $latex f(x)=x^4$
- $latex f(x)=\sin^2(x)$
Fórmula de funções pares
Para determinar se uma função é par ou não, podemos usar a seguinte fórmula:
$latex f(-x)=f(x)$
Isso significa que se substituir os valores de x na função por –x nos der a função original, então a função é par.
Características e gráfico da função ímpar
A principal característica das funções ímpares é que elas têm simetria rotacional de 180° em relação à origem. Isso significa que se girarmos o gráfico 180° em torno do ponto (0, 0), o gráfico não mudará.
Uma função ímpar importante é a função $latex f(x)=x^3$, que tem o seguinte gráfico:
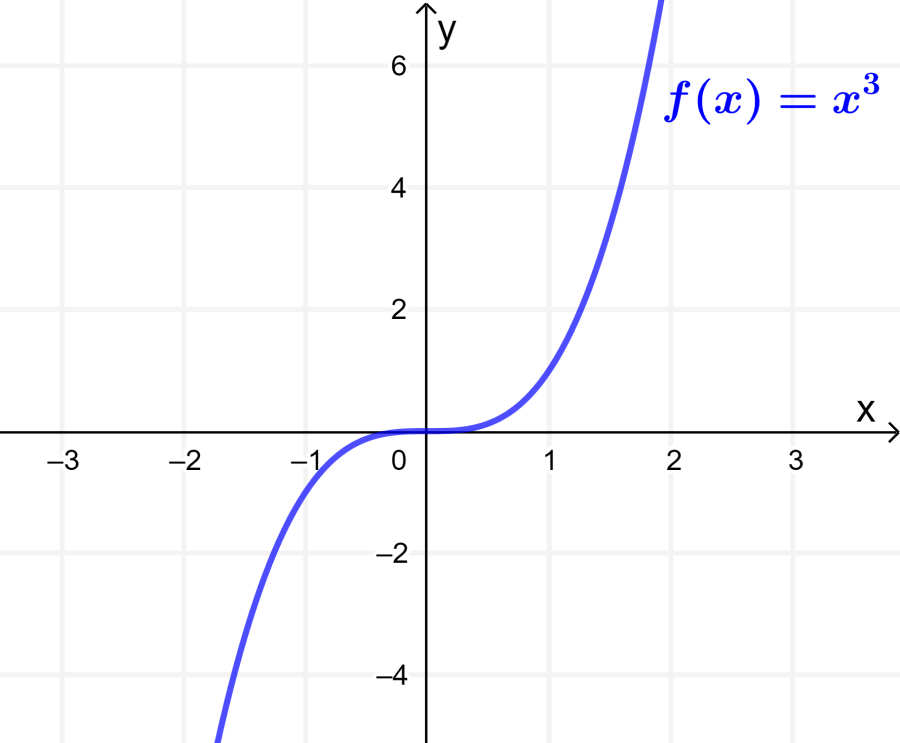
Outros exemplos de funções ímpares são as seguintes funções:
- $latex f(x)=\sin(x)$
- $latex f(x)=x^5$
- $latex f(x)=x^7$
Fórmula de funções ímpares
Podemos determinar se uma função é par ou ímpar usando a seguinte fórmula:
$latex f(-x)=-f(x)$
Isso significa que se substituir os valores de x na função por –x nos der a função original multiplicada por -1, então a função é ímpar.
Exemplos de funções pares e ímpares
Nos exemplos a seguir, podemos aplicar o que aprendemos sobre a imagem de uma função. Cada um dos exemplos tem uma solução detalhada usando o gráfico da função.
EXEMPLO 1
Determina se a função $latex f(x)={{x}^2}+1$ é par ou ímpar.
Solução: Para uma função ser par, a condição $latex f(-x)=f(x)$ deve ser verdadeira. Então, vamos verificar isso:
$latex f(-x)= (-x)^2+1$
$latex f(-x)= x^2+1$
Vemos que obtivemos a função original. Então a função é par. O seguinte é seu gráfico e podemos verificar que ele é par, pois é simétrico em relação ao eixo y.
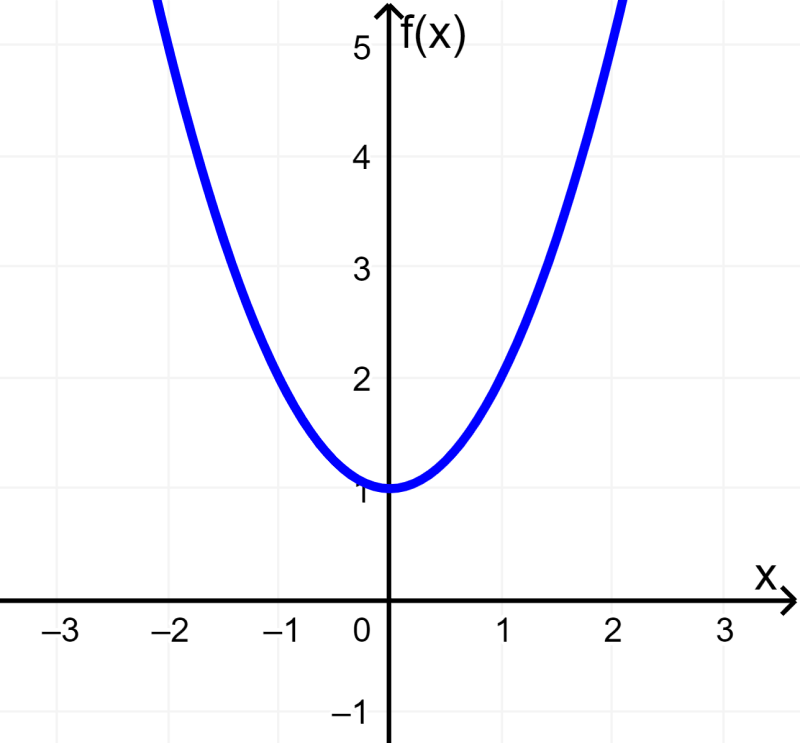
EXEMPLO 2
A função $latex f(x)=3x^2-|x|$ é par ou ímpar?
Solução: Podemos determinar se a função é par ou ímpar testando $latex f(-x)=f(x)$ para funções pares e $latex f(-x)=-f(x)$ para funções ímpares.
Começando com a prova de funções pares, temos:
$latex f(-x)=3(-x)^2-|-x|$
$latex f(-x)=3x^2-|x|$
Vemos que a expressão obtida é igual à função original $latex f(x)$, então a função é par.
Como a função é par, não precisamos mais testar funções ímpares.
EXEMPLO 3
Determine se a função $latex f(x)=\frac{3}{x}+2x$ é par ou ímpar.
Solução: Para resolver este problema, podemos aplicar o teste para funções pares e depois realizar o teste para funções ímpares.
Se a função for par, devemos ter $latex f(-x)=f(x)$. Então temos:
$latex f(-x)=\frac{3}{-x}+2(-x)$
$latex f(-x)=-\frac{3}{x}-2x$
Esta função não é par porque a expressão obtida não é igual à função original $latex f(x)$.
Observando a expressão obtida, vemos que ela é igual a $latex -f(x)$. Isso significa que a função é porque $latex f(-x)=-f(x)$.
EXEMPLO 4
A função $latex f(x)=(x^3-5)^2$ é par, ímpar ou nenhuma?
Solução: Usando a prova de funções pares, $latex f(-x)=f(x)$, temos:
$latex f(-x)=((-x)^3-5)^2$
$latex f(-x)=(-x^3-5)^2$
A expressão que obtivemos não é igual a $latex f(x)$, então a função não é par. Então, continuamos com a prova de funções ímpares.
Para verificar se a função é ímpar, devemos ter $latex f(-x)=-f(x)$. No entanto, a função também não é ímpar, pois a expressão obtida acima não é igual a $latex -f(x)$.
Nota: $latex -f(x)$ seria igual a $latex -(x^3-5)^2$.
Veja também
Interessado em aprender mais sobre funções algébricas? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
