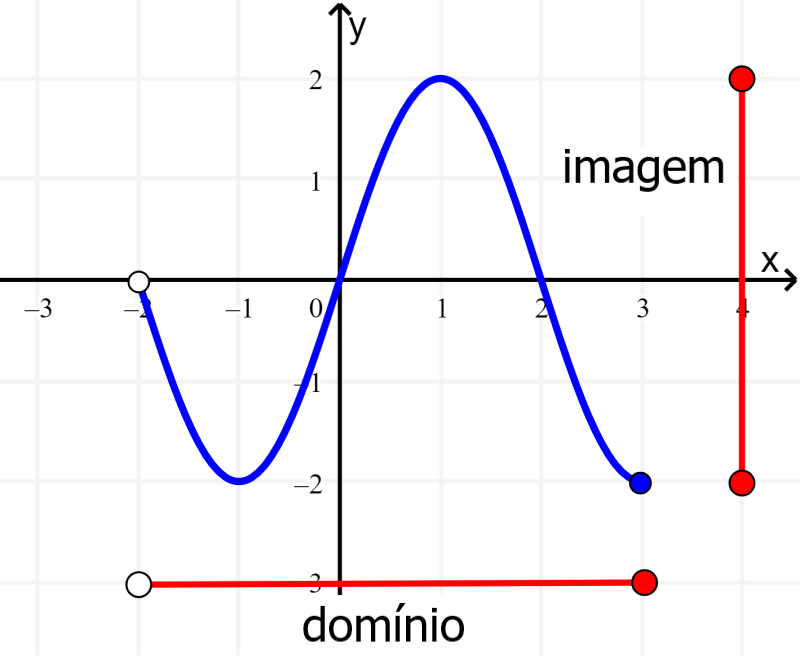
A imagem de uma função pode ser encontrada fazendo um gráfico da função e identificando todos os valores de y que são possíveis com o domínio da função. Em algumas funções, como funções lineares, funções cúbicas ou a função tangente, a imagem da função é igual a todos os números reais.
A seguir, aprenderemos como encontrar a imagem de uma função usando seu gráfico. Veremos alguns exemplos para ilustrar o processo utilizado.
Método para encontrar a imagem de uma função
Para encontrar a imagem de uma função, é sempre útil desenhar um gráfico simples da função. Por exemplo, suponha que temos a função $latex f(x)=2x$, que é definida para todos os valores reais de x. Assim, segue o seu gráfico:
A imagem da função $latex f(x)$ é o conjunto de todos os valores de saída da função. Ou seja, o intervalo é a parte do eixo y que é usada pela função. Nesta função, a imagem é o conjunto de todos os números reais.
Para indicar que a imagem são todos os números reais, podemos escrever
{$latex f(x):f(x)\in \mathbb{R}$}
ou simplesmente, podemos escrever $latex f(x) \in \mathbb{R}$.
Quando uma função é definida por um domínio restrito, a imagem da função também pode ser restrito. Por exemplo, considere a seguinte função e seu gráfico:
$latex f(x)=2x$, $latex ~~-1<x<4$
A imagem da função é o conjunto dos números reais de -2 a 8, excluindo -2 e 8, pois -1 e 4 são excluídos do domínio da função. Escrevemos este intervalo como
$latex -2<f(x)<8$
Exemplos de imagem de funções
Nos exemplos a seguir, podemos aplicar o que aprendemos sobre a imagem de uma função. Cada um dos exemplos tem uma solução detalhada usando o gráfico da função.
EXEMPLO 1
Encontre a imagem da função $latex f(x)={{x}^2}+1$.
Solução: A função $latex f(x)={{x}^2}+1$ é definida para todos os valores reais de x, pois não há restrições quanto ao valor de x. Seu gráfico é o seguinte:
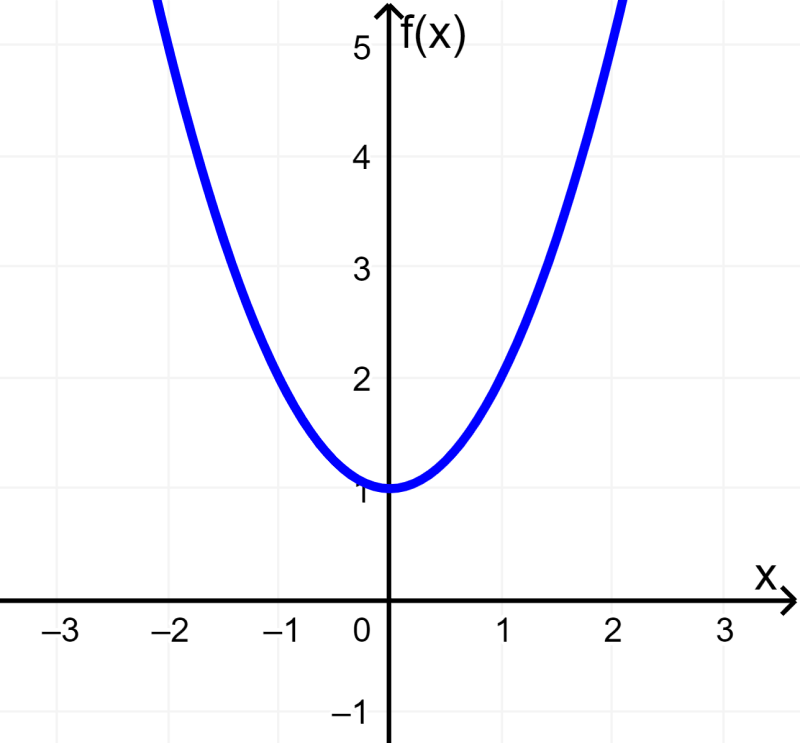
Como $latex {{x}^2}$ nunca é negativo, $latex {{x}^2}+1$ nunca é menor que 1. Portanto, a imagem de $latex f(x)$ é:
“Todos os números reais $latex f(x) \geq 1$”
O gráfico indica claramente que os valores de f(x) nunca são inferiores a 1.
EXEMPLO 2
Encontre a imagem da função $latex f(t)=\sqrt{5-t}$.
Solução: Esta é uma função de raiz quadrada. Seu gráfico é o seguinte:
Podemos ver que a função $latex f(t)$ não resulta em valores negativos. Então sua imagem é:
“Todos os números reais, $latex f(t)\geq 0$”
A imagem são todos os números reais maiores ou iguais a 0.
EXEMPLO 3
Qual é a imagem da função $latex f(x)=2x-1$, para $latex x\geq 0$.
Solução: Neste caso, a função $latex f(x)$ tem os valores de x restritos a números iguais ou maiores que 0. Assim, temos o seguinte gráfico:
A partir do gráfico, podemos ver que quando $latex x\geq 0$, temos $latex f(x)\geq -1$. Assim, a imagem da função é:
“Todos os números reais, $latex f(x)\geq -1$”
EXEMPLO 4
Encontre a imagem da função $latex f(x)= \frac{1}{x+3}$.
Solução: Esta é uma função racional que tem o seguinte gráfico:
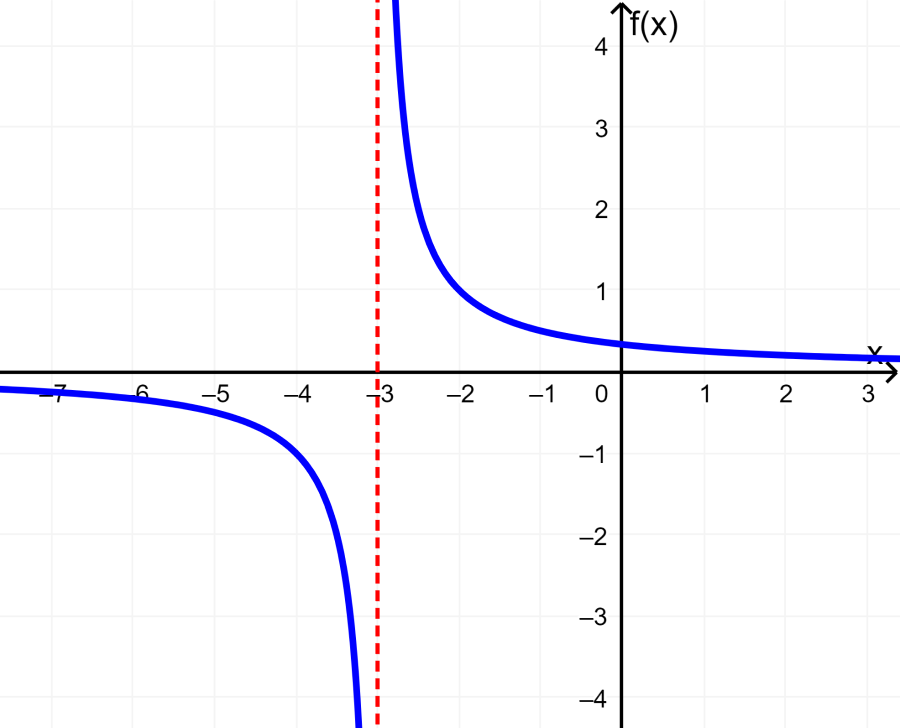
A função $latex f(x)= \frac{1}{x+3}$ não está definida para $latex x=-3$ porque isso resultaria na divisão por zero (teríamos um 0 no denominador).
A partir do gráfico, podemos ver que os valores de $latex f(x)$ podem ser qualquer valor, exceto zero. Se tentarmos resolver a equação para y = 0, temos:
$latex 0= \frac{1}{x+3}$
Multiplicando ambos os lados por $latex x+3$, temos:
$latex 0= 1$
Isto é impossível. Portanto, a imagem de $latex f(x)$ é:
“Todos os números reais, exceto zero”
Veja também
Interessado em aprender mais sobre funções algébricas? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
