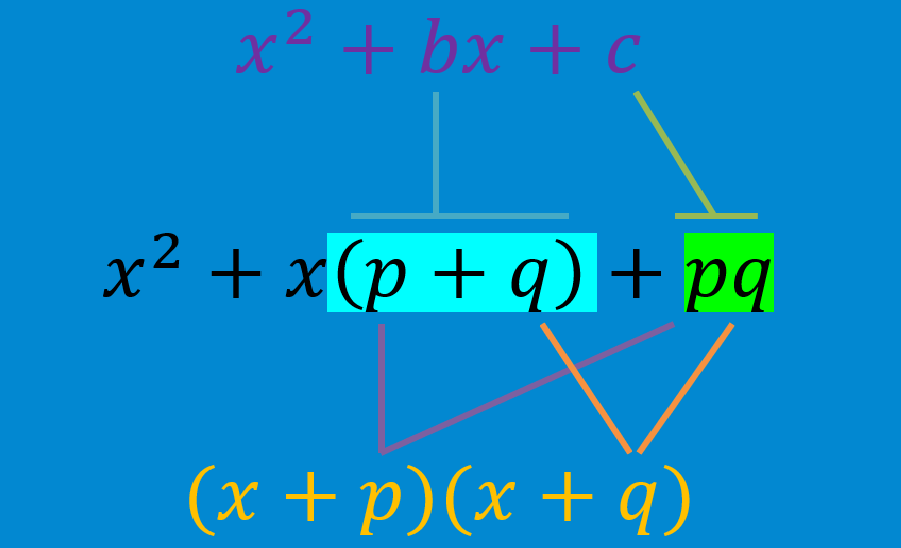Fatorar equações quadráticas consiste em decompor a equação quadrática e formar um produto de seus fatores. A fatoração pode ser considerada como o processo reverso da distribuição da multiplicação.
A seguir, aprenderemos sobre dois casos de fatoração de equações quadráticas. O primeiro caso é sobre equações quadráticas com um coeficiente líder de 1 e o segundo caso é sobre equações quadráticas com um coeficiente líder maior que 1.
Fatorando equações quadráticas quando o coeficiente de x² é igual a 1
Este é o caso mais fácil de fatorar equações quadráticas. Para fatorar equações quadráticas da forma $latex {{x}^2}+bx+c$, onde o coeficiente líder é 1, temos que encontrar dois números para que, ao multiplicá-los, obtenhamos a constante c e ao adicioná-los, obtenhamos o coeficiente b.
Primeiro caso: Quando b e c são ambos positivos
EXEMPLO 1
Fatore e subtraia a solução da equação quadrática $latex {{x}^2}+6x+8=0$.
Solução: Podemos formar uma lista com os fatores de 8: 1×8, 2×4.
Temos que encontrar os fatores que têm uma soma de 6 e um produto de 8:
1+8≠6
2+4=6
Podemos verificar esses fatores usando a propriedade distributiva:
$$(x+2)(x+4)={{x}^2}+2x+4x+8$$
$latex ={{x}^2}+6x+8$
Então, já fatoramos na equação:
$latex (x+2)(x+4)=0$
Agora, resolvemos para cada fator:
⇒ $latex (x+2)=0$ e $latex (x+4)=0$
⇒ $latex x=-2$ e $latex x=-4$
EXEMPLO 2
Resolva a equação $latex {{x}^2}+8x+15=0$ usando fatoração.
Solução: Os fatores com um produto de 15 e uma soma de 8 são:
3×5=15 e 3+5=8
Usamos a propriedade distributiva para verificar:
$$(x+3)(x+5)={{x}^2}+3x+5x+15$$
$latex ={{x}^2}+8x+15$
A equação fatorada é:
$latex (x+3)(x+5)=0$
Resolvemos cada fator:
⇒ $latex (x+3)=0$ e $latex (x+5)=0$
⇒ $latex x=-3$ e $latex x=-5$
Segundo caso: Quando b é positivo e c é negativo
EXEMPLO
Resolva a equação $latex {{x}^2}+6x-7=0$ fatorando.
Solução: Os fatores de -7 são: -1×7, 1×-7.
Encontramos os fatores com um produto de -7 e uma soma de 6:
-1+7=6
1-7≠6
Verificamos com a propriedade distributiva:
$$(x-1)(x+7)={{x}^2}-x+7x-7$$
$latex ={{x}^2}+6x-7$
Já obtivemos a fatoração da equação:
$latex (x-1)(x+7)=0$
Resolvemos para cada fator:
⇒ $latex (x-1)=0$ e $latex (x+7)=0$
⇒ $latex x=1$ e $latex x=-7$
Terceiro caso: Quando b e c são negativos
EXEMPLO
Fatore e resolva a equação $latex {{x}^2}-3x-10=0$.
Solução: Os fatores de -10 são: -1×10, 1×-10, -2×5, 2×-5.
Identificamos os fatores que produzem um produto de -10 e uma soma de -3::
2-5=-3
Usando a propriedade distributiva, podemos verificar os fatores:
$$(x+2)(x-5)={{x}^2}+2x-5x-10$$
$latex ={{x}^2}-3x-10$
Então, a fatoração da equação é:
$latex (x+2)(x-5)=0$
Resolvemos para cada fator:
⇒ $latex (x+2)=0$ e $latex (x-5)=0$
⇒ $latex x=-2$ e $latex x=5$
Quarto caso: Quando b é negativo e c é positivo
EXEMPLO
Resolva a equação $latex {{x}^2}-9x+14=0$ fatorando.
Solução: Começamos encontrando os fatores de 14: -1×-14, -2×-7.
Os fatores com um produto de 14 e uma soma de -9 são:
-2-7=-9
-1-14≠-9
Verificando com a propriedade distributiva, temos:
$$(x-2)(x-7)={{x}^2}-2x-7x+14$$
$latex ={{x}^2}-9x+14$
A fatoração é:
$latex (x-2)(x-7)=0$
Resolvendo para cada fator, temos:
⇒ $latex (x-2)=0$ e $latex (x-7)=0$
⇒ $latex x=2$ e $latex x=7$
Fatorando equações quadráticas quando o coeficiente de x² é maior que 1
Os métodos que acabamos de ver não funcionam quando o coeficiente líder é diferente de 1. Para esses casos. temos que levar em consideração o coeficiente de $latex {{x}^2}$ e os fatores de c para encontrar números que têm uma soma igual a b.
EXEMPLO 1
Resolva a equação $latex 2{{x}^2}-16x+30=0$ por fatoração.
Solução: Temos que determinar se existem fatores comuns na expressão. Neste caso, podemos extrair os 2:
⇒ $latex 2({{x}^2}-8x+15)=0$
Podemos fatorar para $latex ({{x}^2}-8x+15)$. Os fatores de 15 são: -1×-15 , -3×-5.
Determinamos quais fatores produzem uma soma de -8:
-3-5=-8
-1-15≠-8
Usamos a propriedade distributiva para verificar:
$$2(x-3)(x-5)=2({{x}^2}-3x-5x+15)$$
$latex =2({{x}^2}-8x+15)$
$latex =2{{x}^2}-16x+30$
A equação fatorada é:
$latex 2(x-3)(x-5)=0$
Resolvemos para cada fator:
⇒ $latex (x-3)=0$ e $latex (x-5)=0$
⇒ $latex x=3$ e $latex x=5$
EXEMPLO 2
Fatore e resolva a equação quadrática $latex 7{{x}^2}+18x+11=0$.
Solução: Temos que encontrar os fatores de 7 e 11:
1×7=7
1×11=11
Agora, usamos a propriedade distributiva para verificar os fatores:
$$(7x+1)(x+11)\ne 7{{x}^2}+18x+11$$
$$(7x+11)(x+1)=7{{x}^2}+18x+11$$
A fatoração da equação quadrática é:
$latex (7x+11)(x+1)=0$
Resolvemos para cada fator:
⇒ $latex (7x+11)=0$ e $latex (x+1)=0$
⇒ $latex x=-\frac{11}{7}$ e $latex x=-1$
EXEMPLO 3
Fatore e resolva a equação $latex 9{{x}^2}+6x+1=0$.
Solução: Seguindo o mesmo processo dos exemplos anteriores, podemos obter a equação fatorada:
$latex (3x+1)(3x+1)=0$
Resolvemos para cada fator:
⇒ $latex (3x+1)=0$ e $latex (3x+1)=0$
⇒ $latex x=-frac{1}{3}$
EXEMPLO 4
Resolva a equação $latex 6{{x}^2}-7x+2=0$ fatorando.
Solução: Neste caso, é conveniente que comecemos separando o meio termo:
$latex 6{{x}^2}-4x-3x+2=0$
Seguindo o mesmo processo dos exercícios anteriores, temos:
$latex 2x(3x-2)-1(3x-2)=0$
$latex (3x-2)(2x-1)=0$
Resolvendo para cada fator, temos:
⇒ $latex (3x-2)=0$ e $latex (2x-1)=0$
⇒ $latex x=\frac{2}{3}$ e $latex x=\frac{1}{2}$
Veja também
Você quer aprender mais sobre fatoração de equações? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
